Dirichlet Process

Dirichlet Process (DP)

• 참고 : https://github.com/aailabkaist/Introduction-to-Artificial-Intelligence-Machine-Learning/tree/master/Week11

1. Dirichlet Distribution

​ Dirichlet Process에 대해 배우기 이전에, Dirichlet Distribution에 대해 알아보자. Dirichlet distribution의 pdf는 다음과 같다.

\[P(x_1,...,x_k \mid \alpha_1,...\alpha_k) = \frac{\Gamma(\sum_{i=1}^{K}\alpha_i)}{\prod_{i=1}^{K}\Gamma(\alpha_i)}x_i^{\alpha_i -1}\]

이 분포는 주로 베이즈 통계에서 주로 prior distribution으로 자주 사용된다. ( ex. LDA ). 해당 분포가 가지는 특징에는 다음과 같은 것들이 있다.

• \[x_1,...x_{K-1} > 0\]
• \[x_1 + ... + x_{K-1} <1\]
• \[\sum_{i=1}^{K}x_i = 1\]
• \[\alpha_i >0\]

2. Conjugate Relationship

​ Dirichlet distribution은 Multinomial distribution과 conjugate한 관계에 있다. 즉, Likelihood가 Multinomial을 따를 때, prior로 Dirichlet를 설정할 경우, posterior도 Dirichlet 분포를 따르게 된다.

• 1 ) likelihood : \(P(D \mid \theta) = \frac{N!}{\prod_i c_i!}\prod_i \theta_i^{c_i}\)
  • \(N\) : 모든 선택의 경우의 수의 총 합 ( \(N = \sum_i c_i\) )
  • \(c_i\) : \(i\)번째 선택의 횟수

• 2 ) prior : \(P(\theta \mid \alpha) = \frac{1}{B(\alpha)}\prod_i\theta_i^{\alpha_i}\)

• 3 ) Posterior : \(P(\theta \mid D,\alpha) \propto \frac{N!}{\prod_i c_i!}\prod_i \theta_i^{c_i} \times \frac{1}{B(\alpha)}\prod_i\theta_i^{\alpha_i} = \frac{1}{B(\alpha+c)}\prod_i \theta_i^{\alpha_i + c_i -1}\)

3. Dirichlet Process

1) Definition

prior를 만들기 위해 자주 사용하는 Dirichlet Process(DP)는 다음의 식으로 정의할 수 있다.

\[G \mid \alpha, H \sim DP(\alpha,H)\]

이는 곧 다음과 같은 식을 의미한다.

\[(G(A_1),...,G(A_r)) \mid \alpha, H \sim Dir(\alpha H(A_1),...\alpha H(A_r))\]

( 여기서 \(H\)는 base distribution, \(\alpha\)는 prior의 강도를 조절하는 concentration parameter이다. )

2. Properties

mean & variance

\[E[G(A)] = H(A)\] \[V[G(A)] = \frac{H(A)(1-H(A))}{\alpha+1}\]

posterior distribution

앞에서 이야기 했듯, Mulinomial distribution과의 conjugate 관계에 의해 posterior를 다음과 같이 정리할 수 있다.

\[(G(A_1),...,G(A_r)) \mid \theta_1,... \theta_n, \alpha, H \sim Dir(\alpha H(A_1),+n_1...\alpha H(A_r)+n_r)\] \[G \mid \theta_1,...,\theta_n,\alpha, H \sim DP(\alpha+n,\frac{\alpha}{\alpha+n}H + \frac{n}{\alpha+n}\frac{\sum_{i=1}^{n}\delta_{\theta_i}}{n})\]

posterior의 base distribution인 \(H \sim DP(\alpha+n,\frac{\alpha}{\alpha+n}H + \frac{n}{\alpha+n}\frac{\sum_{i=1}^{n}\delta_{\theta_i}}{n})\)가 (\(\alpha\)와 \(n\)에 따른) weigted average형태를 띈 것을 확인할 수 있다.

3. Sampling from DP

앞에서 DP의 posterior distribution까지 정의했다. 그렇다면 이제 이로부터 어떻게 sampling을 할 것인가? 즉, DP로부터 distribution \(G\)를 샘플링할 수 있을까, 그리고 이 \(G\)로부터 어떻게 \(\theta_i\)를 뽑아낼 수 있을까?

Multiple Generation schemes (constructions)

\(G\)를 샘플링( 정확히는 generating )하는 데에는 여러 가지 방법들이 있는데, 대표적으로 다음과 같은 방법들이 있다

( distribution을 construct하는 방식 )

• 방법 1 ) Stick Breaking Scheme

( distribution construct 없이 sampling하는 방식 )

• 방법 2 ) Polya Urn Scheme
• 방법 3 ) Chinese Restaurant Process Scheme

1 ) Stick-Breaking Construction

말 그대로, 막대기를 나누고 해당 막대기의 길이를 고려하여 distribution을 세우고 sampling을 하는 방식을 말한다. 아래의 그림을 참고해보자.

https://slideplayer.com/slide/3361285/12/images/9/Stick+Breaking+Construction.jpg

총 길이가 1인 막대기를 \(k\)등분할 것이다. (\(k=1,2,...,\infty\))

각각의 \(k\)개의 막대기가 가지는 길이를 sampling될 확률로써 생각할 것이다. 그러기 위해 우리는 새로운 변수 \(v_k\)를 도입하는데, 이 \(v_k\)는 \(Beta(1,\alpha)\)를 따른다. ( 0 ~ 1 사이의 값을 가진다 )

하지만 샘플링할 대상이 1개라면, 그냥 \(v_k\)를 사용하면 되지만, 2개 이상이 되는 순간 그 둘의 합 (\(v_1 + v_2\))는 1을 넘어가는 문제가 발생한다. 따라서 우리는 새로운 \(\beta_k\)를 도입하고, \(\beta_k\)의 총 합 ( \(\beta_1 + \beta_2 + ...\))이 1이 되도록, \(\beta_k = v_k \prod_{l=1}^{k-1}(1-v_l)\) 로 설정한다. 이에 대한 common notation은 \(\beta \sim GEM(\alpha)\)이다.

지금까지의 내용을 정리하면 다음과 같이 정리할 수 있다.

• \[G \mid \alpha, H \sim DP(\alpha,H)\]
  • \[\beta \sim GEM(\alpha)\]
  • \[G = \sum_{k=1}^{\infty}\beta_k \delta_{\theta_k}\]
  • \[\theta_k \mid H \sim H\]

2 ) Polya Urn Scheme

Polya Urn Scheme은 Stick Breaking Consruction과 다르게, distribution을 구하지 않고서 sampling을 한다.

\[\theta_n \mid \theta_1,...,\theta_{n-1},\alpha, H \sim DP(\alpha+n-1,\frac{\alpha}{\alpha+n}H + \frac{n-1}{\alpha+n-1}\frac{\sum_{i=1}^{n-1}\delta_{\theta_i}}{n-1})\]

위 식에서 \(\sum_{i=1}^{n-1}\delta_{\theta_i}\) 는 \(i\)번째 datapoint를 제외한 나머지 모든 data point가 선택한 값에 대한 \(\delta\)값의 총 합을 의미한다. 이는, (총 \(K\)개의) cluster 관점에서 보면 다음과 같이 \(\sum_{k=1}^{K}N_K \delta_{\theta_k}\)로 나타낼 수도 있다. ( \(N_k\) : \(k\)번째 선택을 한 총 데이터의 수 )

\[\theta_n \mid \theta_1,...,\theta_{n-1},\alpha, H \sim DP(\alpha+n-1,\frac{\alpha}{\alpha+n-1}H + \frac{n-1}{\alpha+n-1}\frac{\sum_{k=1}^{K}N_K \delta_{\theta_k}}{n-1})\]

따라서, \(E[\theta_n \mid \theta_1,...,\theta_{n-1},\alpha,\H] = \frac{\alpha}{\alpha+n-1}H + \frac{\sum_{k=1}^{K}N_K \delta_{\theta_k}}{\alpha+n-1}\) 로 나타낼 수 있고, 이에 착안하여 다음과 같인 Polya Urn Scheme 알고리즘을 생각해낼 수 있다!

• 빈(empty) urn을 만든다
• X : coin toss from \([0, \alpha+n-1]\) 를 반복한다
  • if \(0 \leq X < \alpha\):
    • \(\theta_n \sim H\) 에서 샘플링한 색깔대로 공을 칠하고, urn에 집어 넣는다
  • if \(\alpha \leq X < \alpha +n-1\)
    • urn에서 임의의 공을 꺼낸 뒤, 해당 색과 같은 공을 하나 더 추가하여 2개를 넣는다

3) Chinese Restaurant Process

위 2)의 Polya Urn Scheme과 유사한 방법으로, 중국집에 손님이 들어와서 여러 개의 table 중 특정한 table에 앉는 것에 빗대어 표현한 방법이다.

https://www.researchgate.net/publication/336241112/figure/fig1/AS:809966290104322@1570122420597/Graphical-representation-of-the-Chinese-Restaurant-Process-CRP.ppm

​ 지금 까지 \(N-1\)명의 고객이 중국집에 들어와서 여러(혹은 하나의) 테이블에 자리를 잡았고, \(N\)번째 고객이 들어왔다고 가정하자. 이 고객은, 기존에 있던 \(N-1\)명의 고객이 앉았던 테이블에 같이 앉을 수도 있고, 새로운 테이블을 개척(?)하여 앉을 수도 있다. 이 비유를, \(DP\)의 sampling에 빗대어 표현하면 다음과 같이 나타낼 수 있다.

• 기존의 table \(K\)에 앉을 확률 : \(P(\theta_n \mid \theta_1, ... \theta_n, \alpha) = \frac{N_k}{\alpha+n-1}\)
• 새 table \(K+1\)에 앉을 확률 : \(P(\theta_n \mid \theta_1, ... \theta_n, \alpha) = \frac{\alpha}{\alpha+n-1}\)

4. de Finetti’s Theorem

​ 이 이론에 대해 알기 이전에, exchangeable하다는 개념에 대해 알아야한다. 우리는 joint pdf가 permutation에 invariant하다면, 이 distribution을 exchangeable 하다고 한다. 즉, permuation \(S\)가 있다고 했을 때, \(P(x_1,x_2,...,x_N) = P(X_{S(1)},...,X_{S(N)})\)를 만족하면 이는 exchangeable 하다.

de Finetti’s Theorem

정의 : if \((x_1,...x_2,..)\) are infinitely exhangeable, then the joint probability \(P(x_1,...,x_N)\) has a representation as a mixture,

\[P(x_1,..x_N) = \int(\prod_{i=1}^{N}P(x_i \mid \theta))dP(\theta) = \int P(\theta)(\prod_{i=1}^N P(x_i \mid \theta))d\theta\]

( 어떤 r.v \(\theta\) 가 만약 iid라면, 이는 exchangeable하다. 그 반대는 False! )

​ 앞에서 설명한 Chinese Restaurant Process 또한 exchangeable process이다. Exchangeability가 중요한 이유는, 이것은 Gibbs sampling을 하는데에 있어서 보다 간단한 derivation을 가능하게 하기 때문이다.

5. DPMM ( Dirichlet Process Mixture Model )

( 기본적으로 GMM (Gaussian Mixture Model)에 대해 알고있다고 가정한다 )

https://media.graphcms.com/hbNxm4eXTtKKiKO4xWet ( 왼쪽 그림은 indicator representation, 오른쪽 그림은 alternative representation )

Indicator Representation of GMM

• \(x\)가 \(\theta\)와 \(z\)에 의해 형성됨
• 식
  • \(\beta \sim GEM(\gamma)\) ( 위의 Stick-Breaking Construction 참고)
  • \(z_i \sim \beta\) ( Multinomial 분포 )
  • \[\theta_k \sim H(\lambda)\]
  • \[x_i \sim F(\theta_{z_i})\]

Alternative Representation of GMM

( 위의 \(\theta\)와 \(z\)를 합쳐서 하나의 \(\theta'\)로 표현한다 )

• \(x\)가 \(\theta'\)에 의해 형성됨

• 식

  • \[G_0 \sim DP(\gamma, H)\]
  • \(\theta_i' \sim G_0\) ( \(\theta_n \mid \theta_1,...,\theta_{n-1},\gamma, H \sim DP(\gamma+n-1,\frac{\gamma}{\gamma+n-1}H + \frac{n-1}{\gamma+n-1}\frac{\sum_{k=1}^{K}N_K \delta_{\theta_k}}{n-1})\) )
  • \[x_i \sim F(\theta_i')\]

Implementation of DPMM

다음과 같은 방법으로 \(\theta'\)를 지속적으로 update할 것이다. ( Alternative Representation 표기를 사용할 것 )

• \[G_0 \sim DP(\gamma, H)\]

• \(\theta_i' \sim G_0\) ( \(\theta_n \mid \theta_1,...,\theta_{n-1},\gamma, H \sim DP(\gamma+n-1,\frac{\gamma}{\gamma+n-1}H + \frac{n-1}{\gamma+n-1}\frac{\sum_{k=1}^{K}N_K \delta_{\theta_k}}{n-1})\) )

• \[x_i \sim F(\theta_i')\]

  ( \(F(x_i \mid \theta_i') = N(x_i \mid \mu_{\theta_i'}, \Sigma_{\theta_i'})\) )

DPMM

• Table을 (랜덤하게) 초기화한다 ( N개의 data에 대하여 \(\theta'\)를 초기화 한다 )
• [Gibbs Sampling] Iterate :
  • dataset의 모든 data에 대하여 :
    • 해당 데이터를 assignment에서 제거한다
    • prior를 계산한다 : \(\theta_n \mid \theta_1,...\theta_{n-1},\gamma,H \sim DP\) ( 여기서 de Finetti’s Theorem이 적용된다. 순서 상관 X )
    • likelihood를 계산한다 : \(N(x_i \mid \mu_{\theta_i'},\Sigma_{\theta_i'} )\)
    • posterior를 계산한다 ( \(\propto\) prior \(\times\) likelihood )
    • posterior로부터 cluster assignment를 샘플링한다
    • parameter를 업데이트한다

​ 위의 과정을 통해 DPMM에서 sampling을 하고 각 데이터에 cluster를 assign해준다. 우리는 여기서 cluster의 개수인 K를 따로 지정해줄 필요는 없다. 하지만, \(\gamma\)를 조정함으로써 개수에 영향을 미칠 수 있다. \(\gamma\)가 클 경우, 더 많은 cluster가 생성되게 된다. ( 앞에서 배운 것을 생각해보자. 새로운 table에 앉을 확률 (혹은 새로운 색깔의 공을 urn에 넣게 될 확률)은 \(\frac{\gamma}{\alpha+n-1}\) 이다 )

6. Hierarchical Dirichlet Process (HDP)

앞에서 GMM을 활용하여 DPMM에 대해서 알아봤었다. 하지만 이것이 꼭 Gaussian말고도 다양한 방법을 사용할 수 있고, 그러기 위해서 Hierarchical Dirichlet Process를 사용할 수 있다.

우리가 가지는 많은 데이터들은 구조화(structured)되어 있다. 예시로, LDA에서 알아본 text data같은 경우에도 corpus-document-..등의 구조가 있다. 우리는 \(x\)를 생성해내는 다양한 \(\theta\)들 (\(\theta_1\), \(\theta_2\),… )등을 서로 어떻게 correlate시킬지에 대해 한번 생각해볼 수 있다.

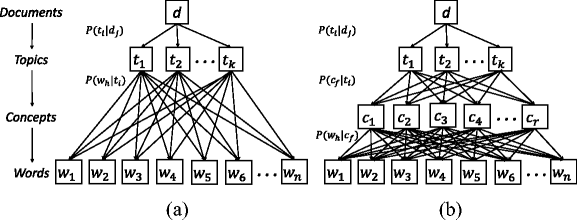
https://media.springernature.com/lw785/springer-static/image/art%3A10.1007%2Fs11042-017-5145-4/MediaObjects/11042_2017_5145_Fig1_HTML.gif

( ex. LDA의 hierarchical 구조 )

1) Hierarchical structure of DP

​ DPMM와의 차이점으로, HDP에서는 \(\theta_i\)가 바로 \(G_0\)에서 샘플링 되는 것이 아니라, \(G_0\)와 \(\alpha_0\)에 의해 sampling 된 새로운 \(G_i\)에서 샘플링된다는 점이다. Chinese Restaurant에 비유하자면, DPMM ( \(G_0\)에서 바로 \(\theta_i\)를 바로 샘플링 )은 “어느 테이블에 앉을 것이냐”를 의미하고, HDP ( \(G_0\)와 \(\alpha_0\)에 의해 \(G_i\)를 결정 짓고, \(G_i\)가 \(\theta_i\)를 샘플링 )은 “어느 테이블에 앉고, 어떠한 메뉴를 주문할 것이냐”를 의미한다고 생각할 수 있다. \(G_0\)를 결정 짓는 파라미터 중 하나인 \(\gamma\)는 “얼마나 다양한 메뉴”를 준비할거냐에 관한 것이고, \(G_i\)를 결정 짓는 \(\alpha_0\)는 “얼마나 다양한 테이블”을 펼 것인지를 나타낸다.

• \(H\) : continuous base distribution
• \(G_0\) : \(G_0 \sim DP(H,\gamma)\)
• \(G_i\) : \(G_i \sim DP(G_0,\alpha_0)\)
  ( 여기서 \(G_0\)는 discrete distribution이다. 따라서 \(G_i\)는 결국 \(G_0\)내에 있는 샘플들에서만 샘플링 될 것이다 )

위 내용을 그림으로 나타내면 아래와 같다.

https://www.researchgate.net/profile/Joan_Capdevila2/publication/301659300/figure/fig1/AS:613886738837507@1523373412115/Hierarchical-Dirichlet-Process-HDP-graphical-model.png

2) Stick Breaking Construction of HDP

• \[G_0 = \sum_{k=1}^{\infty}\beta_k \delta_{\phi_k}\]
  • \[\phi_k \sim H\]
  • \[\beta_k = \beta'_k \prod_{l=1}^{k-1}(1-\beta'_l)\]
    • \[\beta_k' \mid \gamma \sim Beta(1,\gamma)\]
• \[G_i = \sum_{k=1}^{\infty}\pi_{ik}\delta_{\phi_k}\]
  • \[\pi_{ik} = \pi_{ik}' \prod_{l=1}^{k-1}(1-\pi_{il}')\]
  • \[\pi_{ik}' \mid \gamma \sim Beta(\alpha_0 \beta_k, \alpha_0(1-\sum_{i=1}^{k}\beta_i))\]