Gumbel-Softmax Trick

1. Reparameterization Trick

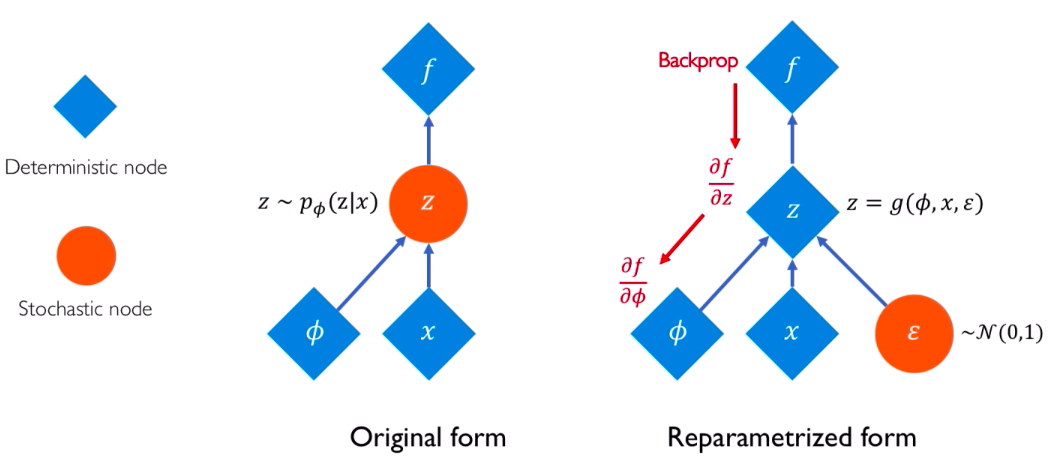
세 줄 요약 :

stochastic term을, 두 개의 부분 (1) stochastic & (2) deterministic으로 나누는 과정
나누는 이유? Back Propagation을 하기 위해

( stochastic한 부분에 대해서는 back-propagation을 할 수 없다. 따라서 deterministic한 부분을 만들어주고, 이에 대해 back-prop을 실시한다. )
ex) \(x \sim N(\mu_{\phi}, \sigma^2_{\phi})\)
- stochastic 부분 : \(\epsilon \sim N(0,1)\)
- 따라서, \(x = \mu_{\phi} + \sigma^2_{\phi}\cdot \epsilon\)

Categorical Variable을 reparameterization하는 대표적인 두 가지 방법으로

다음과 같이 Categorical 분포를 따르는 \(z\)가 있다고 해보자.

\[z \sim \text{Categorical}(\pi_1,...,\pi_k)\]

이때, 우리는 \(z\)를 다음과 같은 방법으로 샘플링할 수 있다.

\(z = \underset{k}{\text{argmin}} \frac{\xi_k}{\pi_k}\), where \(\xi_k \sim \text{Exp}(1)\)

( 혹은, \(z = \underset{k}{\text{argmax}} \frac{\pi_k}{\xi_k}\))

( \(\pi_k\)가 클 수록, 즉 높은 확률일 수록 더 샘플링 될 확률이 높아지는 꼴이다.)

위 식에 log를 씌우면, 다음과 같이 정리될 수 있다.

\[z = \underset{k}{\text{argmax}} [log\pi_k - log\xi_k]\]

( 여기서 \(-log\xi_k\)가 Gubmel(0,1) 분포를 따르기 때문에 해당 방법의 이름이 Gumbel-Max trick이다 )

우리는 위 방법을 통해 stochastic 부분과 deterministic 부분으로 바꾸는 reparameterization을 했다. 하지만, 이는 여전히 argmin/argmax의 특성 상 해당 경계를 제외하고 \(\pi\)에 대한 미분이 불가능(0이 된다)하다.

따라서 우리는 이를 continous하게 만들어 줄 필요가 있고, 그래서 등장한 것이 Gumbel-Softmax Trick이다.

생각보다 간단하다. Gumbel-max Trick에서 argmax를 softmax로만 바꿔주면 된다.

우선 softmax함수에 대한 식을 정리하면 다음과 같다.

\[\text{softmax}_{\tau}(x)_j=\frac{exp(x_j / \tau)}{\sum_{k=1}^{K}exp(x_k / \tau)}\]

여기서 \(\tau\)는 위 softmax의 ‘sharpness’를 결정한다

지금까지 \(z\)는 one-hot vector로, discrete했다. 우리는 이를 다음과 같이 softmax를 사용하여 continuous하게 변형할 것이고, 이를 \(\tilde{z}\) 로 나타낼 것이다.

\[\tilde{z}(\gamma, \pi) := \text{softmax}_{\tau}(log\pi_1 + \gamma_1, .... , log\pi_k + \gamma_k)\]

\[\gamma_k \sim \text{Gumbel}(0,1)\]
- \[\gamma_k = -log(-logu_k)\]
- \[u_k \sim \text{Uniform}(0,1)\]

\(\tau\)값을 어떻게 설정하냐에 따라 sample 및 expectation은 다음과 같이 변한다. ( 여기서 \(\tau\)를 temperature라고 부른다 )

expectation : \(\underset{q_{\phi}(z)}{E}f(z) \approx\underset{q_{\phi}(\tilde{z})}{E}f(\tilde{z}) = \underset{p(\gamma)}{E}f(\tilde{z}(\gamma, \phi))\)
gradient : \(\frac{\partial}{\partial \phi}f(\tilde{z}(\gamma, \pi(\phi)))\)