Jackknife & Bootstrapping [2]
참고 자료 : 임종호 교수님 수리통계학2 강의 자료
앞에 포스트(Jackknife)에 이어서, 이번에는 Bootstrapping에 관한 내용을 다룰 것이다.
3. Bootstrapping
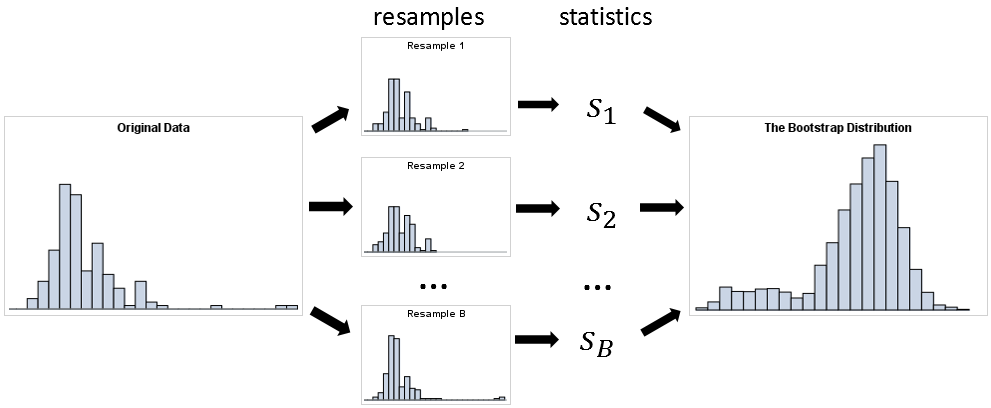
( 출처 : https://blogs.sas.com/content/iml/files/2018/12/bootstrapSummary.png )
한 문장으로 요약하면, 여러번의 resample을 통해, 각각으로부터 statistic을 구해내고, 이 statistic들의 분포를 통해 원래 데이터의 분포를 유추하는 것이다.
여러가지 Bootstrapping 방법이 있는데, 대표적인 두 가지 방법에 대해 소개하겠다.
1) Boostrap Procedure
\(X_1,...X_n \overset{iid}{\sim} F(x)\) and \(T_n =T_n(X_1,...,X_n)\)
[ STEP 1 ] 위의 \(F(x)\)에서 random sample 한 \(\{X_1,...,X_n\}\) 에서, 중복을 허용하여 \(X_1^{*},...,X_n^{*}\)을 sampling한다
[ STEP 2 ] Step 1에서 뽑은 (b-th) sample들을 통해 \(T_{n}^{*(b)}\)를 계산한다
[ STEP 3 ] Step1 & Step2를 B번 반복하여, \(T_n\)에 대한 bootstrap distribution을 구한다
\(T_n\)의 variance는 \(\{T_n^{*(b)}\}_{b=1}^{B}\)의 sample variance를 통해 estimate할 수 있다.
\[\hat{\sigma}^2_{boot} = \frac{1}{B-1}\sum_{b=1}^{B}(T_n^{*(b)}-T_n^{*})^2\]where \(T_n^{*} = \frac{1}{B}\sum_{b=1}^{B}T_n^{*(b)}\)
2) Parametric Boostrap Procedure
\(X_1,...X_n \overset{iid}{\sim} F(x)\) and \(T_n =T_n(X_1,...,X_n,F(\theta))\)
이 방법은, 위의 1) Bootstrap Procedure와 유사하지만, \(F(x)\)에서 random sample 한 \(\{X_1,...,X_n\}\) 에서 random sample을 뽑는 것이 아니라, \(\{X_1,...,X_n\}\)에서 바로 \(\hat{\theta}\) 를 추정하고, \(F(\hat{\theta})\) 에서 random sample을 뽑는다는 점이 차이점이다.
[ STEP 1 ] \(\{X_1,...,X_n\}\)에서 \(\hat{\theta}\)를 estimate한다
[ STEP 2 ] \(F(\hat{\theta})\) 에서 \(X_1^{*},...,X_n^{*}\)를 sampling한다
[ STEP 3 ] Step 2에서 뽑은 (b-th) sample들을 통해 \(T_{n}^{*(b)}\)를 계산한다
[ STEP 4 ] Step 2 & Step3을 B번 반복하여, \(T_n\)에 대한 bootstrap distribution을 구한다
4. Bootstrap Bias Corrected Estimator
\(T_n\)을 \(\theta(F)\)에 대한 estimator라고 하자.
그러면, \(T_n\)의 bias는 \(E[T_n] - \theta\)로 나타낼 수 있고
\(T_{n}^{*}\) ( Bootstrap Estimate)의 bias는 \(E[T_n^{*}] - \theta(\hat{F})\)로 나타낼 수 있다.
( often, \(\theta(\hat{F}) = T_n\) )
따라서, bias corrected bootstrap estimator는 다음과 같이 구할 수 있다!
\[\begin{align*} T_{n,boot} &= T_n - (\bar{T}_n^{*}-T_n)\\ &= 2T_n - \bar{T}_n^{*} \end{align*}\]