Normalizing Flow
1. VAE 간단 요약
VAE의 E step에서, 우리는 잠재변수에 대한 분포 (\(q(Z)\)) 를 계산해야한다.
이를 factorize하고 Bayes’ rule에 의해 정리하면 다음과 같다.
\[q(Z) = \prod_{i=1}^{n}q(z_i) = \prod_{i=1}^{n}p(z_i \mid x_i, \theta) = \prod_{i=1}^{n}\frac{p(x_i \mid z_i, \theta p(z_i))}{\int p(x_i \mid z_i, \theta) p(z_i)dz_i}\]하지만, 위 식에서 분모는 intractable하기 때문에, 우리는 이를 계산하는 대신, \(p(z_i \mid x_i, \theta)\)를 다음과 같이 근사한다. ( 왜 다음과 같은 식으로 근사를 하는 것이 곧 ELBO를 최소화 하는 것인지는 다음의 블로그 글의 (1) E-step을 참고하길 바란다 : https://seunghan96.github.io/stat/10.-em-EM_algorithm(2)/ )
\[q(z_i \mid x_i , \phi) \approx p(z_i \mid x_i, \theta)\]그리고 VAE에서는, 위의 \(q\)함수를 아래와 같이 다루기 쉬운 여러 개의 Factorized Gaussian의 조합으로 나타낸다.
\[q(z_i \mid x_i, \phi) = \prod_{j=1}^{d} N(z_{ij} \mid \mu_j(x_i), \sigma^2_j(x_i))\]위의 \(z\)에 대한 사후확률분포에서 단순한 Gaussian 분포를 사용하기 때문에, 이를 활용하여 보다 복잡한 형태를 표현하고자 하는 것이 Normalizing Flow (NF)의 취지라고 할 수 있다.
2. Normalizing Flow, NF
위 식에서 \(z\)는 Gaussian 분포 \(q\)에서 뽑힌 값이다. 우리가 \(z\)에 대해서 특정한 형태의 함수를 반복적으로 적용한다면 보다 복잡한 형태의 \(z\)를 만들 수 있을 것이다.
\[z_k = f_k \circ f_{k-1} \circ ... \circ f_2 \circ f_1 (z_0)\]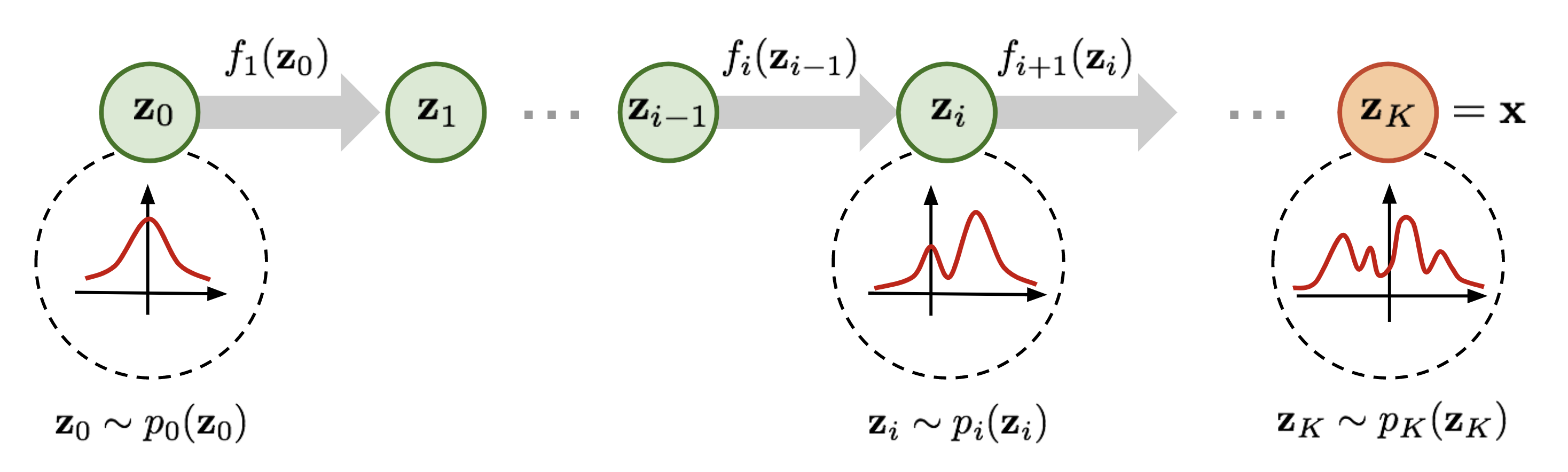
[ 참고 : https://lilianweng.github.io/lil-log/assets/images/normalizing-flow.png ]
매우 복잡한 과정일 것 같지만, 아래와 같은 식을 활용하면 간단하게 나타낼 수 있다.
\[q(z) = q(f(z)) \left \| det \frac{\partial f(z)}{\partial z^T} \right \|\]위 식에 \(log\)를 씌우면 아래와 같다.
\[log q(z) = logq(f(z)) + log \left \| det \frac{\partial f(z)}{\partial z^T} \right \|\]해당 과정을 총 \(k\)번 반복하면, 우리는 다음과 같은 식을 구할 수 있다.
\[logq_k(z) = logq(f_k(z)) + log \left \| det \frac{\partial f_k(z)}{\partial z^T} \right \|= logq(f(z)) + \sum_{i=1}^{k}log \left \| det \frac{\partial f^i}{f^{i-1}} \right \|\]이렇게 해서 계산한 \(logq_k(z) = \sum_{i}logq_k(z_i)\)를 최대화 하는 \(f\)를 찾으면 된다.
3. Determinant term of NF
\(q(z) = q(f(z)) \left \| det \frac{\partial f(z)}{\partial z^T} \right \|\)식에서, 우리는 행렬식(determinant)를 계산해야 하지만, 아래와 같은 특정 형태의 \(f\)를 사용하면 쉽게 행렬식을 계산할 수 있다.

[ 참고 : https://i.imgur.com/DtOLSdZ.png ]
4. VI with Normalizing Flows
해당 NF를 Variational Inference에 적용한 알고리즘은 아래와 같다.

