Uncertainty

Uncertainty

불확실성(Uncertainty)에는 다음과 같이 크게 세 종류의 불확실성이 있다.

• Aleatoric Uncertainty
• Epistemic Uncertainty
• Out-of-Distribution Uncertainty

1. Aleatoric Uncertainty

• 데이터 “생성과정”에서 발생하는 무작위성

• 따라서, 단지 데이터의 수를 늘린다고 해서 줄어드는 불확실성이 아님!

• ex)

  • \(x \sim N(0,1)\)에서 \(x\)를 샘플링한다고 해보자. 여기서 \(x\)를 1개를 뽑든, 999999개를 뽑든,

    해당 \(x\)는 (분산) 1 만큼의 불확실성을 가지고 있다.

데이터를 늘린다고해서 줄일 수 있는 불확실성이 아니라고해서, 무시해되 되는 것은 아니다. 우리는 대신에 해당 aleatoric uncertainty의 정도를 출력해 줄 수 있는 모델을 만드는 것이 중요하다!

2. Epistemic Uncertainty

• “모델”의 불확실성과 관련있는 불확실성

  ( 즉, 우리가 정확한 모델의 파라미터를 모르는 데에서 오는 불확실성이다. )

• 데이터의 수를 늘리면 줄어드는 불확실성!

• ex) (1,2), (4,8) 두 점으로 추정한 간단한 선형회귀식 \(y=\beta x\)에서의 \(\hat{\beta}=2\)

  (1,2),(2,4),(3,6),(4,8)…..(400,800) 400개의 점으로 추정한 간단한 선형회귀식 \(y=Ax\)에서의 \(\hat {\beta}=2\)

  두 결과 모두 \(\beta\)를 2로 예측하였다. 하지만 전자의 경우보다, 후자의 경우가 더욱 더 \(\hat{\beta}\)에 대해 더욱 강하게 확신할 수 있을 것이다. ( 다른 말로, 2개의 점만으로 추정한 \(\hat{\beta}\)는 400개의 점으로 추정한 것보다 더 “불확실하다”라고 할 수 있다. )

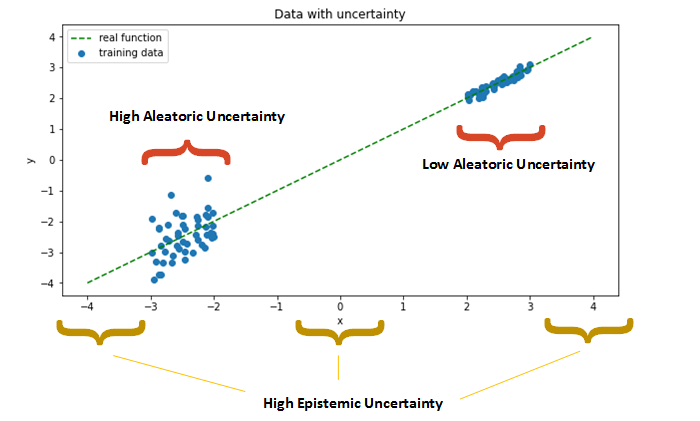
**출처 : Uncertainty in Deep Learning. How To Measure?

Towards Data Science**

3. Out-of-Distribution Uncertainty (OoD)

• 입력 자체가, 우리가 예상했던 분포에서 들어오지 않은 입력값일 때!

• (기본 가정) train & valid & test 데이터는 우리가 다루고자하는 데이터의 모든 범위를 다 커버하고 있다!

  하지만, 이 가정에 어긋나는 데이터, 즉 정말 새로운 분포에서 데이터가 올 경우에 발생하는 문제이다.

• OoD 입력을 처리하는 방법

  • 1) OoD가 모델에 입력 되기 전에 해당 입력을 탐지하기

    ( 즉, 입력이 우리의 train dataset의 분포에 속하는지를 판별한다 ) ( ex. GAN의 Discriminator가 맡게 되는 역할 )

  • 2) OoD의 입력을 받되, 해당 입력의 불확실성에 대해 예측하기

    ( ex. Softmax가 출력하는 값들은 전부 “확률”값으로, 해당 정답에 대한 (불)확실성을 보여준다 )