[multimodal] FE of signal data - (1) Fourier Transform

[ Feature Extraction of signal data ]

Signal data에서 feature를 뽑아내는 대표적인 2가지 방법은 아래와 같다.

• 1) Fourier Transform
• 2) Mel-Frequency Cepstral Coefficients (MFCC)

이번 포스트에서는 우선 Fourier Transform에 대해서 다룰 것이다.

1. Before Fourier Transform….

Fourier Transform : “시간(time)의 영역에서 주파수(frequency)”의 영역으로 변환

( 푸리에 변환은 time(시간) 과 frequency(주파수)의 관점을 전환할 수 있게 해주는 중요한 것 )

보다 직관적인 이해를 위해….

ex) 속도를 “시간”과 “거리”의 관점에서 바라봄

• 100m 달리기를 몇초에 달려? \(\frac{? \text{seconds}}{100\text{ m}}= \frac{ \text{time}}{\text{distance}}\)
• 자동차가 얼마나 빨리 달려? \(\frac{? \text{km}}{1 \text{ hour}} = \frac{ \text{distance}}{\text{time}}\)

위 예시의 두 가지 경우 모두 “속도”에 대해서 이야기하지만, 하나는 “시간”의 관점에서, 하나는 “거리”의 관점에서 바라보았다.

이를 푸리에 변환과 연관시켜 생각해보면 아래와 같다.

• (time 영역) cycle이 얼마나 빨리 일어나?

  • \(\frac{ \text{time}}{\text{cycle}}\)= Period

• (frequency 영역) 1초 동안 cycle이 얼마나 자주 일어나?

  • \(\frac{ \text{cycle}}{\text{time (1s)}}\)= Hz

  
  

푸리에 변환을 통해서 알고자 하는 것을 쉽게 비유해서 설명하자면,

여러 과일이 섞여있는 스무디의 “과일의 구성 성분을 알려주는 것”이라고 보면 된다.

( ex 스무디 A = 딸기 30% + 바나나 50% + 사과 20% )

2. Introduction

푸리에 변환을 알기 위해서는 아래의 4가지 사항들에 대해서 잘 알아야 한다.

• 1) 푸리에 급수 (Fourier Series) : cos & sin을 엄청 많이 사용해서 어떠한 것을 만들까?
• 2) 오일리 공식 (Euler formula) : cos & sin을 “하나”로 표현해줌!
• 3) 적분 (Integration) : 리만 적분
• 4) 직교성 (Orthogonality) : 벡터의 내적이 아니라, “함수의 내적”!

\(\rightarrow\) “시간의 영역”에 있는 데이터를 “주파수의 영역”에 있는 영역으로 어떻게 옮길 수 있는지?

2-1. Fourier Series

아래의 식은 Foureir Seires(푸리에 급수)이다.

\[\hat{f}(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos \left(\frac{2 \pi n x}{T}\right)+\sum_{n=1}^{\infty} b_{n} \sin \left(\frac{2 \pi n x}{T}\right)\]

위 식이 담고 있는 의미를 알아보자.

• [Point 1] cos & sin을 무한히 사용해서 “주기성 함수”를 표현할 수 있다!

• [Point 2] 직류 & 교류

  • 직류(DC)를 나타내는 term : \(\frac{a_{0}}{2}\)
    • 주기성 함수를 위/아래로 옮기는 상수
  • 교류(AC)를 나타내는 term : \(\sum_{n=1}^{\infty} a_{n} \cos \left(\frac{2 \pi n x}{T}\right)+\sum_{n=1}^{\infty} b_{n} \sin \left(\frac{2 \pi n x}{T}\right)\) (반복을 하는 주기성을 가짐)
    • 주기는 sin & cos를 섞어서(혹은 하나만 사용하여) 나타낼 수 있다!

  .

• [Point 3] Noise처럼 보이는 어떠한 함수도 Fourier Series로 나타낼 수 있다!

2-2. Euler formula

아래는 식은 Euler Formula (오일러 공식)이다.

\[e^{+i \omega t}=\cos (\omega t)+i \sin (\omega t)\]

위 식이 담고 있는 의미를 알아보자.

• [Point 1] cos & sin을 하나로 나타내줌 ( using 지수 함수 )

• [Point 2] 오일러 공식이 왜 중요한가?

  

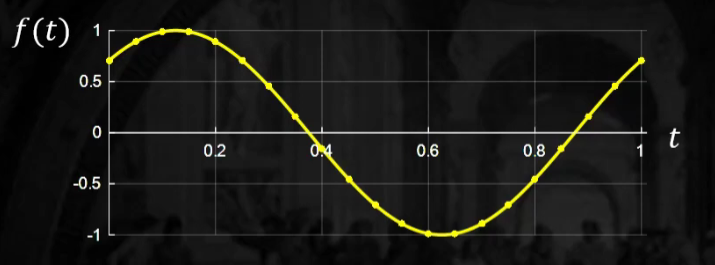
  • Sine 함수

    • 기본 sine 함수 ) \(f(t)=1 * \sin (2 \pi * t)\)

    • 위의 그림처럼 해주기 위해서는….

      ( 위상 + ) \(f(t)=1 * \sin (2 \pi *(t+\varphi))\)

      ( 왼쪽으로 움직임 , where \(\varphi>0\) )

  • Cosine 함수

    • 기본 coinse 함수 ) \(f(t)=1 * \cos (2 \pi *t)\)

    • 위의 그림처럼 해주기 위해서는….

      ( 위상 - ) \(f(t)=1 * \cos (2 \pi *(t-\varphi>0))\)

      ( 오른쪽으로 움직임, where \(\varphi>0\) )

  • 위상을 사용하지 않아도 되는 방법?

    (1) cosine & sine을 섞어서 사용하기

    • \(f(t)=\frac{\sqrt{2}}{2} \sin (2 \pi * t)+\frac{\sqrt{2}}{2} \cos (2 \pi * t)\).

    (2) Euler 함수 사용하기

    • \(f(t)=1 * e^{i 2 \pi *(t-0.125)}\).
    • 물리적으로 의미가 있는 부분을 가져오기 위해서는 “실수”부분을 가져오면 된다!

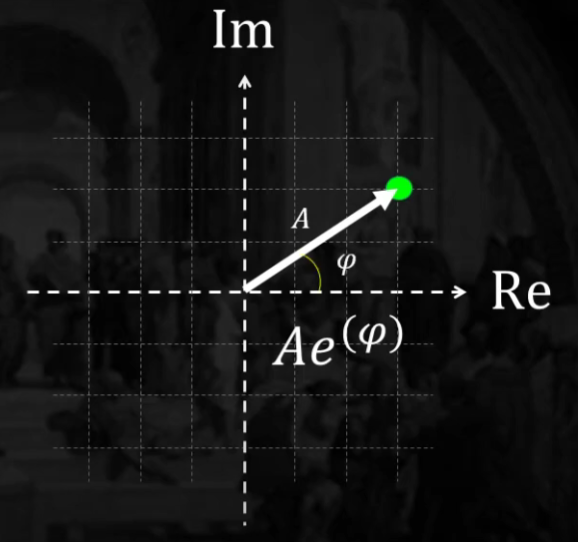
• [Point 3] 따라서, 아래의 오일러 함수로 어떠한 주기성 함수도 표현할 수 있다

  • \(f(t)=A * e^{i 2 \pi f *(t-\varphi)}\).
    • \(A\) : 진폭
    • \(f\) : 주파수
    • \(\varphi\) : 위상

• [Point 4] 오일러 함수가 Fourier Transform에서 유용한 또 다른 이유? “지수 함수”

  • 미분/적분해도 지수 함수!

• [Point 5] sine & cosine을 복소수 함수로 표현한다는 의미?

  

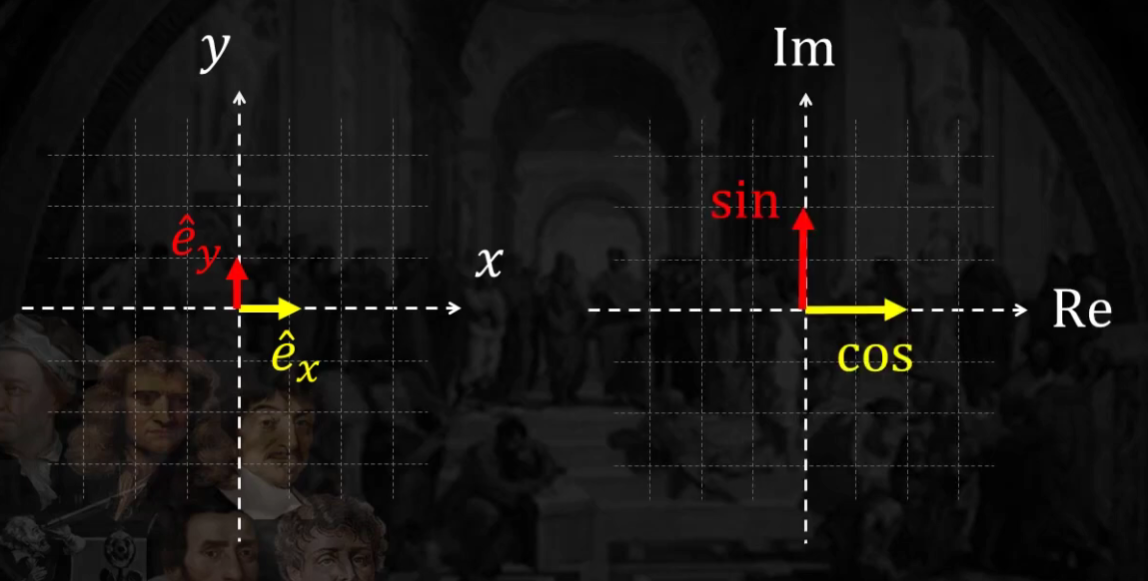
  • 실수 부분은 cosine, 허수 부분은 sine으로 표현

  • 즉, 어떠한 주기성 함수를 cosine & sine의 섞음으로 나타낼 수 있다!

    

2-3. Integration

SKIP

2-4. Orthogonality

우리에게 친숙한 벡터간의 직교성말고, 함수의 직교성에 대해서 알아볼 것이다. ( 그 직관은 크게 다르지 않다 )

내적을 구한다 = “연관성을 찾는다”

• 0 : 연관성 X
• 1 / -1 : 정/반대의 연관성 O

“함수”의 내적 & 직교성?

• 함수의 내적 : \(\langle\hat{f}, \hat{g}\rangle=\int f(t) g(t) d t\)

그림으로 이해하기

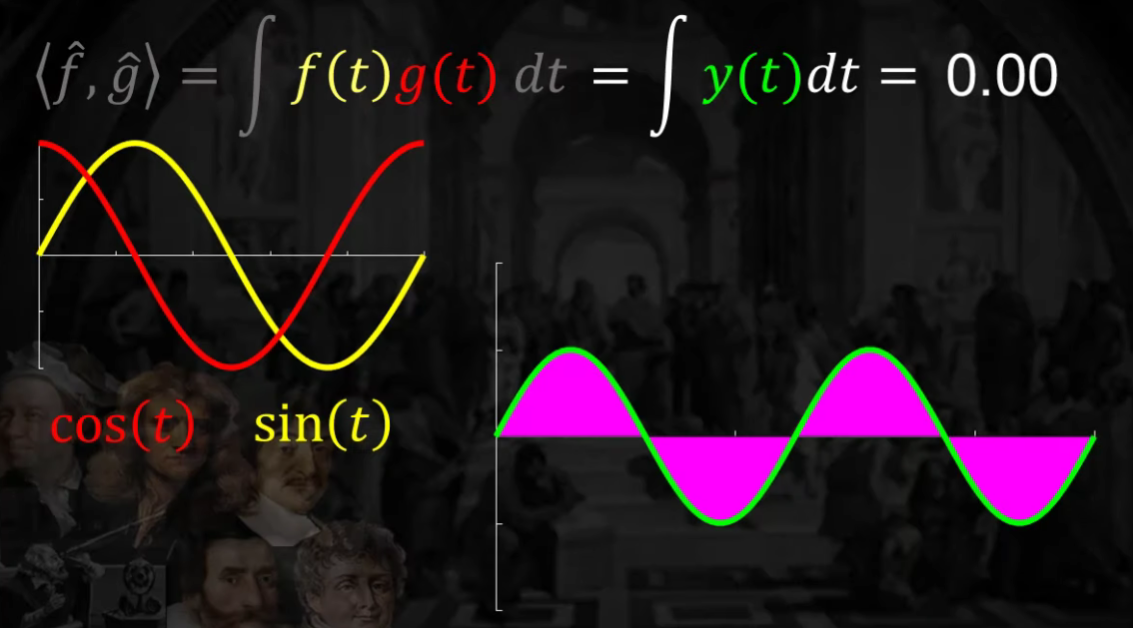
• cosine과 sine이 직교(서로 연관성 X)하는 그림

• \(\langle\hat{f}, \hat{g}\rangle=\int \sin (t) \cos (t) d t=0\).

  • 왜 0이라는 사실이 중요한가?

    기저벡터 2개가 연관성이 서로 없기 때문에 모든 좌표축의 벡터를 설명할 수 있는 것처럼,

    cosine & sine도 마찬가지로 그러한 역할을 할 수 있다! 즉, 어떠한 주기성 함수도 설명할 수 있다!

2-5. Foureir Transform Example

오일러 공식을 사용하여 전개해보면…

\[\begin{array}{l} \hat{f}(\omega)=\int_{-\infty}^{\infty} f(t) e^{i \omega t} d t \\ \hat{f}(\omega)=\int_{-\infty}^{\infty} f(t)[\cos (\omega t)+i \sin (\omega t)] d t \\ \hat{f}(\omega)=\int_{-\infty}^{\infty} f(t) \cos (\omega t) d t+i \int_{-\infty}^{\infty} f(t) \sin (\omega t) d t \end{array}\]

위의 식에서, 우선 sine함수만 사용하여 변환을 해볼 것이다. ( \(\int_{-\infty}^{\infty} f(t) \sin (\omega t) d t\) )

[ Example ]

\(F_1(t)\) 와 같은 data가 있다고 해보자. 이 data에 어떠한 주기성이 있는지를 알아보고자 한다.

그 기준점이 될 함수로 \(sin(2\pi \cdot f \cdot t)\)를 사용할 것이다. ( \(f\) : 주파수 )

주파수로 \(f=1\)을 놓을 것이다.

이 두 함수 ( \(F_1(t)\) 와 \(sin(2\pi \cdot 1 \cdot t)\) )를 곱한 뒤, 적분을 하는 것은, 이 두 함수 사이의 연관성을 찾는 것을 의미한다. 그 값은 0이 된다 ( when \(f=1\) )

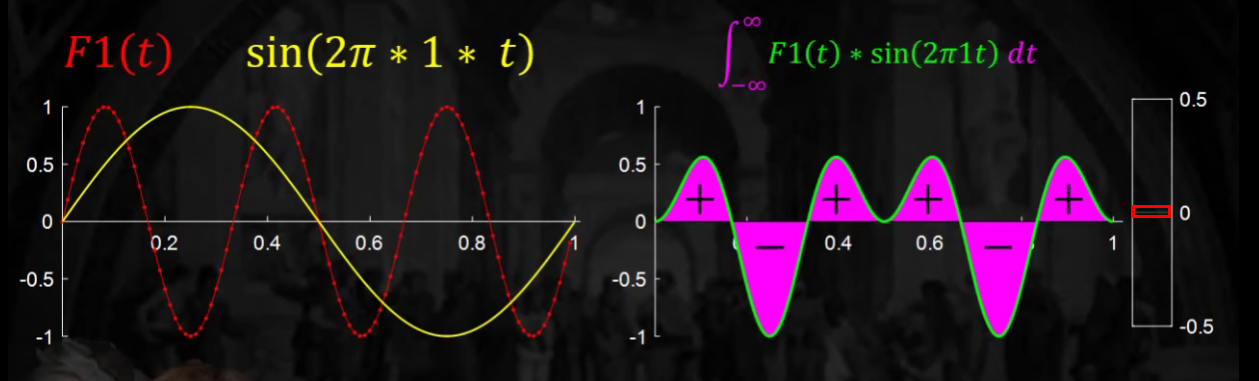
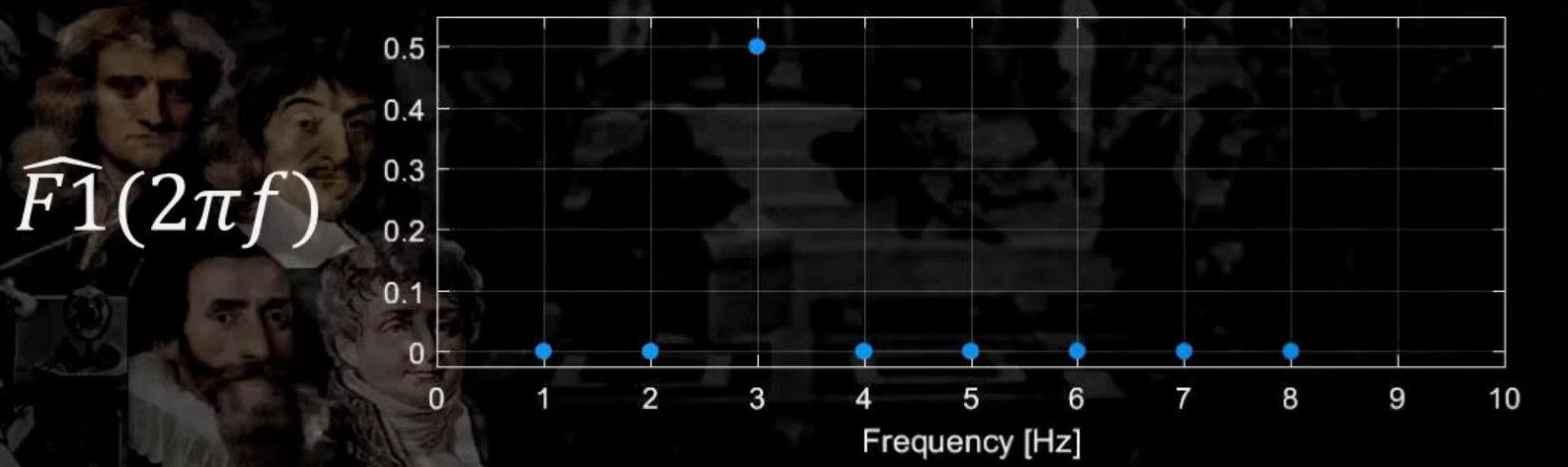
이와 같이, 주파수(\(f\) )를 늘려감에 따라 그 결과값을 아래와 같이 기록해갈 것이다.

이번엔, sine 함수 두개를 1 & 0.5 만큼 섞어서 나타내본 결과이다.

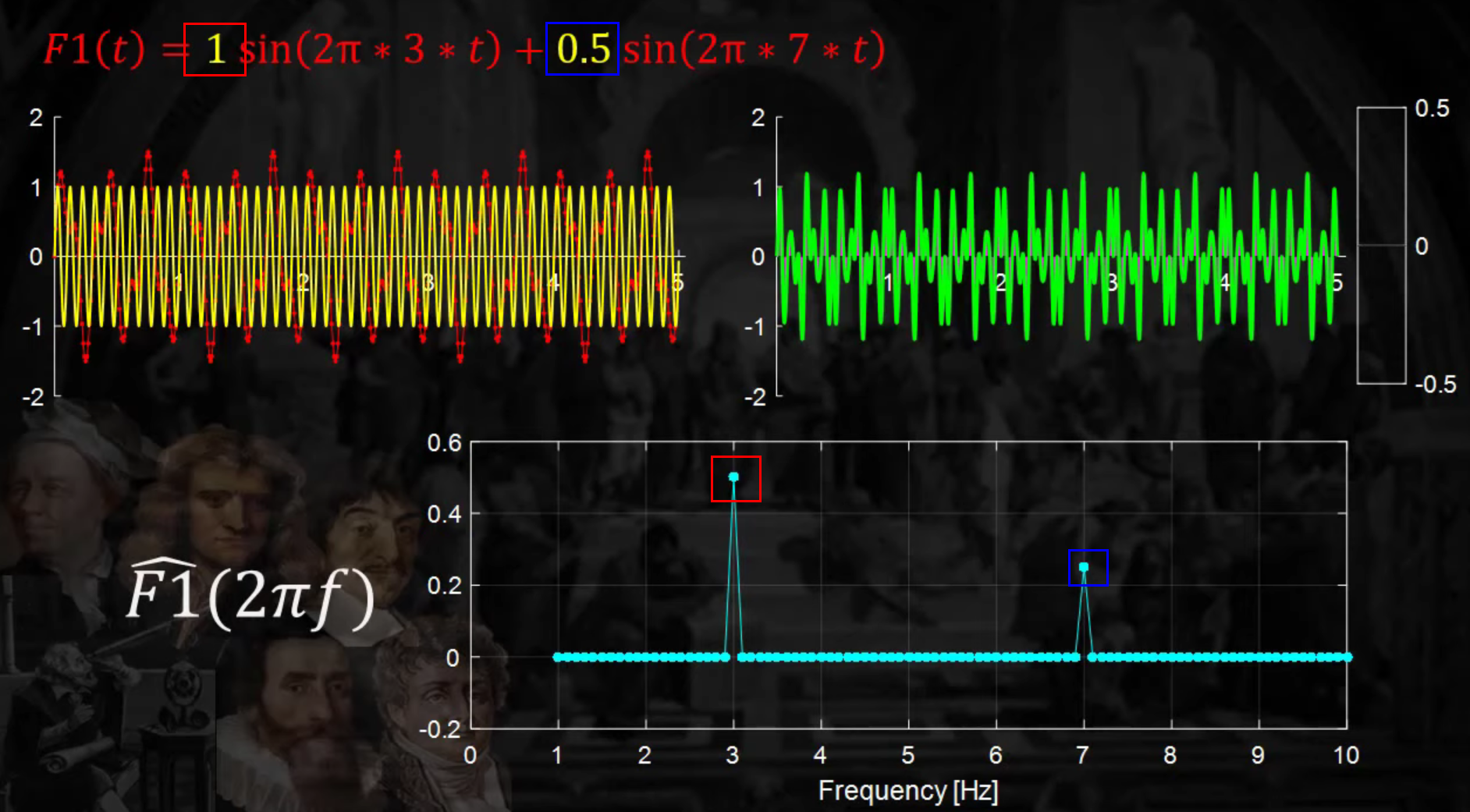
• (빨간색) 계수 : 1 , 변환 결과값 : 0.5
• (파란색) 계수 : 0.5, 변환 결과값 : 0.25
  • 절반밖에 캐치 못한 이유는? “cosine도 사용해야!”

따라서, sine & cosine 두 개를 섞어서 사용하면 아래와 같다.

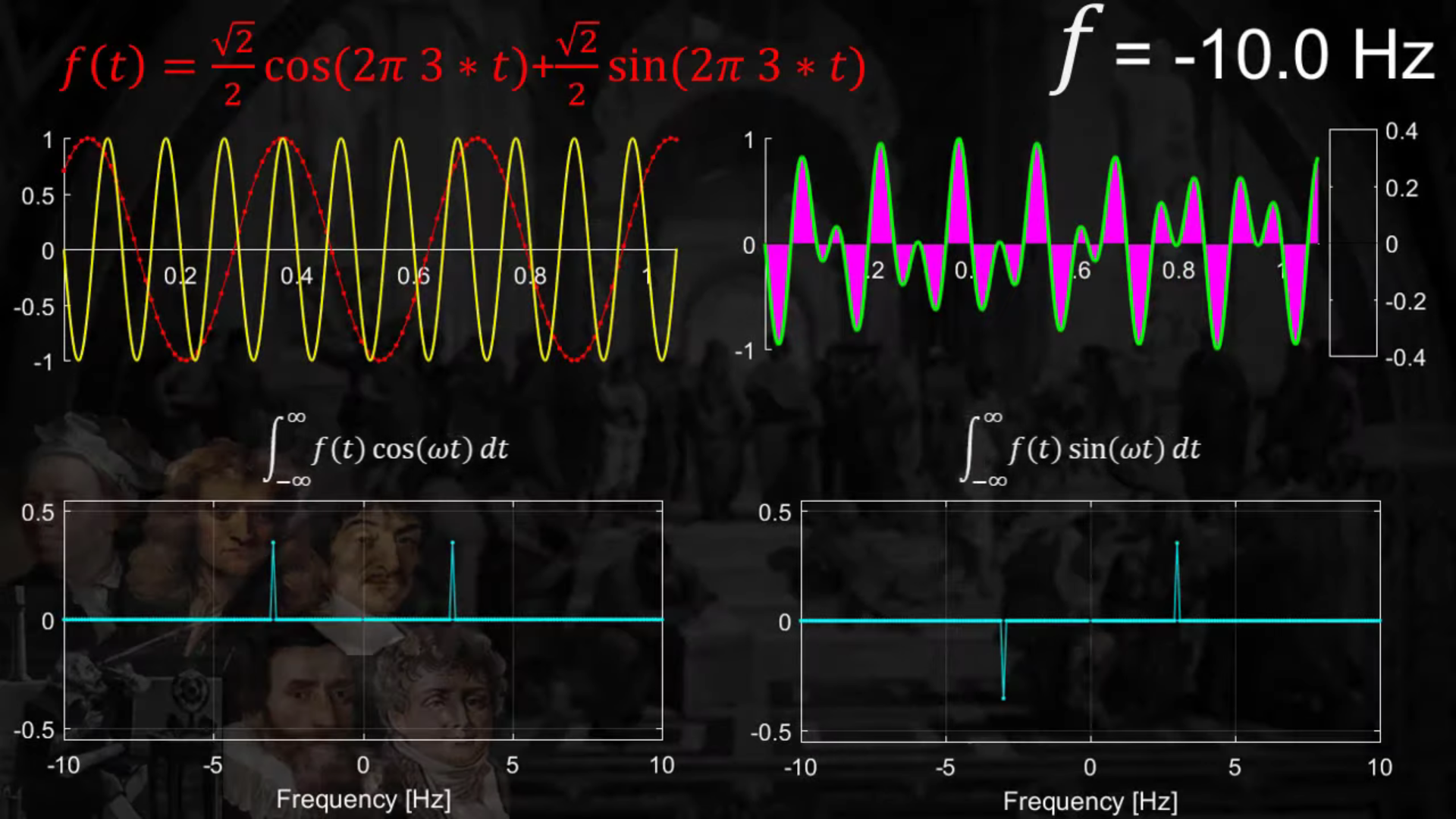
하지만 위 처럼 sine과 cosine을 따로따로 하지 않고, “오일러 공식”을 사용해서 한번에 할 수 있다!

• (before) \(\int_{-\infty}^{\infty} f(t) \cos (\omega t) d t, \quad \int_{-\infty}^{\infty} f(t) \sin (\omega t) d t\)
• (after) \(\int_{-\infty}^{\infty} f(t) * e^{i \omega t} d t\)

3. Fourier Transform 요약

( 앞으로 다룰 Fourier Transforms는 전부 DISCRETE Fourier Transform )

• time에 대한 함수 & frequency에 대한 함수를 연결해줌
• 특정 domain ( time or frequency )의 signal \(\rightarrow\) 특정 domain ( time or frequency )의 signal
• 용어 : Fourier Transform \(\leftrightarrow\) Inverse Fourier Transform
• 공식 :
  • Fourier Transform : \(X_k =\sum_{n=0}^{N-1}x_n \cdot e^{\frac{-i 2\pi k n}{N}}\)
  • Inverse Fourier Transform : \(x_n =\frac{1}{N}\sum_{k=0}^{N-1}X_k \cdot e^{\frac{-i 2\pi k n}{N}}\)

.

Euler’s formula (오일러 공식)

• 삼각함수 & 지수함수에 대한 관계
• 공식 : \(\exp(i \theta)= \text{cos} \theta + i\cdot \text{sin} \theta\)
  • 실수 part) \(\text{cos} \theta\)
  • 허수 part) \(i\cdot \text{sin} \theta\)
• 오일러 등식 ( 위의 식에 \(\theta=\pi\) 대입 )
  • \(\exp(i \theta)+1=0\).
• 복소 지수 함수 : \(cis(\theta) =\exp(i \theta)= \text{cos} \theta + i\cdot \text{sin} \theta\)
• 의미?
  • \(\exp(i \theta)\) : 복소 평면 상 반지름이 1인 원

.

Fourier Transform 공식 들여다보기

(Discrete) Fourier Transform : \(X_k =\sum_{n=0}^{N-1}x_n \cdot e^{\frac{-i 2\pi k n}{N}}\)

( 가정 : time \(\rightarrow\) frequency )

• \(n\) : time index

• \(x_n\) : time 도메인에서의 \(n\)번째 샘플

• \(X_k\) : frequency 도메인에서의 \(k\)번째 Fourier Transform 결과

• \(\frac{k}{N}\) : 각 속도 (angular velocity)

  ( 즉, 단위원이 얼마나 빠르게 회전하는지 )

(해석) \(X_k\) : time 도메인 신호에서 \(k/N\) 에 해당하는 주파수 성분

(Discrete) Fourier Transform 공식을 복소 지수 함수를 사용하여 다시 나타내기

\(\begin{aligned} X_k &=\sum_{n=0}^{N-1}x_n \cdot e^{\frac{-i 2\pi k n}{N}} \\ &=\sum_{n=0}^{N-1}x_n \cdot [\text{cos}(\frac{2\pi}{N}kn) - i \cdot \text{sin}(\frac{2\pi}{N}kn)]\end{aligned}\).

4. DFT Matrix

• Discrete Fourier Transform (DFT)를 matrix 형태로 나타낸 것
• 일종의 선형 변환으로 볼 수 있음 ( \(\vec{X}=W \cdot \vec{x}\) )
• notation
  • \(x\) : time 도메인의 signal
  • \(W\) : \(N \times N\)의 matrix
    • row index : k
    • column index : \(n\)
    • \(W_{kn}\) : \(e^{\frac{-i 2\pi k n}{N}}\)
  • 여기서 \(W\)를 DFT matrix라고 한다

.

\(W=\frac{1}{\sqrt{N}}\left[\begin{array}{cccccc} 1 & 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^{2} & \omega^{3} & \cdots & \omega^{N-1} \\ 1 & \omega^{2} & \omega^{4} & \omega^{6} & \cdots & \omega^{2(N-1)} \\ 1 & \omega^{3} & \omega^{6} & \omega^{9} & \cdots & \omega^{3(N-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{N-1} & \omega^{2(N-1)} & \omega^{3(N-1)} & \cdots & \omega^{(N-1)(N-1)} \end{array}\right]\).

where \(\omega=\exp (-2 \pi i / N)\)

5. Fast Fourier Transform (FFT) with numpy

FFT (Fast Fourier Transform) refers to a way the discrete Fourier Transform (DFT) can be calculated efficiently (numpy)

• 직접 구현한 discrete_fourier_transform

import matplotlib.pyplot as plt

X_time=np.sin(np.arange(256))

def discrete_fourier_transform(X):
    N = len(X)
    n = np.arange(0,N)
    k = n.reshape(N,1)
    W = np.exp(-2j * np.pi * k * n / N)
    return np.dot(W,X)    

• numpy에서 제공하는 np.fft.fft
  • X_freq1.real : 실수 부분
  • X_freq1.imag : 허수 부분

X_freq1 = discrete_fourier_transform(X_time)
X_freq2 = np.fft.fft(X_time)

real_part=X_freq1.real
imag_part=X_freq1.imag

Reference

• https://ratsgo.github.io/speechbook/docs/fe/ft
• https://numpy.org/doc/stable/reference/generated/numpy.fft.fft.html#numpy.fft.fft
• https://www.youtube.com/watch?v=60cgbKX0fmE
• https://www.youtube.com/watch?v=wpHWGuof2nE