(paper) An Unsupervised Neural Attention Model for Aspect Extraction

An Unsupervised Neural Attention Model for Aspect Extraction (2017)

Contents

1. Abstract

2. Introduction
3. Model Description
   1. Sentence Embedding with Attention
   2. Sentence Reconstruction with Aspect Embeddings
   3. Training Objective
   4. Regularization Term

0. Abstract

“Neural” approach for “Aspect Extraction (AE)”

• distribution of word co-occurences, via “embedding”
• “attention” to de-emphasize irrelevant words

1. Introduction

example)

• [ sentence ] “The beef was tender and melted in my mouth”
• [ aspect term ] “beef”

2 subtasks in AE

• 1) extract all aspect terms
  • ex) “beef”
• 2) cluster aspect terms
  • ex) “beef”, “chicken”, “hamburger” \(\rightarrow\) “food”

Previous works

• 1) rule-based

• 2) supervised

• 3) unsupervised

  • ex) LDA : models the ..

    • corpus as “mixture of topics(aspects)”
    • topics as “distribution over word types”

  • problems of LDA :

    • do not directly encode word co-occurrence statistics

    • only implicitly capture such patterns, by modeling word generation from ‘document level’

      ( assumption : word is generated “INDEPENDENTLY” )

    • BUT…..review documents tend to be short!

ABAE (Attention-based Aspect Extraction)

• tackle the problem of LDA
• Two key points
  • 1) embedding ( co-occur \(\rightarrow\) close embedding space )
  • 2) attention ( filter (un)important words )

2. Model Description

(1) goal : learn a set of “aspect embeddings”

(2) notation :

• feature vector \(\mathbf{e}_{w} \in \mathbb{R}^{d}\)
• word embedding matrix : \(\mathbf{E} \in \mathbb{R}^{V \times d}\)
• aspect embedding matrix : \(\mathbf{T} \in \mathbb{R}^{K \times d}\)
• size
  • \(V\) : vocabulary size
  • \(d\) : latent dimension
  • \(K\) : number of aspects ( « \(V\) )

(3) input : list of indexes for words ( in a review sentence )

(4) Flow

• 1) dimension reduction
• 2) reconstruction

(5) Process ( in detail )

• step 1) filter away non-aspect words
  • by “down weighting”, via “attention”
• step 2) construct sentence embedding \(\mathbf{z}_{s}\)
  • from “weighted” word embeddings
• step 3) reconstruct sentence embedding \(\mathbf{r}_{s}\)
  • linear combination of aspect embeddings ( from \(\mathbf{T}\) )

( Summary )

• transform sentence embeddings of filtered sentences \(\mathbf{z}_{s}\)
• into their reconstruction \(\mathbf{r}_{s}\)
• with the least possible amount of distortion
• preserve most of the info of aspect words in \(K\) embedded aspects

3.1 Sentence Embedding with Attention

Construct \(\mathbf{z}_{s}\) ( sentence embedding )

• want to capture most relevent info w.r.t “ASPECT” of sentence

• \(\mathbf{z}_{s}\) = weighted sum of word embeddings \(\mathbf{e}_{w_{i}}, i=1, \ldots, n\)

• \(\mathbf{z}_{s}=\sum_{i=1}^{n} a_{i} \mathbf{e}_{w_{i}}\).

  • \(a_{i}\) : attention weight

    ( probability that \(w_i\) is the appropriate word to focus on (to capture main topic) )

    • \(a_{i} =\frac{\exp \left(d_{i}\right)}{\sum_{j=1}^{n} \exp \left(d_{j}\right)}\).
    • \(d_{i} =\mathbf{e}_{w_{i}}^{\top} \cdot \mathbf{M} \cdot \mathbf{y}_{s}\).
      • \(\mathbf{M} \in \mathbb{R}^{d \times d}\) : mapping between “global context embedding \(\mathbf{y_s}\)” & “word embedding \(\mathbf{e}_{w}\)”
    • \(\mathbf{y}_{s} =\frac{1}{n} \sum_{i=1}^{n} \mathbf{e}_{w_{i}}\). ( = average of word embeddings )

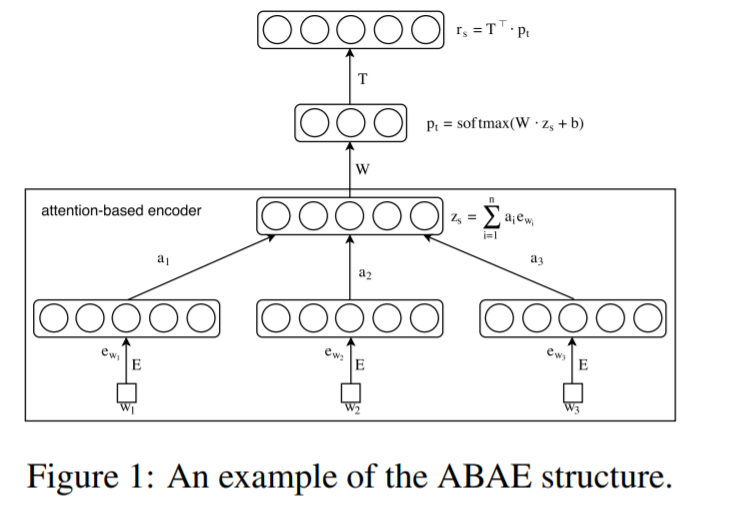
3-2. Sentence Reconstruction with Aspect Embedding

• Similar to Autoencoder

• Reconstruction = linear combination of aspect embeddings from \(\mathbf{T}\)

\(\mathbf{r}_{s}=\mathbf{T}^{\top} \cdot \mathbf{p}_{t}\).

• \(\mathbf{r}_{s}\) :
  • reconstructed vector representation
• \(\mathbf{p}_{t}\) :
  • weight vector over \(K\) aspect
  • obtained by reducing \(\mathbf{z}_{s}\) from \(d\) to \(K\)
  • \(\mathbf{p}_{t}=\operatorname{softmax}\left(\mathbf{W} \cdot \mathbf{z}_{s}+\mathbf{b}\right)\).
• \(\mathbf{T}\) :
  • aspect embedding matrix

3-3. Training Objective

minimize “RECONSTRUCTION error”

• ( max-margin objective function )

Negative Sampling

• randomly sample \(M\) sentences

Goal : make the “reconstructed embedding \(\mathbf{r}_s\)”

• similar to the “target sentence embedding \(\mathbf{z_s}\)“

• different from “negative samples”

\(J(\theta)=\sum_{s \in D} \sum_{i=1}^{m} \max \left(0,1-\mathbf{r}_{s} \mathbf{z}_{s}+\mathbf{r}_{s} \mathbf{n}_{i}\right)\).

3-4. Regularization Term

Aspect embedding matrix \(\mathbf{T}\) :

• may suffer from “redundancy problem”

To ensure DIVERSITY, add regularization term

• \(U(\theta)=\left\|\mathbf{T}_{n} \cdot \mathbf{T}_{n}^{\top}-\mathbf{I}\right\|\).

Final Objective

• \(L(\theta)=J(\theta)+\lambda U(\theta)\).