DOER : Dual Cross-Shared RNN for Aspect Term-Polarity Co-Extraction (2019)
Contents
0. Abstract
ABSA의 2가지 task
- 1) aspect term extraction (ATE)
- 2) aspect sentiment classification (ASC)
이 둘을 같이 하는 aspect term-polarity co-extraction
이 논문은 위의 2개의 task를 two sequence labeling problems로 취급
propose DOER (Dual crOss-sharEd RNN framework)
1. Introduction
ATE & ASC를 simultaneously 수행!
하지만, 이 둘은 동시에 하기가 쉽지 않았다! 여러 문제들로 인해..
-
문제 1) ATE and ASC are quite different tasks
- ATE : sequence labeling task
- ASC : classification task
따라서, 주로 pipeline 방식으로 두개를 순차적으로 풀어나갔었음
\(\rightarrow\) 해결책 : ASC를 “sequence labeling task”으로 풀기
-
문제 2) The number of aspect term-polarity pairs in a sentence is arbitrary
- 일부 문장은 2개의 term-polarity pair
- 일부 문장은 1개의 ~

-
1) pipelined approach
-
step 1 : label the given sentence using aspect term tags (B/I/O)
-
step 2) : feed aspect terms into classifier to get polarities
-
-
2) collapsed approach
- B-PO/ I-PO 등의 tag 사용
-
3) joint approach
-
jointly labels each sentence with 2 different tags
( aspect term tags & polarity tags )
-
collapsed approach 보다 더 feasible
( \(\because\) combined tags of collapsed approach make the learned representation confused )
-
DOER (Dual crOss-sharEd RNN framework)
-
end to end 방식
- generate all aspect term-polarity pairs
- dual RNN & cross-shared unit (CSU) 사용
- CSU : ATE와 ASC사이의 interaction을 캐치하고자 만들어짐
- 2개의 auxiliary task
- 1) aspect length enhancement
- 2) sentiment enhancement
- propose Residual Gated Unit (ReGU)
Contributions
- 1) DOER를 제안함 ( end-to-end 방식 + CSU 제안됨 )
- 2) 2개의 auxiliary task를 제안함 ( + ReGU 통한 feature extraction 성능 \(\uparrow\) )
2. Methodology
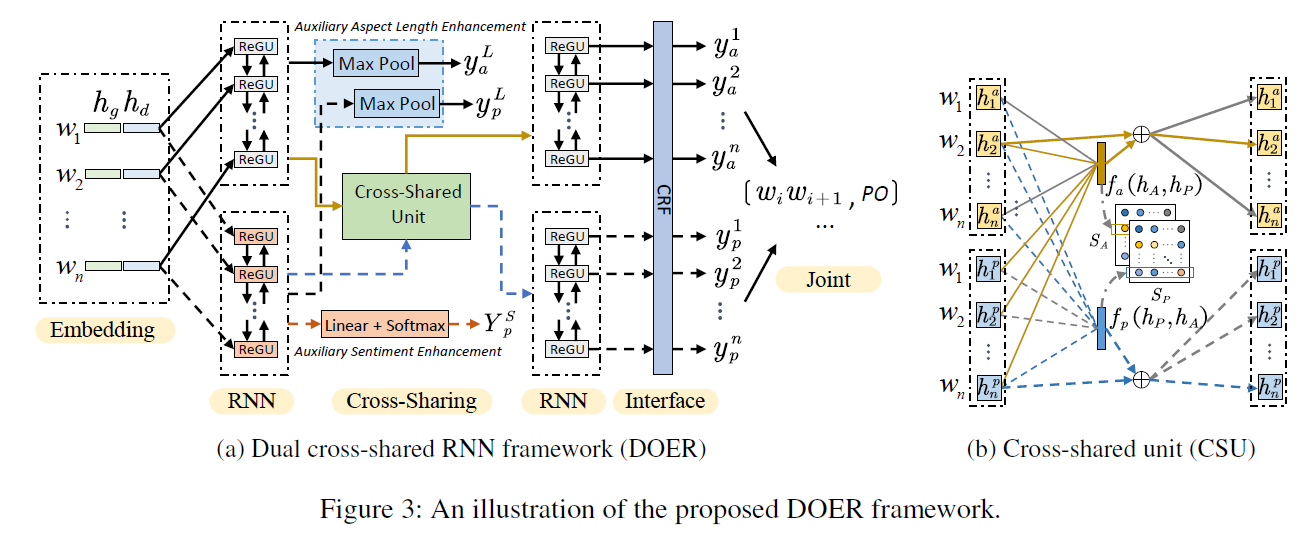
2-1) Problem Statement
- aspect term-polarity co-extraction을 풀고자
- 2개의 sequence labeling task로 취급
Notation
-
\(S=\left\{w_{i} \mid i=1, \ldots, n\right\} .\).
-
ATE의 목적 : 각 단어 \(w_i\)에 대해 tag을 assign 하기 \(t_{i}^{a} \in T^{a}\)
-
ASC의 목적 : \(\sim\) \(t_{i}^{p} \in T^{p}\)
( \(T^{a}=\{\mathrm{B}, \mathrm{I}, \mathrm{O}\}\) and \(T^{p}=\{\mathrm{PO}, \mathrm{NT}\}\) )
-
2-2) Model Overview
Word Embedding
- double embeddings 사용
- 1) general-purpose embeddings : \(\mathrm{G} \in \mathbb{R}^{d_{G} \times \mid V \mid }\)
- 2) domain-specific embeddings : \(\mathrm{D} \in \mathbb{R}^{d_{D} \times \mid V \mid }\)
- each word \(w_i\) will be initialized with a feature vector \(h_{w_{i}} \in \mathbb{R}^{d_{G}+d_{D}}\)
- \(h_{w_{i}}=G\left(w_{i}\right) \oplus D\left(w_{i}\right)\) ( concatenation )
Stacked Dual RNNs
- main architecture of DOER : “stacked dual RNNs”
- 1) for ATE
- 2) for ASC
- RNNs의 layers들은 bidirectional ReGU
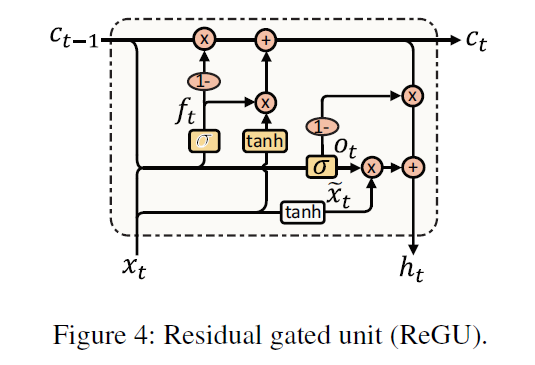
Cross-Shared Unit (CSU)
-
BiReGU이후, representation을 생성함
( = info of ATE & info of ASC …. 각각은 현재 separated 되어있음 )
-
하지만, 현실은 이 두 label은 strong relation
\(\rightarrow\) 이를 캐치하기 위해 CSU사용
-
그러기 위해, composition vector (\(\alpha_{i j}^{M} \in \mathbb{R}^{K}\)) 만든다
\(\alpha_{i j}^{M}=f_{m}\left(h_{i}^{m}, h_{j}^{\bar{m}}\right)=\tanh \left(\left(h_{i}^{m}\right)^{\top} G^{m} h_{j}^{\bar{m}}\right)\).
- \[M \in\{A, P\}, m \in\{a, p\}, h_{i}^{m} \in h_{M}\]
- \[G^{m} \in\mathbb{R}^{K \times 2 d \times 2 d}\]
-
위에서 만든 composition vector로 attention score 계산
\(S_{i j}^{M}=v_{m}^{\top} \alpha_{i j}^{M}\). ( scalar 이다 )
\(\rightarrow\) 이를 모아서 두 개의 matrices \(S_A, S_P\)를 만든다
-
higher score \(S_{ij}^A\) = aspect term \(i\)와 polarity representation \(j\)-th word의 correlation \(\uparrow\)
-
enhance the original ATE / ASC features
\(h_{M}=h_{M}+\operatorname{softmax}_{r}\left(S^{M}\right) h_{\bar{M}}\).
Interface
- to generate final ATE & ASC tags…
- 방법 1) dense layer + softmax
- 방법 2) CRF
- 방법 1) 보다 high dependency between tags를 포착할 수 있어
- \(L\left(W_{c}, b_{c}\right)=\sum_{i} \log p\left(y \mid h ; W_{c}, b_{c}\right)\).
Joint Input
After generating the labels for ATE & ASC..
마지막 step : obtain the aspect term-polarity pairs
aspect term을 polarity label의 boundary로써 생각을 하고,
count the number of each polarity category!
( maximum number의 것으로 채택 ( 만약 동일하면 first label 것으로 ) )
- ex) PO NT -> PO
- ex) PO PO -> PO
- ex) PO NT NT -> NT
Auxiliary Aspect Term Length Enhancement
(Auxiliary Task 1) predict the average length of aspect terms
- \(z_{u_{A}}=\sigma\left(W_{u_{A}}^{\top} \tilde{h}_{A}\right)\).
- loss : \(\mathcal{L}_{u_{A}}=\mid \mid z_{u_{A}}-\hat{z}_{u} \mid \mid ^{2}\)
- \(\hat{z}_{u}\) : average length of aspect terms
Auxiliary Sentiment Lexicon Enhancement
(Auxiliary Task 2) use sentiment lexicon to guide ASC
-
이 lexicon을 사용하여, 각 word를 sentiment label로 mapping
-
\(z_{i}^{s}=\operatorname{softmax}\left(W_{s}^{\top} h_{i}^{p, l_{1}}\right)\).
-
where \(W_{s} \in \mathbb{R}^{2 d \times c}\) is a weight parameter,
( \(c=3\) means the set {positive, negative, none \(\}\) )
-
-
loss : \(\mathcal{L}_{s}=-\frac{1}{n} \sum_{i=1}^{n}\left(\mathbb{I}\left(\hat{y}_{i}^{S}\right)\left(\log \left(z_{i}^{s}\right)\right)^{\top}\right)\).
2-3) Joint Loss
-
꼴 : \(L\left(W_{c}, b_{c}\right)=\sum_{i} \log p\left(y \mid h ; W_{c}, b_{c}\right)\)
-
Joint Loss :
\(\mathcal{J}(\Theta)=\left(\mathcal{L}_{a}+\mathcal{L}_{p}\right)+\left(\mathcal{L}_{u_{A}}+\mathcal{L}_{u_{P}}+\mathcal{L}_{s}\right)+\frac{\lambda}{2} \mid \mid \Theta \mid \mid ^{2}\).
