Seunghan Lee

Seunghan Lee

Deep Learning, Data Science, Statistics

Toward Tag-free ABSA ; A Multiple Attention Network Approach (2020)

Contents

  1. Abstract
  2. Introduction
  3. Model Description
    1. Notation & Problem Formulation
    2. Model Architecture
    3. Loss Function
    4. Aspect Ranking Scheme


0. Abstract

대부분의 요즈음 ABSA task의 문제점

  • 1) heavily rely on manual tagging
  • 2) aspect 별 감정이, overall 감정에 HOW/WHY 영향을 미쳤는지 설명 X


이를 극복하기 위한 알고리즘 “MAN (Multiple Attention Network)”를 제안함

  • 특징 1) aspect tag 필요 없음
  • 특징 2) aspect & overall 감정 둘 다 포착 O
  • 특징 3) overall 감정에 중요한(vital) 역할을 한 aspect 포착 O
    • “aspect ranking scheme”을 사용함으로써!
  • (기타) Trip Advisor에서 크롤링한 데이터를 사용함


1. Introduction

Abstract에서 말한 기존 ABSA 알고리즘들의 문제점을 극복하기 위해, MAN approach를 제안함

  • TAG-FREE review를 directly 사용함

    ( “aspect level” & “overall” ratings 은 주어져 있음 )

    ( ex. 분위기5점, 맛3점 등… & 종합 점수 4점 )

  • 두 종류의 Attention 사용

    • (1) Self-attention
    • (2) Position-Aware attention

  • 각 단어/절이 aspect-level &overall 감정에 얼마나 영향을 미쳤는지(=weighted contribution) 파악 가능

  • overall 감정에 영향 미친 중요한 (vital) aspect 포착 가능


Contribution 요약

  • 1) data sparsity 문제를 해결함 ( = 문장 어느 단어가 어떤 속성인지 manual tagging이 없는 상황 )
  • 2) Explainable하다 ( = overall 감정에 어떠한 aspect이 얼마나 영향 미쳤는지 알 수 O )
  • 3) 직접 크롤링한 Trip Advisor데이터를 사용함


2. Model Description

2-1. Notation & Problem Formulation

Notation

  • n개의 review들 : \(\boldsymbol{R}=\left\{r_{1}, r_{2}, \ldots, r_{n}\right\}\)

  • review별 단어들 ( 하나의 review에 \(m\)개 단어 ) : \(r=\left(\mathrm{w}_{1}, \mathrm{w}_{2}, \ldots, \mathrm{w}_{j}, \ldots, \mathrm{w}_{m}\right)\)

  • 두 종류의 ratings

    ( ratings과 polarity 혼동 주의! )

    • 1) overall ratings ( 1~5 )
      • overall polarity : \(P^{o}\)
    • 2) aspect ratings ( 1~5 )
      • aspect polarity : \(P^{k}\) , where \(k \in \{1, \ldots, K\}\) ( 총 \(K\)개의 aspect 종류들 )

Goal : \(P^{k}\) 와 \(P^{o}\) 찾기

  • \(P^{k}\)들을 사용하여 \(P^{o}\)를 찾기!
  • (혹시나) 뒤에서 나오는 notation과 유의!
    • \(y^k\)는 predicted sentiment polarity “PROBABILITY DISTRIBUTION”
    • \(P^k\) 는 predicted sentiment polarity “CLASS”


2-2. Model Architecture

4개의 module로 구성됨

( 각 module에 세부 정보는 뒤에 이어서! )

  • 1) Embedding

    • 요약 ) (a) review sentence & (2) 각 단어의 position을 임베딩하여
    • low-level semantic을 잡아냄

  • 2) Hidden States

    • 요약 ) 위의 EMBED(a) & EMBED(b)를 input으로 받은 뒤
    • high-level semantic을 잡아냄

  • 3) Attention Encoder

    • 요약 ) multiple-attention을 사용하여
    • \(P^{k}\)에 중요한 영향을 미치는 “vital 단어”를 잡아낸다

  • 4) Sentiment Classifier

    • 요약 ) 위의 2개의 attention의 결과를 concatenate (=final representation)한 뒤,
    • FC layer 태워서 최종적인 \(P^{o}\)를 계산한다

  • 위의 4개의 모듈을 거친 뒤, Model-agnostic aspect ranking scheme을 사용하여,

    \(P^{o}\)에 중요한 영향을 미치는 “vital aspect”를 잡아낸다


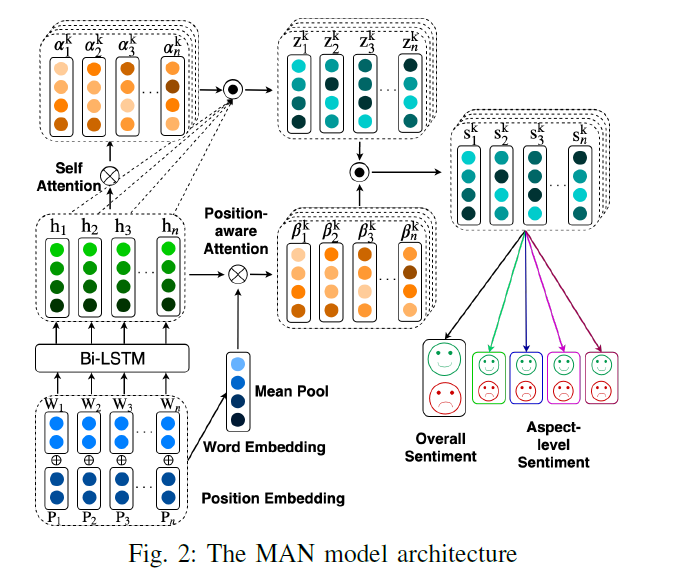
figure2


[module 1] Embedding

두 가지를 임베딩한다

  • 1) review sentence의 각 단어들
    • with GloVe
    • 차원 : \(w_{j} \in \mathbb{R}^{ \mid V \mid }\) \(\rightarrow\) \(e_{j} \in \mathbb{R}^{d \times 1}\)
  • 2) 각 단어들의 position
    • “absolute” position을 임베딩한다
    • 마찬가지로 \(\mathbb{R}^{d \times 1}\) 차원으로 임베딩

그런 뒤, 위의 2가지 embedding 결과를 합친다! ( 차원 : \(\boldsymbol{E} \in \mathbb{R}^{2 d \times V}\) )

이를 통해 lower-level semantic을 잡아낸다


[module 2] Hidden States

  • LSTM & biLSTM 모두 사용 가능
  • 이를 통해 higher-level semantic을 잡아낸다
  • \(\boldsymbol{H}=\operatorname{LSTM}(E)=\left(h_{1}, h_{2}, \ldots, h_{i}, \ldots, h_{n}\right)\).
    • \(n\) = hidden state의 개수 ( 앞서 말한 리뷰 개수 \(n\) 아님! notation 딴 것좀 써주지… )


[module 3] Attention Encoder

각 aspect-level 감정에 영향을 미치는 중요한 information을 잡아낸다

2가지 attention으로 구성

  • 1) Self Attention
    • 역할 : aspect-level 감정에 영향 미치는 중요한 word 포착 ( =filter context words)
  • 2) Position-Aware Attention
    • 역할 : 위에서 filtering된 word들 사이의 relevance 포착


(수식) Self Attention ( \(z_{i}\) 구하기 )

\(z_{i}=\sum_{i=1}^{n} \alpha_{i} h_{i}\).

  • \(\alpha_{i}=\frac{\exp f_{i}}{\sum_{j=1}^{n} \exp f_{j}}\).
    • \(f_{i}=\tanh \left(h_{i} \boldsymbol{W}_{\alpha} \boldsymbol{h}_{\boldsymbol{i}}^{T}+b_{\alpha}\right)\).


이렇게 구한 \(z_i\)를, Position-Aware Attention으로 넘긴다.


(수식) Position-Aware Attention ( \(s_{i}\) 구하기 )

\(s_{i}=\sum_{i=1}^{n} \beta_{i} \boldsymbol{z}_{\boldsymbol{i}}\).

  • \(\beta_{i}=\frac{\exp g_{i}}{\sum_{j=1}^{n} \exp g_{j}}\).

    • \(\boldsymbol{g}_{\boldsymbol{i}}=\tanh \left(\overline{\boldsymbol{h}} \boldsymbol{W}_{\beta} \boldsymbol{h}_{\boldsymbol{i}}^{T}+b_{\beta}\right)\).

      ( 여기서 \(\bar{h}\) 는 AVERAGE(word & position embedding) )


[module 4] Sentiment Classifier

요약

  • aspect level & overall 감정을 포착하기 위해!

  • 위의 [module 3] Attention Encoder에서 최종적으로 구해진 \(s_{k}\) 를 사용!
  • final overall representation : \(s^{o}=\left[s^{1} ; s^{2} ; \ldots ; s^{k}\right]\)

최종 예측 결과

  • \(C=2\)를 가정함 ( 긍정 & 부정 ) … ( \(y^{k},y^{o} \in \mathbb{R}^{C}\) )
  • aspect 별 감정 예측 결과 : \(y^{k} =\operatorname{softmax}\left(\boldsymbol{W}_{k} \boldsymbol{s}^{k}+b_{k}\right)\).
  • overall 감정 예측 결과 : \(y^{o} =\operatorname{softmax}\left(\boldsymbol{W}_{o} \boldsymbol{s}^{o}+b_{o}\right)\)


[기타] Regularization Term

Orthogonal Regularization을 사용함

\(\begin{aligned} \boldsymbol{M}_{\alpha} &=\left[\boldsymbol{\alpha}^{1} ; \boldsymbol{\alpha}^{2} ; \ldots ; \boldsymbol{\alpha}^{k}\right] \\ \boldsymbol{M}_{\beta} &=\left[\boldsymbol{\beta}^{1} ; \boldsymbol{\beta}^{2} ; \ldots ; \boldsymbol{\beta}^{k}\right] \\ \mathcal{R}_{\alpha} &= \mid \mid \boldsymbol{M}_{\alpha}^{\mathrm{T}} \boldsymbol{M}_{\alpha}-\boldsymbol{I} \mid \mid _{2} \\ \mathcal{R}_{\beta} &= \mid \mid \boldsymbol{M}_{\beta}^{\mathrm{T}} \boldsymbol{M}_{\beta}-\boldsymbol{I} \mid \mid _{2} \end{aligned}\).


2-3. Loss Function

  • end-to-end 방식

  • Cross-entropy loss 사용

  • loss_function ( target sentiment polarity, predicted sentiment polarity )

  • \(\begin{aligned} &\mathcal{L}_{k}=-\hat{y}^{k} \log \left(y^{k}\right)-\left(1-\hat{y}^{k}\right) \log \left(1-y^{k}\right), \\ &\mathcal{L}_{o}=-\hat{y}^{o} \log \left(y^{o}\right)-\left(1-\hat{y}^{o}\right) \log \left(1-y^{o}\right), \end{aligned}\).

    • \(\hat{y}^{k}\) & \(\hat{y}^{o}\) : 각각 aspect-level & overall target sentiment polarity ( TRUE 값 )

    • 왜 true 값에 hat을 씌우는지 참..

  • 최종 Loss Function

    • 1) Cross-entropy loss
    • 2) Orthogonal Regularization
    • 3) L2 Regularzation

    \(\mathcal{L}=\mathcal{L}_{o}+\lambda_{1} \sum_{k=1}^{\delta} \mathcal{L}_{k}+\lambda_{2} \mathcal{R}_{\alpha}+\lambda_{3} \mathcal{R}_{\beta}+\lambda_{4} \mid \mid \boldsymbol{\theta} \mid \mid ^{2},\).

    • \(\delta\) : (hyper-parameter) number of aspects underlined in review texts
    • \(\lambda_{1}, \lambda_{2}, \lambda_{3}\), and \(\lambda_{4}\) : tuning parameters to leverage RELATIVE IMPORTANCE


2-4. Aspect Ranking Scheme

두 가지 attention weight값들을 사용함

  • (1) self-attention weight : \(\alpha_i\)
  • (2) Position-aware attention weight : \(\beta_i\)

최종적인 Score :

  • \(\text { score }^{k}=\sum_{j=1}^{m}\left(\alpha_{j}^{k}+\beta_{j}^{k}\right)\).
    • \(\alpha_i^k\) : \(k^{th}\) aspect을 나타내는 \(i\)번째 단어 ( in Self-attention )
    • \(\beta_i^k\) : \(k^{th}\) aspect을 나타내는 \(i\)번째 단어 ( in Position-aware attention )
  • \(\text { score }^{k}\) 의 의미 : summarized importance score of \(k^{th}\) aspect


You May Also Enjoy

3 minute read

6 minute read

4 minute read

less than 1 minute read