(paper) Target-specified Sequence Labeling with Multi-head Self-attention for Target-oriented Opinion Words Extraction (2021)

Target-specified Sequence Labeling with Multi-head Self-attention for Target-oriented Opinion Words Extraction (2021)

Contents

1. Abstract
2. Introduction
3. Related Work
   1. TOWE
   2. AOPE
4. Methodology
   1. Task Description
   2. Framework
   3. Multi-head Self-Attention
   4. Target-Specified Encoder
   5. Decoder & Training

0. Abstract

ABSA의 main task 2개

• Opinion target Extraction
• Opinion term extraction

최근의 ABSA 연구들은 TOWE!

TOWE (Target-oriented Opinion Words(Terms) Extraction )

• opinion target(=aspect)가 주어졌을 때, opinion word 맞추기

• ex) Input : 문장 & “음식의 맛” — output : 달달하다

• 이를 추가로 AOPE로 확장 가능

AOPE (Aspect-Opinion Pair Extraction)

• extract aspect(=opinion target) & opinion terms IN PAIRS
• TOWE vs AOPE
  • TOWE : aspect가 주어졌을 때, opinion word(term) 찾기
  • AOPE : aspect와 opinion word(term) 을 쌍으로 찾기

이 논문은 아래의 (1) & (2)를 제안한다

• (1) TOWE를 위한 “TSMSA”
• (2) AOPE를 위한 “MT-TSMSA”

1. Introduction

용어 정리

Aspect?

• 다른 표현 : opinion target

• word/phrase in review, referring to the object towards which users show attitudes

  ( ex. 음식의 맛, 공연의 가격대 )

Opinion terms

• words or phrases representing users’ attitudes

  ( ex. 맵다, 짜다, 비싸다 )

Example

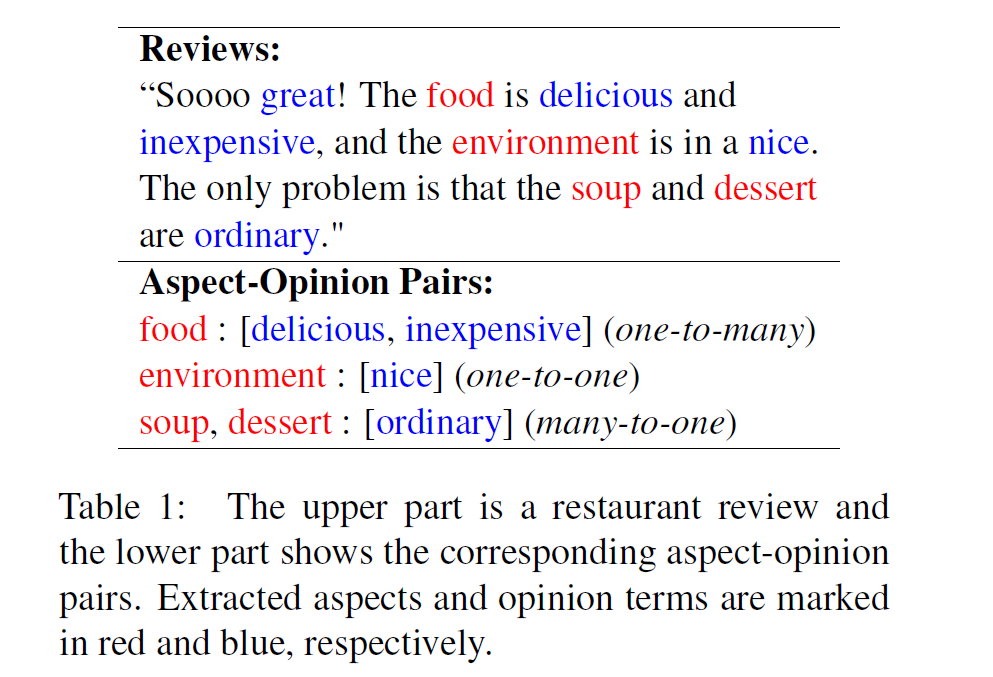
많은 방법론들의 문제점 :

​ ignore the relation of ASPECTS & OPINION TERMS

• 그래서 TOWE (Target-oriented Opinion Words Extraction) 가 필요한 것이다!

• 더 나아가서, AOPE (\(\approx\) PAOTE)가 나온 배경이기도!

  • AOPE = aspect and opinion term extraction + TOWE

    ( 그런데 aspect extraction은 이미 많이 연구되어서, 결국 핵심은 TOWE 이다! )

  • TOWE의 핵심 : ( 결국 AOPE의 핵심이 되겠지? )

    mine the relationship between ASPECTS & OPINION TERMS

    aspect & opinion term의 relationship은 복잡하다! (위의 그림 참조)

    ( one-to-one, one-to-many, many-to-one )

TSMSA ( + 기존의 TOWE 방법들의 문제점 )

• (기존 방법들) tuning해야할 hyperparameter들이 너무 많다!

• 이 논문에서 제안하는 (TOWE 기반) 방법인 TSMSA는 이를 극복한다!

  • capable of capturing the information of the specific aspect

  • [SEP] aspect [SEP]으로 우선 전처리된다.

    ex) “The [SEP] food [SEP] is delicious”

MT-TSMSA

• AOPE = aspect and opinion term extraction + TOWE
• MT-TSMSA는 AOPE 기반 방법

Contribution

• 1) propose a target-specified sequence labeling method with multi-head self attention to perform TOWE
• 2) TSMSA & MT-TSMSA를 위해, very little hyperparemter to tune

2. Related Works

2-1) TOWE

다양한 방법론

• 1) aspect extraction
• 2) opinion term extraction
• 3) 둘 다 동시에 ( co-extraction )

위 방법론들 모두 aspect & opinion term사이의 relationship을 무시한다

( Rule-based는 이를 고려한다 하더라도, 너무 expert knowledge에 depende해 )

TOWE ( Fan et al (2019) )

• extract opinion terms ( given aspect )
• use Inward-Outward LSTM
• 문제점 : BERT같이 파워풀한거 사용 X
• 이 논문은 BERT를 encoder로써 사용함으로서 성능 UP

2-2) AOPE

• extract aspects & opinion terms in PAIRS

• AOPE = aspect extraction + TOWE로 나눠서 볼 수 있다
• AOPE 관련 많은 방법들, hyperparameter 너무 많아

3. Methodology

3-1) Task Description

Notation

• sentence : \(s=\left\{w_{1}, w_{2}, \ldots, w_{n}\right\}\)

• 1) aspect ( = opinion target) : \(a=\left\{w_{i}, w_{i+1}, \ldots, w_{i+k}\right\}\)

• 2) opinion term : \(o=\left\{w_{j}, w_{j+1}, \ldots, w_{j+m}\right\}\)

  ( 둘 다 \(s\)의 substring이다 )

TOWE task : \(p(o \mid s, a)\)

AOPE task : \(p(<a,o> \mid s) = p(a \mid s) \times p(o \mid s,a)\)

3-2) Framework

TSMSA & MT-TSMSA의 structure는?

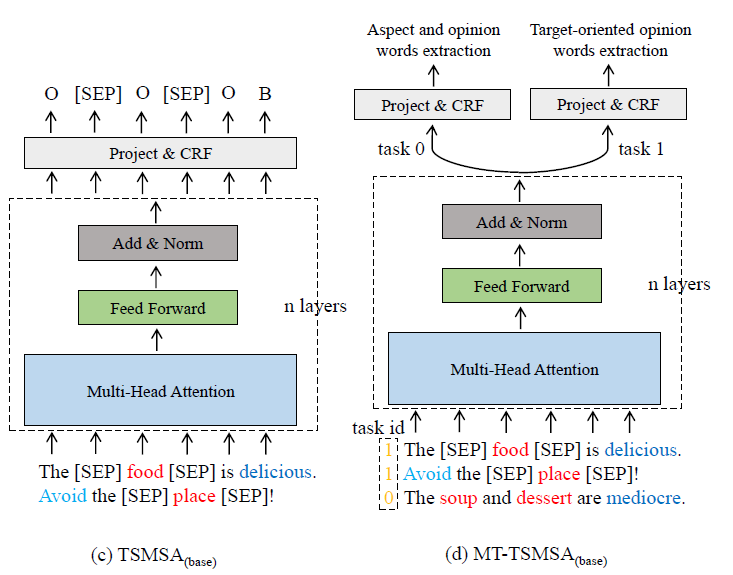
• step 1) aspect에 label을 붙이기 위해 “[SEP]” 을 양 옆에 사용한다
• step 2) Multi-head self attention 거쳐
• step 3) CRF 써서 sequence labeling 수행
• step 4) task 0 & task 1 are combined for multi-task learning

3-3) Multi-head Self-Attention

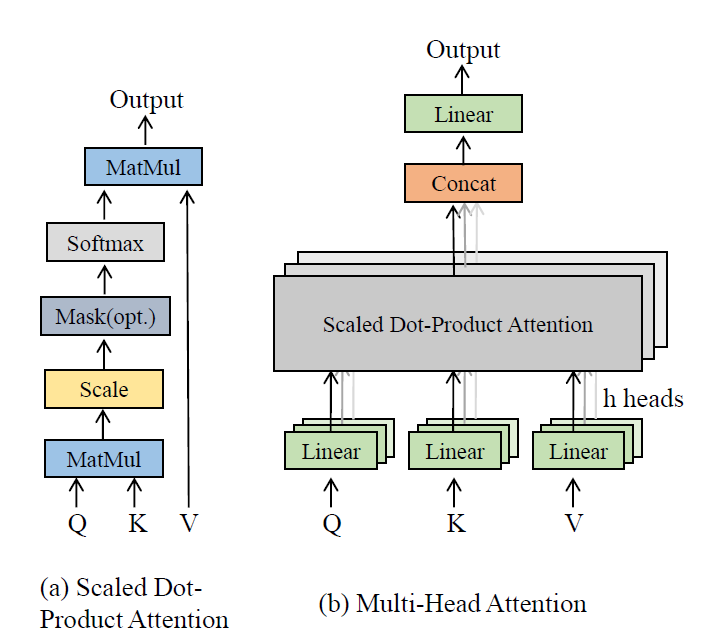
3-4) Target-Specified Encoder

• BERT 사용

3-5) Decoder & Training

• sequential representation \(H^{l}\)
• sequential label \(Y=\left\{y_{1}, \ldots, y_{n}\right\}\)
  • \(y_{i} \in\{\mathrm{B}, \mathrm{I}, \mathrm{O},[\mathrm{SEP}]\}\). or
  • \(y_{i} \in\{\mathrm{B}-\mathrm{ASP}, \mathrm{I}-\mathrm{ASP}, \mathrm{B}-\mathrm{OP}, \mathrm{I}-\mathrm{OP}, \mathrm{O}\}\).
• 위 둘을 사용하여, compute \(p\left(Y \mid H^{l}\right)\)

Single Task version

• 수식 생략 ( 그림 참조 )
• predicted output : \(p\left(Y \mid H^{l}\right)=\frac{\exp \left(S\left(H^{l}, Y\right)\right)}{\sum_{\tilde{Y} \in Y_{a l l}} \exp \left(S\left(H^{l}, \tilde{Y}\right)\right)}\).
• loss function : \(L(s)=-\log p\left(Y \mid H^{l}\right)\).

Multi Task version

• predicted output :

  • \(p\left(Y^{0} \mid H^{l}, i d=0\right)=\frac{\exp \left(S_{0}\left(H^{l}, Y^{0}\right)\right)}{\sum_{\tilde{Y} \in Y_{a l l}^{0}} \exp \left(S_{0}\left(H^{l}, \tilde{Y}\right)\right)}\).
  • \(p\left(Y^{1} \mid H^{l}, i d=1\right)=\frac{\exp \left(S_{1}\left(H^{l}, Y^{1}\right)\right)}{\sum_{\tilde{Y} \in Y_{a l l}^{1}} \exp \left(S_{1}\left(H^{l}, \tilde{Y}\right)\right)}\).

• loss function :

  • \(L(s, i d)=-\log p\left(Y \mid H^{l}, i d\right)\).

  • Given \(M\) sentences \(S=\left\{s_{1}, s_{2}, \ldots, s_{M}\right\}\) & \(i d=\left\{i d_{1}, \ldots, i d_{M}\right\}\), …

    \(J(\theta)=\sum_{k=1}^{M}\left(\left(1-i d_{k}\right) \lambda+i d_{k}\right) L\left(s_{k}, i d_{k}\right)\).