(paper) Aspect-Category based Sentiment Analysis with Hierarchical Graph Convolutional Network (2020)

Aspect-Category based Sentiment Analysis with Hierarchical Graph Convolutional Network (2020)

Contents

1. Abstract
2. Introduction
3. Problem Formalization
4. The Proposed Approach
   1. Feature Extraction with BERT
   2. Hier-GCN
      1. Category GCN Sub-Layer
      2. Category-Sentiment GCN Sub-Layer
   3. Hierarchical Prediction Integration

0. Abstract

대부분의 ABSA 연구들에서 말하는 “aspect”는..

• Explicit aspect (O)
• Implicit aspect (X)

둘 다 capture하기 위해, 이 논문은 Aspect-CATEGORY based sentiment analysis를 수행함

• (1) joint aspect category detection
• (2) category-oriented sentiment classification

ABSA task를 “category-sentiment hierarchy prediction”문제로써 바라본다.

• output : hierarchy output structure
  • (1) 리뷰 내의 multiple aspect categories를 identify
  • (2) 각각의 identified category에 대해 sentiment를 predict

Hier-GCN를 제안한다

• LOWER-level GCN : inner-relations among multiple categories
• HIGHER-level GCN : inter-relations between aspect categories & sentiments

1. Introduction

( 기존의 연구들 : ABSC, ATSA )

ABSC (Aspect Based Sentiment Classification )

• aspect 용어로부터 sentiment detect하기
• 한계점 : aspect 용어가 먼저 정해져야 (annotated)

ATSA (Aspect Term-based Sentiment Analysis )

• (1) aspect term extraction &
• (2) aspect sentiment classification을 jointly하게 수행
• 한계점 : only considers explicit aspects

이러한 위 두 방법론의 한계점에 대안으로, ACSA에 focus

ACSA (Aspect-Category based Sentiment Analysis)

• ATSA와 마찬가지로 (1) & (2)를 동시에 jointly하게 수행

• ATSA보다 나은 2가지?

  • (a) 리뷰 내에 명시적으로 해당 aspect term을 사용하지 않았어도 OK
  • (b) aspect term을 explicitly하게 뽑아내지 않아도, 문제 없음

  ( (a), (b) 다른게 뭐지…?? )

제안한 방법론 : Hier-GCN

• two-layer hierarchcy
  • lower : aspect 찾기 ( multi-label classification … 여러 aspect 존재 가능)
  • higher : sentiment 분류하기 ( multi-class classification … 하나의 sentiment만 가능 )
• 3개의 module로 구성
  • (1) BOTTOM module : 2개의 subtask을 위한 hidden representation을 얻기 위해 BERT 사용
  • (2) MIDDLE module : Hier-GCN
  • (3) TOP module : category-sentiment hierarchy prediction 수행

2. Problem Formalization

Notation :

• \(n\)개의 단어 : \(r=\left[w_{1}, \ldots, w_{n}\right]\)

• \(m\)개의 pre-defined aspect categories : \(\mathcal{C}=\left\{c_{1}, \ldots, c_{m}\right\}\)

• sentiment label들 : \(s=\) \(\{\) positive, negative, neutral }

ACSA의 Goal :

• category-sentence pair 생성하기 ( \(\left\{\ldots,\left(\hat{y}_{i}^{c}, \hat{y}_{i}^{s}\right), \ldots\right\}\) )
  • \(\hat{y}_{i}^{c}\) : \(i\) -th aspect category mentioned in \(r\)
  • \(\hat{y}_{i}^{s}\) : corresponding sentiment
• 위를 풀 수있는 여러 가지 대안/방안들?

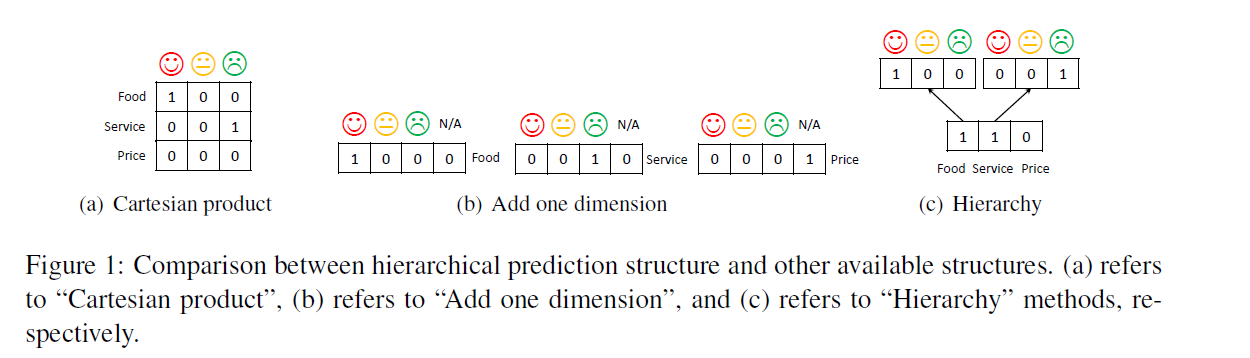
(1) Cartesian Product

• 모든 combination pair를 고려
• multi-label classification
• \(\hat{y}_{i}^{c}=0\) : \(c_i\) 카데고리의 부재
• 문제점 : 하나의 aspect에 대해 여러 sentiment 가능성 있음!

(2) Add one dimension

• 각 category에 대해, 감정 여부 1/0으로!

• multi-class classification

(3) Hierarchy

• 위의 (1) & (2)의 문제점 : two sub-task간의 internal relationship을 무시한다!

• ACSA task를 category-sentiment hierarchy prediction 문제로 취급한다

  \(p\left(\boldsymbol{y}^{c}, \boldsymbol{y}^{s} \mid \boldsymbol{r}\right)=p\left(\boldsymbol{y}^{c} \mid \boldsymbol{r}\right) p\left(\boldsymbol{y}^{s} \mid \boldsymbol{y}^{c}, \boldsymbol{r}\right),\).

  • \(p\left(\boldsymbol{y}^{c} \mid \boldsymbol{r}\right)\) : multi-label classification
  • \(p\left(\boldsymbol{y}^{s} \mid \boldsymbol{y}^{c}, \boldsymbol{r}\right)\) : multi-class classification

We adopt Bidirectional Encoder Representations from Transformers (BERT) as our sentence encoder, which is a pre-trained on a huge amount of text with masked language model and has been shown to achieve state-of-the-art results on a broad set of NLP tasks. Let \(H \in \mathbb{R}^{d \times(n+2)}\) denote the final hidden states generated from BERT, where we insert two special tokens (i.e., [CLS] and [SEP]) at the beginning and the end of each input \(r\). For space limitation, we omit a detailed description of BERT and refer readers to (Devlin et al., 2018).

For category representations, we further use \(m\) separate self-attention sub-layers on top of \(H\) to get the representations of \(m\) categories, denoted by \(C \in \mathbb{R}^{d \times m}\). Besides, following the practice in (Devlin

3. The Proposed Approach

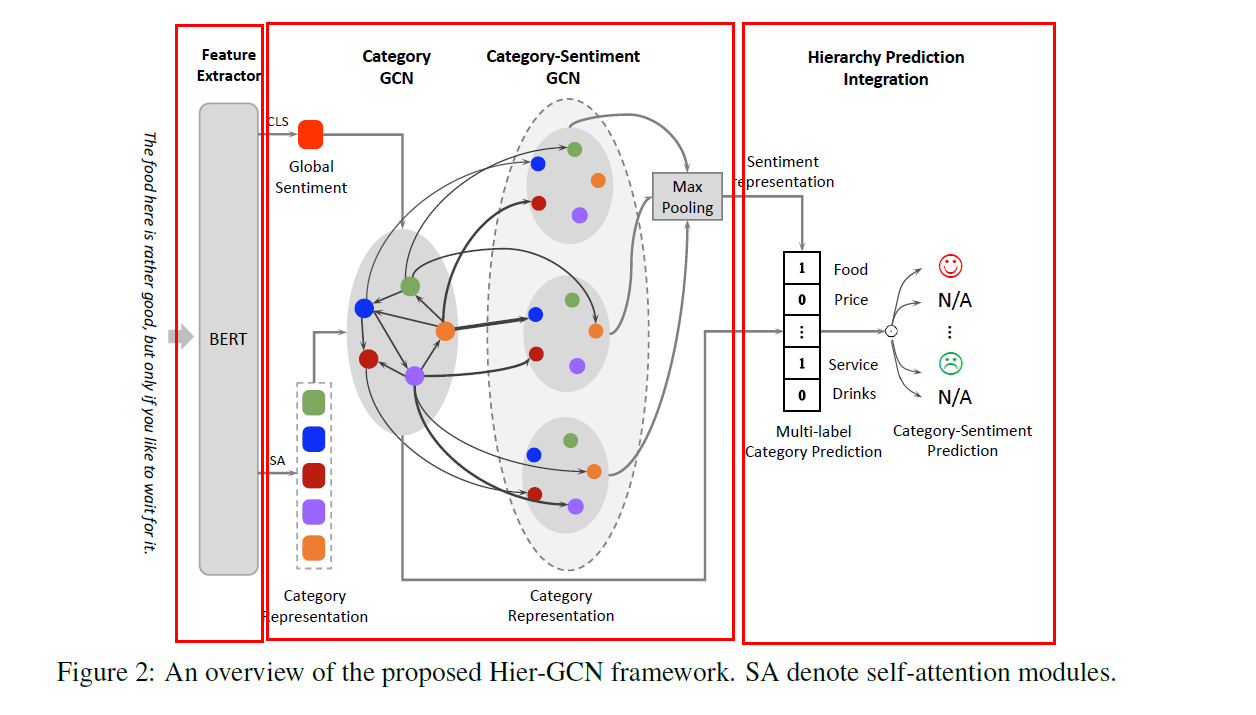
(1) BERT : basic encoder로 사용

(2) Hier-GCN : 아래의 2가지를 포착

• inner relation between multiple category
• inter relation between categories & sentiment polarities

(3) Hierarchical output & Integration module

3-1) Feature Extraction with BERT

• BERT사용해서 feature extraction

3-2) Hier-GCN

3-2-1) Category GCN Sub-Layer

• inner-relations ( between categories ) 잡아내기 위해
• directed graph ( 각 category = 각각의 node )
• obtain adjacent matrix \(M^{c} \in \mathbb{R}^{m \times m}\)
  • \(M_{i, j}^{c}\) 의 의미 : transition probability of having \(j\)th category, given \(i\)th category
  • \(M_{i, j}^{c}= \begin{cases}\frac{\operatorname{count}\left(c_{i}, c_{j}\right)}{\operatorname{count}\left(c_{i}\right)+1} & i \neq j, \\ 1 & i=j .\end{cases}\).
  • (서로 symmetric하지 않다)
• 위처럼 만들어진 matrix \(M^{c}\)로 graph convolution 수행
  • \(\boldsymbol{X}_{l+1}=f\left(\boldsymbol{W}_{l} \boldsymbol{X}_{l} \boldsymbol{M}^{c}+\boldsymbol{b}_{l}\right)\).
• 마지막 Hier-GCN layer에서, multi-label classification 수행해서 다양한 category를 찾아내!

3-2-2) Category-Sentiment GCN Sub-Layer

• inter-relations ( between categories & sentiment ) 잡아내기 위해

• directed graph ( \(m\)개의 category & \(3m\)개의 sentiment가 전부 node )

• \(M_{i, j}^{c-s}= \begin{cases}\frac{\operatorname{count}\left(c_{i},\left(s \mid c_{j}\right)\right)}{\operatorname{count}\left(c_{i}\right)+1} & i \neq j \\ 1 & i=j\end{cases}\).

  \(s \in\) \(\{\) positive, negative, neutral \(\} .\)

• sentiment-sensitive category representation

  \(\widehat{\boldsymbol{F}}_{l}=\operatorname{Tanh}\left(\boldsymbol{W}_{l}^{c, s} \boldsymbol{X}_{l+1} \oplus \boldsymbol{S}_{l}+\boldsymbol{b}_{l}^{c, s}\right)\).

  \(\widetilde{\boldsymbol{F}}_{l}^{s}=f\left(\boldsymbol{W}_{l}^{s} \widehat{\boldsymbol{F}}_{l} \boldsymbol{M}^{c-s}\right)\).

  \(\boldsymbol{S}_{l+1}=\operatorname{pooling}\left(\operatorname{dense}\left(\widetilde{\boldsymbol{F}}_{l}^{\text {pos }}\right) ; \operatorname{dense}\left(\widetilde{\boldsymbol{F}}_{l}^{\text {neg }}\right) ; \operatorname{dense}\left(\widetilde{\boldsymbol{F}}_{l}^{\text {neu }}\right)\right)\).

3-3) Hierarchical Prediction Integration

위에서 얻어낸..

• 3-1) category representation : \(\boldsymbol{X}_{i}\)
• 3-2) sentiment representation : \(S_{i}\)

을 사용하여, 다음을 계산한다.

\(\begin{gathered} p_{i}^{c}=p\left(y_{i}^{c} \mid \boldsymbol{r}\right)=\operatorname{sigmoid}\left(\boldsymbol{W}_{i}^{c} \boldsymbol{X}_{i}+b_{i}^{c}\right) \\ \boldsymbol{p}_{i}^{s}=p\left(\boldsymbol{y}_{i}^{s} \mid y_{i}^{c}, \boldsymbol{r}\right)=\operatorname{softmax}\left(\boldsymbol{W}^{s} \boldsymbol{S}_{i}+\boldsymbol{b}^{s}\right) \end{gathered}\).

이를 통해, 최종적으로..

• \(\left(\hat{y}_{i}^{c}, \hat{y}_{i}^{s}\right)=\left(\mathbb{I}\left(p_{i}^{c}>0.5\right), \arg \max \boldsymbol{p}_{i}^{s}\right)\).

ACSA의 loss part

• (1) multi-label classification ( CE loss )

  \(\operatorname{loss}^{c}=-\sum_{i=1}^{m} y_{i}^{c} \log p_{i}^{c}+\left(1-y_{i}^{c}\right) \log \left(1-p_{i}^{c}\right)\).

• (2) multi-class classification ( NLL )

  \(\operatorname{loss}^{s}=-\sum_{i=1}^{m} \sum_{j=1}^{3} \mathbb{I}\left(y_{i, j}^{s}\right) \log p_{i, j}^{s}\).

• 최종적인 loss : \(\operatorname{loss}=\operatorname{loss}^{c}+\operatorname{loss}^{s}\).