2.Markov Decision Process (MDP)

[ 2. Markov Decision Process (MDP) ]

1. Value function

어떤 행동이 좋은 행동인가? 이를 판단하기 위한 지표가 바로 VALUE FUNCTION

• 보상(reward) : Agent의 행동에 따라 받게 되는 것

• 할인율(discount factor, \(\gamma\)) : 미래의 받게되는 보상을 현재로 당겼을 때 할인하는 비율!

  • \(\gamma=0\) : 미래 고려 X
  • \(\gamma=1\) : 미래에 대한 고려가 커짐
• Return(G, total discount reward) :

  • 현재 시점에서, 미래에 받게되는 모든 reward까지 현재가치로 표현한 것.

  • \(G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... = \sum_{k=0}^{\infty }\gamma^k R_{t+k+1}\) .

    ( 여기서 $R_t$는 random variable이다 )

• 가치(Value, Value Function) :

  • 현재 상태에서, (앞으로) 기대되는 모든 return들의 합.
  • \(V(s) = E[R(s0)+ \gamma R(s1) + \gamma^2 R(s2) + .... \mid s0=s]\).

에이전트의 최종 목표 :

• “모든 상태에서 받는 Return값을 최대화하는 (=Value를 최대화하는) 최적의 정책 \(\pi^{\text{*}}\) 학습하기””

2. Bellman Equation

Value function은 크게 두 부분으로 나뉠 수 있다.

• 1) 지금 ( \(t\) 시점) 즉시 받는 보상값 ( \(R_{t+1}\) )
• 2) 미래 ( \(t+1\) 시점 ~ )에 받게되는 보상값들 ( \(\gamma\; v(S_{t+1})\) )

Bellman Equation 유도

\(\begin{aligned} v(s) &=\mathbb{E}\left[G_{t} \mid S_{t}=s]\right.\\ &=\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \mid S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma\left(R_{t+2}+\gamma R_{t+3}+\ldots\right) \mid S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma G_{t+1} \mid S_{t}=s\right] \\ &=\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) \mid S_{t}=s\right] \end{aligned}\).

Bellman Equation 풀기

\(v(s)=\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) \mid S_{t}=s\right]\). 식을 푸는 법?

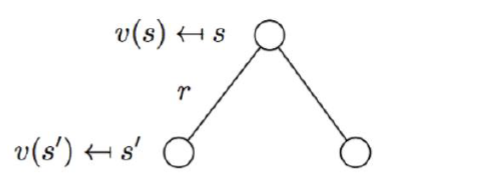
state-transition matrix가 있을 때 ( + state 수가 너무 많지 않을 때 ) :

• \(v(s)=\mathcal{R}_{s}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}} v\left(s^{\prime}\right)\).

• \(\left[\begin{array}{c} v\left(s_{1}\right) \\ \vdots \\ v\left(s_{N}\right) \end{array}\right]=\left[\begin{array}{c} r\left(s_{1}\right) \\ \vdots \\ r\left(s_{N}\right) \end{array}\right]+\gamma\left[\begin{array}{ccc} p\left(s_{1} \mid s_{1}\right) & \cdots & p\left(s_{N} \mid s_{1}\right) \\ \vdots & \ddots & \vdots \\ p\left(s_{1} \mid s_{N}\right) & \cdots & p\left(s_{N} \mid s_{N}\right) \end{array}\right]\left[\begin{array}{c} v\left(s_{1}\right) \\ \vdots \\ v\left(s_{N}\right) \end{array}\right]\).

• \(\begin{aligned} v &=\mathcal{R}+\gamma \mathcal{P} v \\ (I-\gamma \mathcal{P}) v &=\mathcal{R} \\ v &=(I-\gamma \mathcal{P})^{-1} \mathcal{R} \end{aligned}\).

3. 강화학습 문제의 풀이 기법

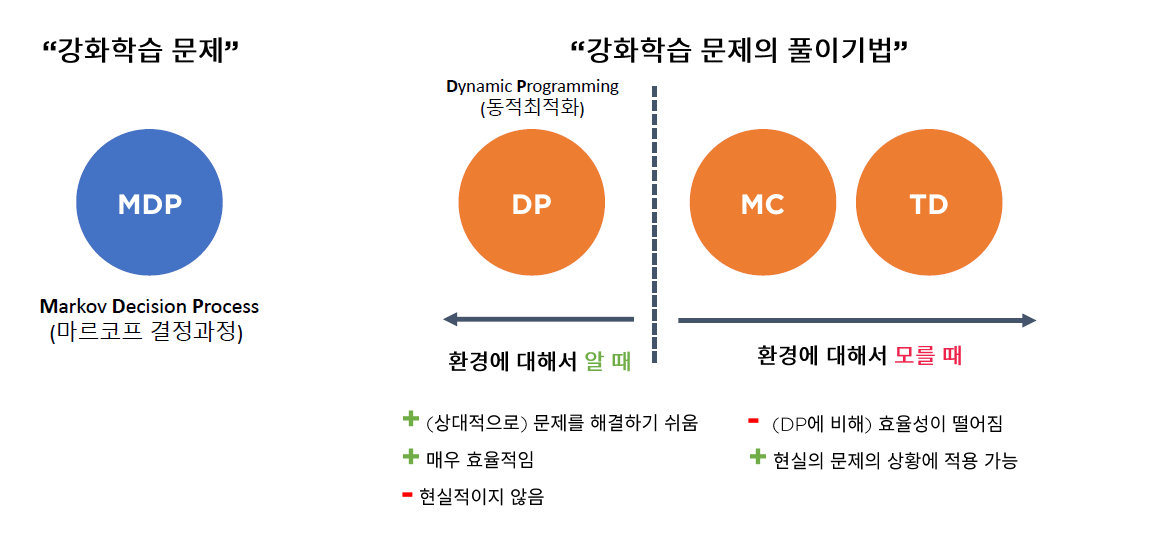
• MDP는 “환경에 대해 알 때” 푸는 방법론 중 하나임

4. MDP (Markov Decision Process)

우리는 특정 상태(state) \(S_t\)가 다음과 같으면 Markov Property를 가진다고 한다.

• \(P[S_{t+1} \mid S_t] = P[S_{t+1} \mid S_1,...,S_t]\).

즉, 미래의 상태(\(S_{t+1}\))는 지금 현재 상태(\(S_t\)) 만으로도 충분히 설명 가능하다는 것을 의미한다

(1) Markov Reward Process \(<S,P,R,\gamma>\)

Markov Reward Process : Markov Process의 각 state에 ‘reward’ 개념이 추가된 것

이 process는 다음과 같은 4개의 표현 \(<S,P,R,\gamma>\) 으로 나타낼 수 있다.

• 1 ) \(S\) : State의 집합
• 2 ) \(P\) : Transition Probability
  • \(P_{ss'}\) = \(P(s'\mid s) = P(S_{t+1}=s'\mid S_{t}=s)\) .
• 3 ) \(R\) : Reward의 집합
  • \(r(s) = E[R_{t+1}\mid S_t=s]\).
• 4 ) \(\gamma\) : 할인율

Example) MRP

.

(1) Terminal state

• Trap : \(R=-4\)
• Outside : \(R=1\)

(2) Reward :

• \(G_{t}=R_{t+1}+\gamma R_{t+2}+\ldots=\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1}\).

(3) Example : Room 1 \(\rightarrow\) Room 2 \(\rightarrow\) Outside

• \(G_{1}=-1+(0.5) \times(-2)+(0.5)^{2} \times 1=-1.75\).

(4) Time Complexity : \(O(n^3)\)

(5) 다른 solution : Iterative Solving Method

• Dynamic Programming
• Temporal Difference Learning
• Monte-Carlo Method

(2) Markov Decision Process \(<S,A,P,R,\gamma>\)

MDP = MRP + action (\(A\))

• \(\pi\) : Policy
  • 각 State에 대해, Action에 대한 확률 분포
  • \(\pi(a \mid s)=\mathbb{P}\left[A_{t}=a \mid S_{t}=s\right]\).
• \(P\) : Transition Probability
  • (MRP) \(P(s'\mid s) = P(S_{t+1}=s'\mid S_{t}=s)\)
  • (MDP) \(P_{\pi}\left(s^{\prime} \mid s\right)=\sum_{a \in A} \pi(a \mid s) P\left(s^{\prime} \mid s, a\right)\)
• \(R\) : Reward
  • (MRP) \(r(s) = E[R_{t+1}\mid S_t=s]\)
  • (MDP) \(r_{\pi}(s)=\sum_{a \in A} \pi(a \mid s) r(s, a)\)

(3) State-value function & Action-value function

• Policy (\(\pi\)) / Action (\(A\))를 고려한 value function
• state-value function : 어떠한 STATE가 더 많은 reward를 주는가?
• action-value function : 어떠한 STATE에서 어떠한 ACTION이 더 많은 reward를 주는가?

수식 비교

• (1) 상태 가치함수 / state-value function ( in MRP )
  • \(v(s)=\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) \mid S_{t}=s\right]\).
• (2) 행동 가치 함수 / state-value function ( in MDP )
  • \(\begin{aligned} v_{\pi}(s) &=\mathrm{E}_{\pi}\left[G_{t} \mid S_{t}=s\right]\\&=\mathrm{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right] \\ &=\sum_{a \in A} \pi(a \mid s)\left(r(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) v_{\pi}\left(s^{\prime}\right)\right) \end{aligned}\).
  • \(a\)에 dependent하지 않는다 ( 모든 \(a\)에 대해 expectation만 취할 뿐 )
• (3) action-value function
  • \(\begin{aligned} q_{\pi}(s, a) &=\mathrm{E}_{\pi}\left[G_{t} \mid S_{t}=S, A_{t}=a\right]\\&=\mathrm{E}_{\pi}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, A_{t+1}\right) \mid S_{t}=s\right] \\ &=r(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) \sum_{a \in A} \pi\left(a^{\prime} \mid s^{\prime}\right) q_{\pi}\left(a^{\prime} \mid s^{\prime}\right) \end{aligned}\).
  • \(a\)에 dependent

(4) Optimal solution

• optimal policy : \(\pi \geq \pi^{\prime} \text { if } v_{\pi}(s) \geq v_{\pi^{\prime}}(s), \forall s\)

• optimal state-value function : \(v_{*}(s)=\max _{\pi} v_{\pi}(s)\)
• optimal action-value function : \(q_{*}(s, a)=\max _{\pi} q_{\pi}(s, a)\)
• All optimal policies achieve the optimal state-value function
  • \[v_{\pi_{*}}(s)=v_{*}(s).\]
• All optimal policies achieve the optimal action-value function
  • \(q_{\pi_{*}}(s, a)=q_{*}(s, a)\).

( 앞으로, state-value function를 그냥 value function이라 부르겠다 )

(5) Bellman Optimality Equation (BOE, 벨만 최적 방정식)

\(V^{*}(s) =\sum_{a \in \mathcal{A}} \pi^{*}(a \mid s) Q^{*}(s, a) =\max _{a \in \mathcal{A}} Q^{*}(s, a)\).

\(Q^{*}(s, a) =R_{s}^{a}+\gamma \sum_{s, \in \mathcal{S}} P_{S S}^{a} V^{*}\left(s^{\prime}\right)\).

대입하고 나면….

$\begin{aligned} &V_{\pi}(s)=\max {a \in \mathcal{A}}\left(R{s}^{a}+\gamma \sum_{s \prime \in \mathcal{S}} P_{s s^{\prime}}^{a} V^{}\left(s^{\prime}\right)\right)
&Q_{\pi}(s, a)=R_{s}^{a}+\gamma \sum_{s^{\prime} \in \delta} P_{s s^{\prime}} a_{a, \epsilon_{\mathcal{A}}} Q_{\mathcal{A}}^{}\left(s^{\prime}, a^{\prime}\right) \end{aligned}$.

BOE의 특징

• 선형 방정식이 아님

• 일반해가 존재하지 않음

• iterative algorithm을 통해 계산하기

  ( ex. Policy Iteration, Value Iteration, Q-Learning, SARSA .. )

5. Summary

1. Bellman Equation : \(v(s)=\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) \mid S_{t}=s\right]\)

   ( solution : \(v =(I-\gamma \mathcal{P})^{-1} \mathcal{R}\) )

2. MRP & MDP

   • MRP : \(S\), \(P\), \(R\), \(\gamma\)

   • MDP : \(S\), \(P\), \(R\), \(\gamma\) + \(A\)

3. State-value function & Action-value function

   • state-value function : \(v(s)\) ( 혹은 \(v_{\pi}(s)\) )

     ( = value function 이라고도 부름 )

   • action-value function : \(q_{\pi}(s,a)\)

     ( = Q function 이라고도 부름 )