4.DP(1) Policy Iteration

[ 4. DP (1) Policy Iteration ]

Contents

1. Introduction
2. Planning vs Learning
3. Dynamic Programming
4. Policy Iteration
   1. Policy Evaluation
   2. Policy Improvement

1. Introduction

지난 포스트에서, 우리는 Markov Decision Process (MDP)에 대해서 배웠다. 우리는 최적의 \(\pi\)를 찾고 Reward를 구하기 위해, Bellman Equation을 사용하여 다음을 이끌어 냈었다.

• Value Function: \(v_{\pi}(s) = \sum_{a\in A} \pi(a\mid s)(R_s^a + \gamma \sum_{s' \in S} P^a_{ss'}v_{\pi}(s'))\)

• Action-Value Function : \(q_{\pi}(s,a) = R^a_{s} + \gamma \; \sum_{s' \in S} P^a_{ss'}v_{\pi}(s')\)

그리고 각각을 maximize하는 optimal solution을 구하는 것이 우리의 목표였다.

• \(v^{*}(s) = \underset{\pi}{max}\; v_{\pi}(s)\),

• \(q^{*}(s,a) = \underset{\pi}{max}\; q_{\pi}(s,a)\).

위의 optimal solution을 구하기 위해, 아래의 2가지 Dynamic Programming 방법을 사용할 것이다.

• 1 ) Policy Iteration
• 2 ) Value Iteration

이번 포스트에서는 그 중 첫번째인 1) Policy Iteration에 대해서 알아보고,

다음 포스트에서 2) Value Iteration에 대해 다룰 것이다.

2. Planning vs Learning

DP에 대해 알아보기 전에, Planning과 Learning이 무엇인지 알아보자.

(1) Planning : 모델에 대한 정보를 아는 경우 ( deterministic 환경 )

• 모델에 대한 정보?
  • environment에 대한 정보
  • State Transition matrix
• ex) MDP

(2) Learning : not Planning ( non-deterministic 환경 )

Process of Planning

(1) for Prediction

• input :
  • input 1) MDP + policy
  • input 2) MRP
• output : VALUE FUNCTION , \(v_{\pi}\)

(2) for Control

• input : MDP
• output : optimal value function \(v_{*}\) & optimal policy \(\pi_{*}\)

3. Dynamic Programming

Dynamic Programming ?

\(\rightarrow\) 풀고하자 하는 문제를 “여러 개의 작은 하위 문제”로 나눠서 푸는 것

Dynamic Programming의 조건

• 1 ) 하나의 문제를 “여러 개의 작은 문제”로 나눌 수 있어야!
• 2 ) 하나의 서브 문제를 풀고 난 뒤, 여기서 나온 솔루션을 “저장”할 수 있어야!

우리가 앞에서 배운 MDP(Markov Decision Process)는 이 두 조건을 만족한다.

MDP의 value function을 들여다 보면, \(v(s)\)를 구하기 위해, 그 안에 있는 \(v(S_{t+1})\)을 구하는 “Recursive 형태”를 보이는 것을 알 수 있다.

• \(v(s) = E[R_{t+1}+\gamma\;v(S_{t+1}\mid S_t = s)]\).

4. Framework of Policy Iteration

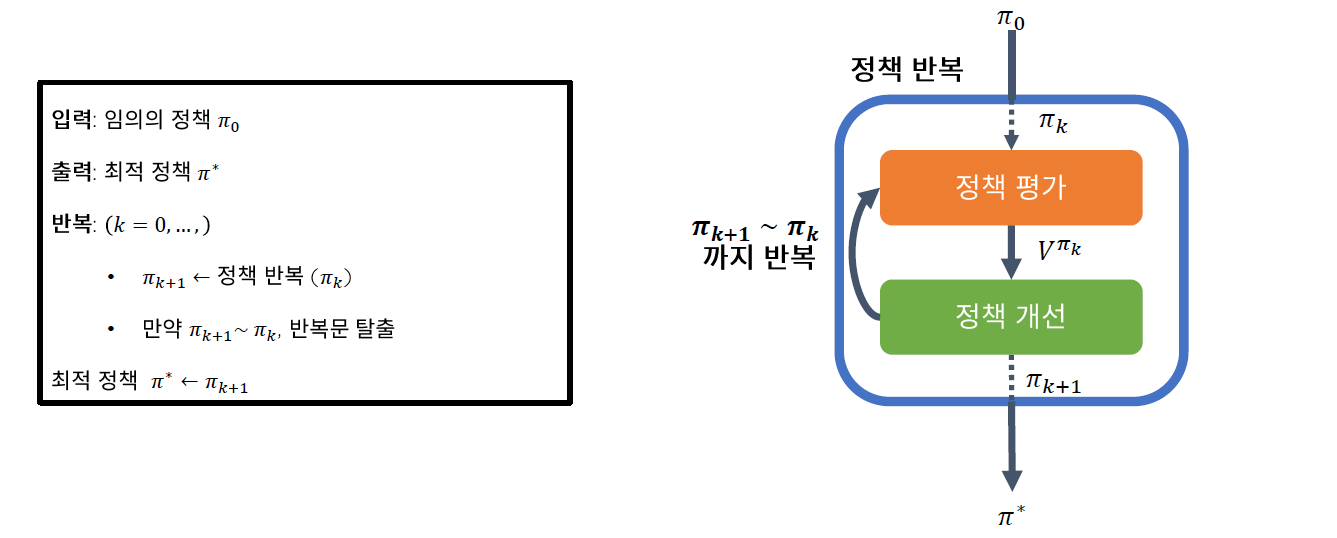
4. Policy Iteration

Policy Iteration은 다음과 같은 2가지 step이 iterative하게 이루어진다

• 1 ) Policy Evaluation
• 2 ) Policy Improvement

[ Algorithm ]

step 1) Initialize randomly

step 2) Repeat until convergence…

• ( Policy Evaluation ) let \(V = V_{\pi}\)

• ( Policy Improvement )

  for each state s, let \(\pi(s) = \underset{a\in A}{argmax}\; \gamma \sum_{s'\in S}^{ }P_{sa}(s')V^{*}(s')\)

return을 최대로 만드는 action을 선택하는 방향으로 계속 policy를 2가지 step이 iterative한 방식으로 update 해나가는 과정이다.

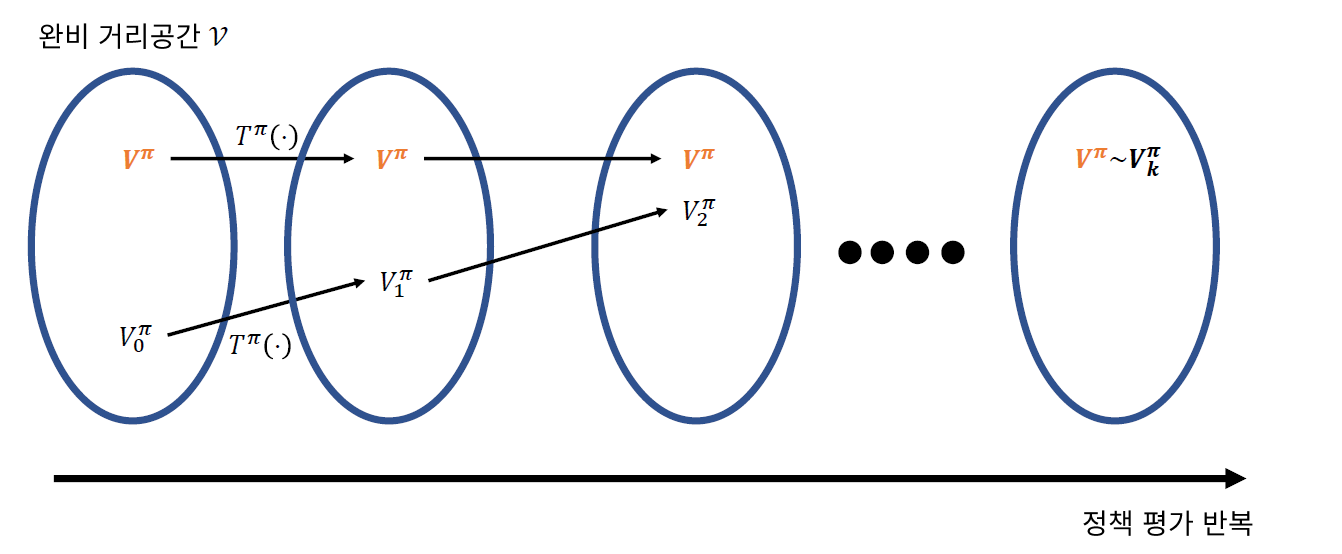
(1) Policy Evaluation

식으로 결론부터 이야기 하자면, 다음과 같이 policy \(\pi\)에서의 value를 구한다.

• \(v_{\pi}(s) = E[R_{t+1}+\gamma R_{t+2} + ... \mid S_t = s]\).

설명 및 예시

Policy evaluation, 말 그대로 ‘정책 평가’이다. 한 마디로, 현재 가지고 있는 policy에 따라 행동을 했을 경우, 각각의 state에서 agent가 얻게 되는 예상 return값들을 value로 계산하는 과정이다. 이를 통해, 최종적으로 이루고자 하는 것은 “각 state에서의 true value function 찾기“이다. 어떻게 그것을 이룰 수 있는지, 다음의 예시를 통해 알아보자.

[ Example ] ( https://t1.daumcdn.net/cfile/tistory )

위와 같이 4x4의 grid의 state가 있다고 가정하자. 현재 Agent는 왼쪽 상단(0,0)이나 오른쪽 하단(3,3)에 도착하면 게임을 종료한다. 한번 action을 취할 때마다 받게 되는 reward는 ‘-1’로, 쉽게 말해서 최소한의 움직임으로 현재 있는 위치에서 (0,0)이나 (3,3)에 도착을 해야 하는 것이다. 그리고 policy의 초기값으로, uniform random policy를 주어서 상하좌우로 움직일 확률을 각각 동일하게 1/4로 지정해준다. ( discount factor는 없다고 하자 )

이러한 environment에서, 만약 현재 Agent가 (1,2)에 있다고 했을 때, 이 Agent가 현재의 policy에 따라 행동을 했을 경우, 얻게 되는 value function V1(s)은 (위 수식 참고) -1이다. 이외 같은 방식으로 한번 iteration을 다 돈다. ( 즉, (0,0)~(3,3)까지의 이 과정을 계산한다 ) 단, iteration 중에, 하나의 state에서 다음 state로 넘어가면서 이전에 계산한 값은 지금 바로 update하지 않고, 그 값을 저장(기억)해 놓았다가 한 번의 iteration이 다 끝나고 나면 그때서야 전체적으로 update를 시행한다. 그렇게 되면, 최종 도착지인 (0,0)과 (3,3)을 제외한 나머지 14개의 state에서 value 값은 모두 -1이 되고, 이렇게 한번 iteration이 다 끝나면 이 값들을 (기존의 0에서) -1로 update해준다.


두 번째 iteration을 시행한다. (위 그림 참고) (1,2)위치에서는 V2(s)가 -1.75, (1,3)위치에서 V2(s)는 -2가 된다. ( 참고로, V 밑에 붙은 첨자는 현재 몇 번째 iteration을 진행하고 있는지를 의미한다 ) 이 iteration을 앞서서와 같은 방식으로 계속 반복하다 보면, 각 state에서의 value가 아래와 같이 update된다.

(2) Policy Improvement

식으로 결론부터 이야기 하자면, 다음과 같이 보다 최적의 \(\pi\)를 위해 update한다.

\[\pi(s) = greedy(v_{\pi}) = \underset{a\in A}{argmax}\; \gamma \sum_{s'\in S}^{ }P_{sa}(s')V^{*}(s')\]

설명 및 예시

policy improvement, 말 그대로 ‘정책 개선’이다. 앞선 예시에서, policy는 모든 state에서 상하좌우로 움직일 확률이 1/4이었다. 하지만 이는 당연히 최적의 policy일 리가 없고, 이를 optimal로 만들어 주기 위한 것이 바로 policy improvement이다. 그럼 어떻게 움직이는 것이 optimal일까? 우리는 앞선 단계 a.Policy Evaluation에서 각 state에서의 value function을 모두 구했다. 이것을 활용하여, 우리는 어떻게 다음 행동을 취해야 이것이 optimal하다고 할 수 있을지를 판단할 수 있다. 그 판단 기준은, 현재 agent가 속한 state에서 갈 수 있는 state들의 value이고, 이들 중 가장 value가 높은 곳으로 이동하는 것이바로 최적이 policy이다. 이 기준을 다음과 같은 식으로 나타낼 수 있다 (Q-value function,또는 action-value function)

\[q_\pi(s,a) = R_s^a + \gamma \sum_{s \in S}^{ } P_{ss'}^aV_\pi (s')\]

방금 얘기한 것을 앞선 예제를 통해 이해해보자.

state 1 ( (0,1) 위치 )에 있을 때, 상/하/좌/우로 움직였을 때의 return은 -15,-19,-1,-21이다. 그러면 우리는 이 상황(state)에서 Agent가 ‘왼쪽’으로 움직이는 것이 최적이다는 사실을 알 수 있다. 이 방식을 마찬가지로 state 5에도 적용했을 때, 이 곳에서도 마찬가지로 return이 가장 큰 ‘왼쪽’으로 움직여야 한다는 것을 알 수 있다.

이처럼, Policy Iteration은 (1) Policy Evaluation (각 state에서의 true value function 찾기)와 (2) Policy Improvement (각 state에서의 optimal policy 찾기)로 이루어진다. 지금까지 설명한 내용은 다음과 같이 아래 사진으로 요약할 수 있다.

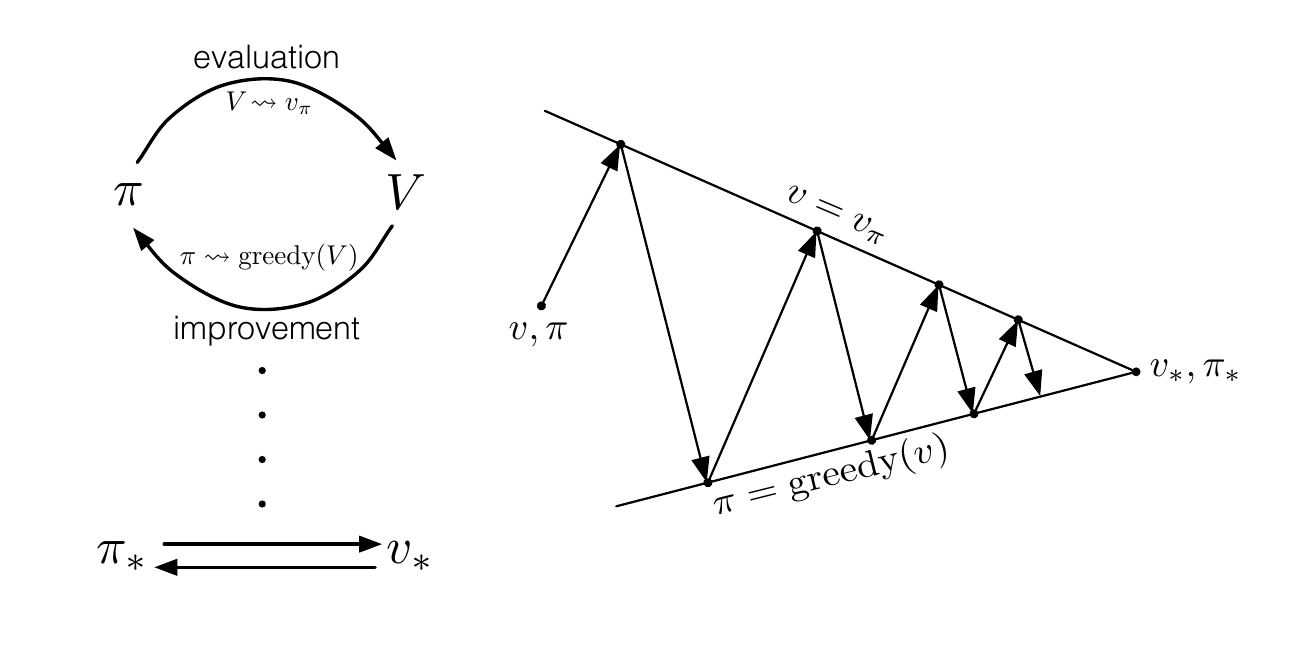
5. Summary

1. Planning vs Learning

   • Planning : 모델 정보 O ( ex. MDP )
   • Learning : 모델 정보 X ( ex. MC Learning, TD Learning )

2. Dynamic programming ( 여러 하위 문제로 나눠 풀기 )

   • (1) Policy iteration
   • (2) value iteration

3. Policy Iteration

   ( 아래 두 과정이 iterative하게 반복됨 )

   • step 1) policy EVALUATION ( EM 알고리즘의 E )
   • step 2) policy IMPROVEMENT ( EM 알고리즘의 M )