( 참고 : Fastcampus 강의 )
[ 7. DP (2) Value Iteration ]
1. Value Iteration
Policy Iteration은 아래의 두 step으로 이뤄짐을 확인했었다.
- ‘각 state에서의 value function을 찾아내는’ (1) Policy Evaluation과
- ‘각 state에서 optimal policy를 찾아내는’ (2) Policy Improvement
Dynamic Programming으로 MDP를 푸는 또 다른 방법인 Value Iteration의 알고리즘은 아래와 같다.

[ 알고리즘 ]
step 1) Initialize \(V(s)=0\), for all s
step 2) Repeat Until convergence
- \(V(s) = R(s) + \underset{a \in A}{max}\; \gamma \sum_{a'}^{ }P_{sa}(s')V(s')\) for all \(s\)
Policy vs Value Iteration
- Policy Iteration :
- value function을 구한 뒤, policy를 구한다
- 모든 value function을 구한 뒤, 이들을 모두 weighted sum ( 확률 고려하여 )
- Value Iteration :
- policy의 두 과정(evaluation&improvment)를 한번에 한다
- argmax를 통해, 하나의 최고 value function만을 greedy하게 선택
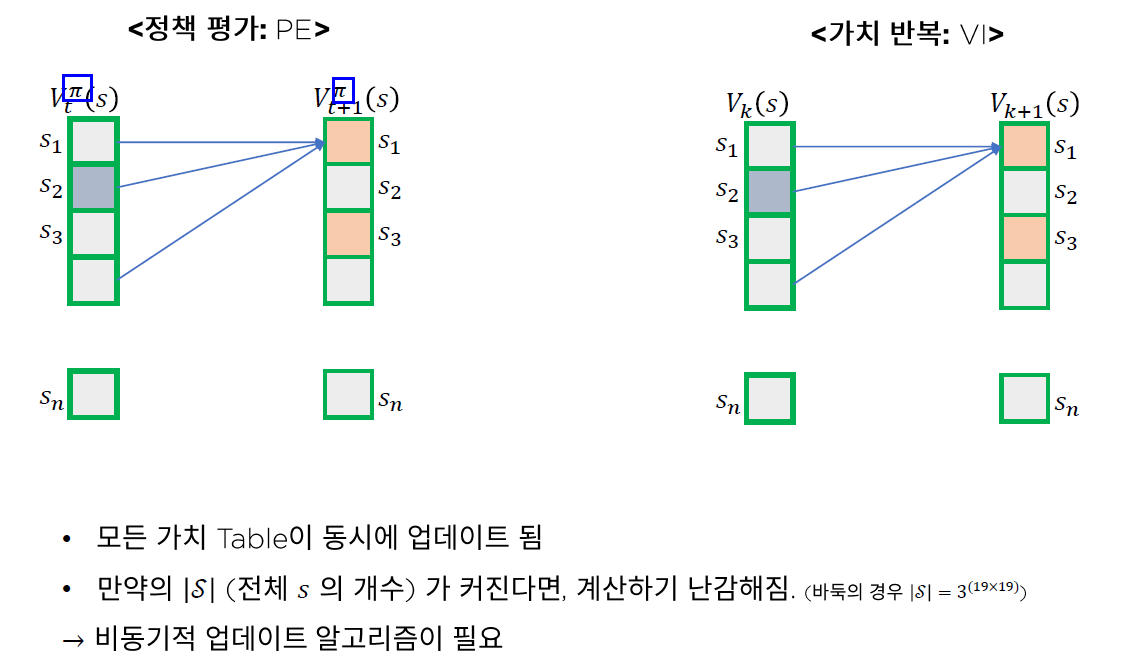
Example
-
( https://t1.daumcdn.net/cfile/tistory/99B8303A5A47731F10 )
위 그림을 통해서 알 수 있듯, 각각의 state는 해당 state에서 갈 수 있는 4개의 state들 중 max value를 자신의 value로 만든다. 이렇게 iteration을 여러 번 반복할 경우, 아래 그림과 같이 value들이 update된다.
2. 한계점
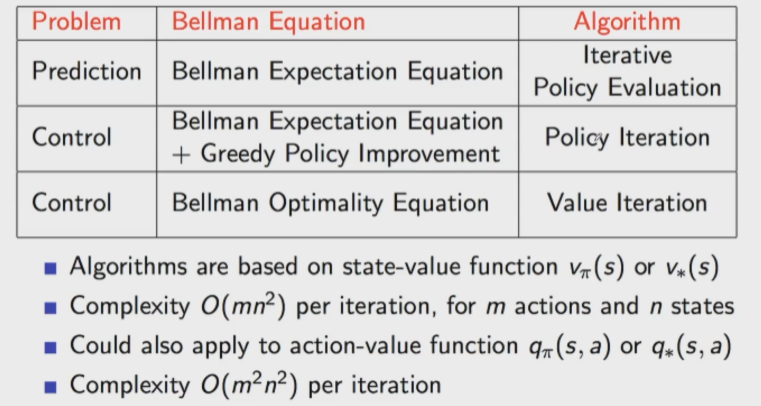
Policy Iteration과 Value Iteration과 같은 Dynamic Programming 방식은 엄청난 계산을 요한다. 위의 경우에는 4x4 grid이어서 간단해 보였을 수 있지만, 실제 세상에서는 이 방법을 통해서 문제를 푸는데에는 제약이 있다.
이어지는 포스트에서는 이러한 문제점을 보완하는 Monte Carlo Method에 대해서 알아보자.
3. Summary
-
Value Iteration :
-
\(V(s) = R(s) + \underset{a \in A}{max}\; \gamma \sum_{a'}^{ }P_{sa}(s')V(s')\).
-
하나의 최고 value function만을 greedy하게 선택 ( argmax )
( 즉, evaluation + improvement 한번에 수행 )
-
-
DP의 한계점 :
- 많은 계산량 ( 현실 세계는 continuous space )
- 이를 해결하기 위한 Monte Carlo 방법론


