12.Monte Carlo Learning

[ 12. Monte Carlo Learning ]

Contents

1. Introduction

2. Monte Carlo Approximation

3. MC Prediction
   1. DP vs MC
   2. Monte Carlo Prediction
   3. First visit method & Every visit method
4. MC Control
   1. Q-value Function
   2. Exploration
5. Summary

0. Review

환경에 대해 알 때? 모를 때?

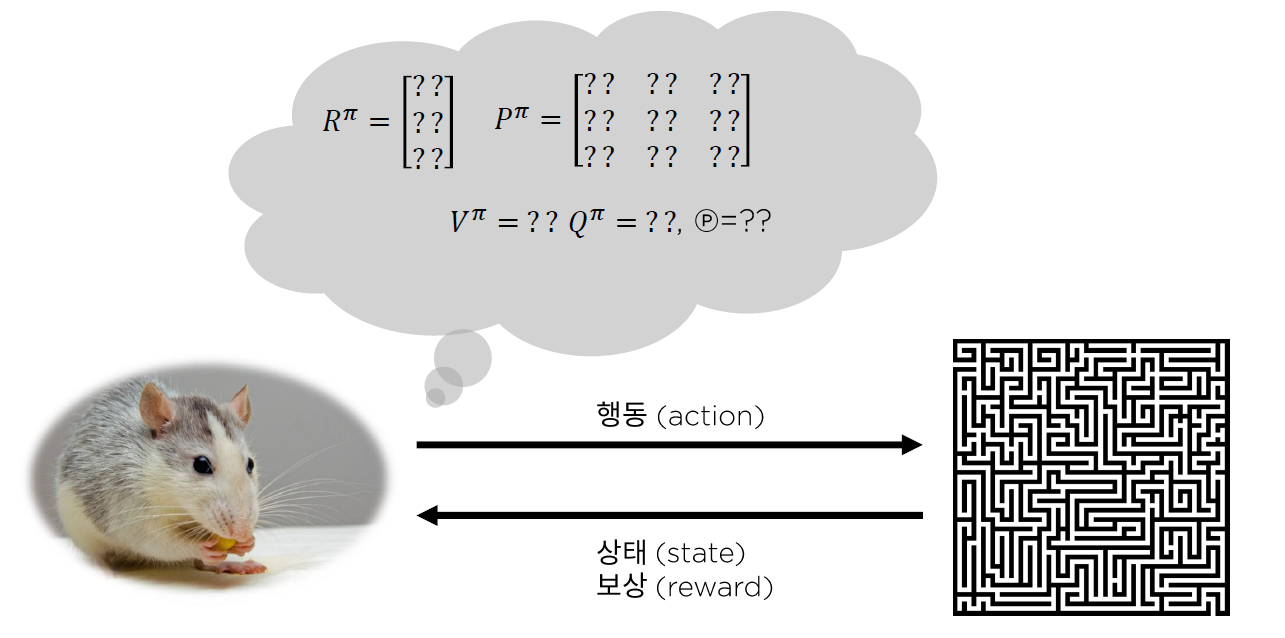
세상을 잘 모르는 쌩쥐

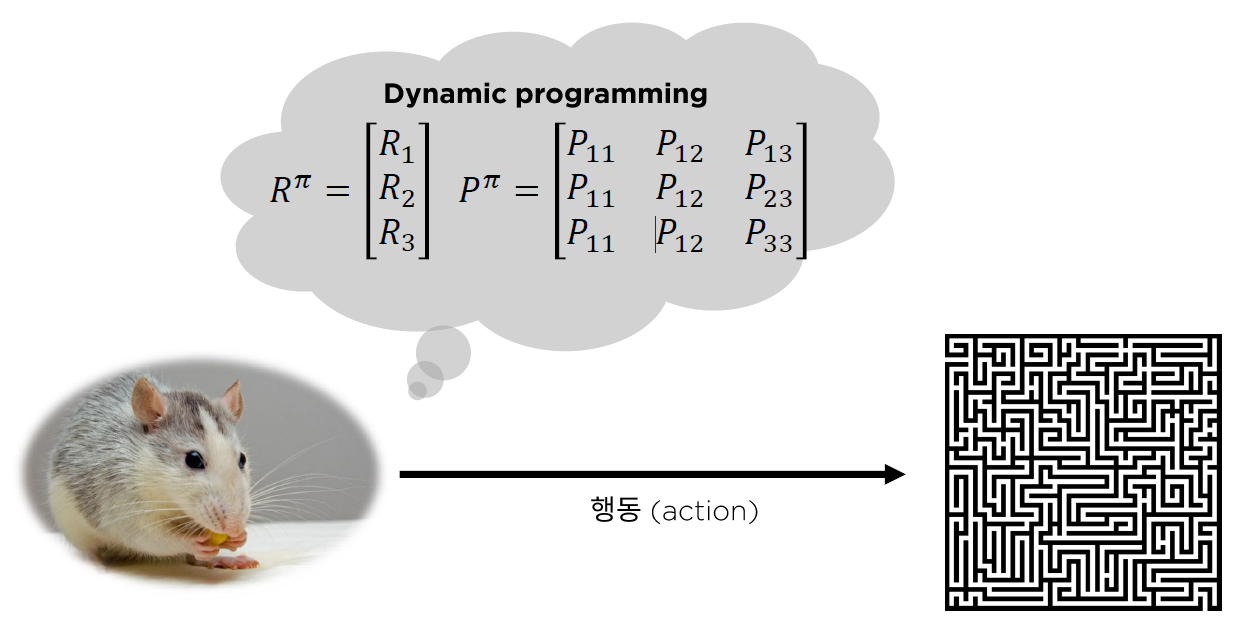
• 지금까지 앞에서 살펴봤던 알고리즘들 ( Planning )

세상을 잘 아는 쌩쥐

• 앞으로 살펴볼 알고리즘들 ( Learning )
• 현재 세상에 대한 지식을 가지고 있지 않기 때문에, 환경과의 상호작용을 통해 value function / policy / model을 inference한다.

1. Introduction

Planning vs Learning

• Planning : 모델에 대한 정보 O ( ex. Dynamic Programming)
• Learning : 모델에 대한 정보 X ( ex. MC Learning, TD Learning )

앞으로의 두 포스트에서 살펴 볼 방법들은 “Model-Free”한 방법들이다.

Model Free하다? ( = 모델에 대한 정보 X )

• MDP transition에 대한 사전 정보가 없음!
• Reward에 대한 정보도 없음!

Model-Free한 대표적인 두 가지 방법에는

• 1 ) Monte Carlo Learning
• 2 ) Temporal-Difference Learning 이 있다.

이 두 가지 Learning 방법들에 대해 각각의

• (1) Model Free Prediction : “Estimate” the value function of an unknown MDP
• (2) Model Free Control : “Optimize” the value function of an unknown MDP

에 대해 알아 볼 것이다.

그 중, 이번 포스트에는 Monte Carlo Learning의 Prediction과 Control에 대해 알아볼 것이다.

2. Monte Carlo Approximation

많이 들 알고 있겠지만, Monte Carlo Approximation에 대해 간략히 설명하게 넘어가겠다. 한 문장으로 요약하자면, “MC는 sampling을 통해 해를 찾는다(근사한다)”는 것을 의미한다.

Example

( https://kr.mathworks.com/matlabcentral/ )

위 그림 처럼 파란색 점과, 빨간색 점으로 이루어진 좌표를 보자. 여기서 우리는 파란색 점이 있는 부분의 넓이를 어떻게 구할까? y=x^2의 식으로 보여서, 적분을 통해서 쉽게 계산할 수 있겠지만, 확률을 이용하여 계산(엄밀히는 approximate)하는 방법이 있다. 임의의 점을 sampling하여, 해당 좌표에 아무렇게나 찍었을 때 그 점이 파란색 부분에 속할 확률을 구하면 (그 횟수는 충분해야할 것이다) \(25 \times 25 \times prob\) 통해 해당 부분의 넓이를 구할 수 있을 것이다. 이 쉬워보이는 개념이 Monte Carlo Approximation이다.

요약 : sampling을 통해 추정하고자 하는 값에 근사한다

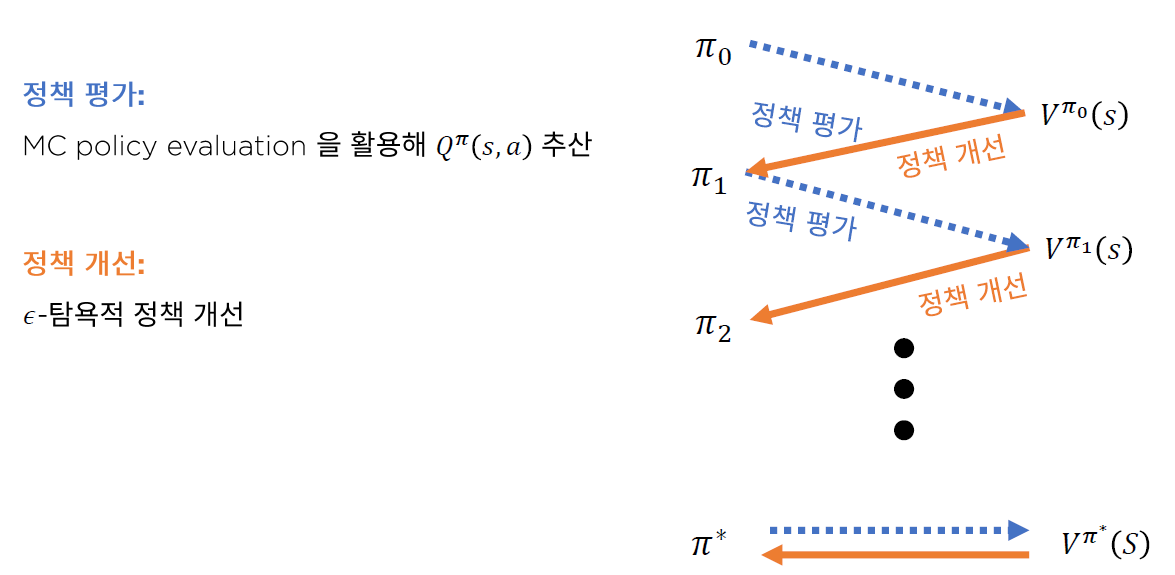
3. MC Prediction ( ESTIMATING value function )

( = Monte Carlo Policy Evaluation )

Episode : starting ~ terminal 까지의 과정

Reward :

\(\begin{array}{r} \mathrm{G}\left(\mathrm{s}_{1}\right)=R_{1}+\gamma R_{2}+\gamma^{2} R_{3}+\cdots \\ \mathrm{G}\left(\mathrm{s}_{2}\right)=R_{2}+\gamma^{2} R_{3}+\cdots \\ \mathrm{G}\left(\mathrm{s}_{3}\right)=R_{3}+\cdots \end{array}\).

(1) DP vs MC

• Dynamic Programming :

  \(v(s):=\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) \mid S_{t}=s\right]\).

• Monte Carlo Prediction :

  \(V_{\pi}(s) \sim \frac{1}{N(s)} \sum_{i=1}^{N(s)} G_{i}(s)\).

(2) Monte Carlo Prediction

\(\begin{aligned} V_{n+1} &=\frac{1}{n} \sum_{i=1}^{n} G_{i}=\frac{1}{n}\left(G_{n}+\sum_{i=1}^{n-1} G_{i}\right) \\ &=\frac{1}{n}\left(G_{n}+\sum_{i=1}^{n-1} G_{i}\right)=\frac{1}{n}\left(G_{n}+(n-1) \frac{1}{(n-1)} \sum_{i=1}^{n-1} G_{i}\right) \\ &=\frac{1}{n}\left(G_{n}+(n-1) V_{n}\right) \\ &=\frac{1}{n}\left(G_{n}+n V_{n}-V_{n}\right) \\ &=V_{n}+\frac{1}{n}\left(G_{n}-V_{n}\right) \quad \begin{array}{l} \end{array} \end{aligned}\).

Updating Equation

• \(V(s) \leftarrow V(s)+\frac{1}{n}(G(s)-V(s))\).

• step size \(\alpha\)의 incremental method

  \(V(s) \leftarrow V(s)+\alpha(G(s)-V(s))\).

(3) First Visit Method & Every Visit Method

First vs Every visit method

• First ) episode 상에서 “첫 방문” 했을 때만 update
• Every ) episode 상에서 “여러 방문” 했을 때 모두 update

4. MC Control ( OPTIMIZING value function )

( = Monte Carlo Policy Improvement )

이전에 배운 Policy Iteration은 크게 (1) policy evaluation과 (2) policy improvement로 나눠졌다.

여기서 (1) policy evaluation에, 그냥 위에서 배운 MC Approximation을 적용하면 MC Policy Iteration이 된다.

하지만 Monte Carlo 방법에도 여전히 다음과 같은 2가지 문제점이 존재한다.

(1) Value Function

• MDP와는 다르게, true value function을 구할 수 없다 ( sampling을 통해 근사할 뿐 )
• 모델에 대한 정보 X

(2) Local Optimum

• only sampling된 제한된 정보 하에서만 optimum!

그래서 이 두 문제를 해결하기 위해서 나온 것이 “Monte Carlo Control”이다.

Monte Carlo Control은…

• (1)번 문제 solution : value function 대신 action-value function ( = Q value function )을 이용
• (2)번 문제 solution : exploration을 이용하여 local optimum에 빠지게 될 위험을 줄임

(1) Q-value Function

기존의 (state) value function에 대한 greedy policy improvement를 위해서는, 아래의 model이 필요했었따.

( MDP의 경우, 다음과 같은 식을 통해 최적의 행동을 찾았다. )

• \(\pi'(s) = \underset{a \in A}{argmax}R_s^a + P^a_{ss'}V(s')\).

하지만, Q-value function에 대한 greedy policy improvement 의 경우, MODEL-FREE하다!

• \(\pi'(s) = \underset{a \in A}{argmax}Q(s,a)\).

(2) Exploration

\(\pi(a \mid s) = \left\{\begin{matrix} \epsilon / m + 1 - \epsilon \;\;\;\; if \; a^{*} = \underset{a\in A}{argmax}\;Q(s,a)\\ \epsilon / m \;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; otherwise \end{matrix}\right.\).

( \(m\) : 할 수 있는 행동의 가지 수 )

• EXPLOITATION : \(1-\epsilon\) 의 확률로 greedy action
• EXPLORATION : \(\epsilon\)의 확률로 random action

\(q_{\pi'}\) 에 대해 최적인 \(\epsilon-greedy\) policy \(\pi'\)는, 그 어떠한 \(\epsilon-greedy\) policy \(\pi\) 보다 크거나 같다.

이는 다음을 통해서 증명할 수 있다.

\[\begin{align*} q_{\pi}(s, \pi'(s)) &= \sum_{a\in A} \pi'(a \mid s)q_{\pi}(s,a)\\ &= \epsilon / m \sum_{a\in A}q_{\pi}(s,a) + (1-\epsilon)\underset{a \in A}{max}\;q_{\pi}(s,a)\\ &\geq \epsilon / m \sum_{a\in A}q_{\pi}(s,a) + (1-\epsilon)\sum_{a \in A}\frac{\pi(a\mid s) - \epsilon /m}{1-\epsilon}q_{\pi}(s,a)\\ &= \sum_{a\in A}\pi(a \mid s)q_{\pi}(s,a)\\ &= v_{\pi}(s) \end{align*}\]

Trick : \(\epsilon\)이 갈 수록 작아지게끔!

• 자주 사용하는 값 : \(\epsilon = \frac{1}{k}\), where \(k=\) episode index

5. Pseudo Code

지금 까지 배운 Monte Carlo를 요약하면, 다음과 같다.

우선 value-function대신 Q-value function (action-value function)을 사용한다는 점과, Monte Carlo Approximation 방법을 이용하여 일부를 sampling하여 진행한다는 점, 그리고 마지막으로 agent가 action을 선택할 때 의 확률로 exploration을 하여 local optimum에 빠질 위험을 줄인다는 것이 이 방법의 핵심이라 할 수 있다.

6. Summary

1. Model Free ( = 모델에 대한 정보가 없다 )

   • Learning 방법론 사용해야
   • ex) MC learning & Temporal Difference learning

2. Prediction & Control

   • 1) Prediction : value function을 ESTIMATE하기
   • 2) Control : value function을 OPTIMIZE하기

3. MC Prediction

   • value function을 approximate한다 ( via sampling )
   • (DP) \(v(s):=\mathbb{E}\left[R_{t+1}+\gamma v\left(S_{t+1}\right) \mid S_{t}=s\right]\)
   • (MC) \(V_{\pi}(s) \approx \frac{1}{N(s)} \sum_{i=1}^{N(s)} G_{i}(s)\)

   • updating equation : \(V(s) \leftarrow V(s)+\alpha(G(s)-V(s))\)

   • update하는 빈도에 따라 First & Every Visit method

4. MC Control

   • DP에서 했던거에 단지 MC 적용하면 될까? NO! 문제점?
     • 문제 1) true value function 구할 수 없음
     • 문제 2) local optimum
   • 해결 1) Q-value function ( = action-value function ) 사용
   • 해결 2) Exploration (\(\epsilon\) greedy)