16.Time Difference Learning (2)

( 참고 : Fastcampus 강의 )

[ 16. Time Difference Learning (2) ]

Review : N-step TD

\(G_t^{(n)} = R_{t+1} + \gamma \; R_{t+2} + ... + \gamma^{n-1}R_{t+n} + \gamma^n V(S_{t+n})\).

\(V(S_t) \leftarrow V(S_t) + \alpha (G_t^{(n)}- v(S_t))\).

\(TD(\lambda)\) : 여러 개의 N-step들의 return을가중평균하여 \(G_t\)로 사용 하는 방법이

1. \(TD(\lambda)\)

ex) 간단한 예로, 2-step과 4-step의 \(G\)를 단순평균하여 사용한다면, 다음과 같이 될 것이다.

• \(\frac{1}{2} G^{(2)} + \frac{1}{2}G^{(4)}\).

어떻게 하면, 여러 개의 time-step의 return들을 적절히 가중평균할 수 있을까?

( how to set WEIGHT? 우선, \(\lambda\) (weight)는 time이 갈 수록 discount 되게! )

(1) Forward-view \(TD(\lambda)\) : n-step TD

위 식을 보면, step 1에서는 \((1-\lambda)\)만큼의 weight를, 그 이후로는\((1-\lambda)\lambda\), 또 그 이후로는 \((1-\lambda)\lambda^2\)…처럼 갈수록 weight가 줄어드는 (\(\lambda\)는 0 ~ 1사이 값)식으로 가중치를 부여한다. ( = 각 time step의 return 앞에 붙는 weight 값들의 합은 1이 된다. )

\(\lambda\)가 작을 수록, 최근 (recent)에 더 큰 가중치를 둔다.

이 방법은 TD(0)와는 다르게, “모든 time step의 return값”들을 반영할 수 있다는 장점이 있다.

하지만, 이 방법은 결국 Monte Carlo처럼 “episode가 한번 다 끝나야 update”가 이루어진다. 이는 곧 Time Difference가 본래 추구하고자 했던 “online update가 불가능”해진다는 단점이 있다.

(2) Backward-view \(TD(\lambda)\) : eligibility trace

[Q]. online으로 update가 되도록 만들 수 없을까?

Forward view와는 다르게, episode가 다 끝나지 않아도 incomplete sequence으로 부터 online으로 update할 수 있는 방법이다. 이를 이루기 위해, “Eligibility trace”를 도입한다.

Eligibility trace에 대해 알아 보기 전에, 아래의 두 개념에 대해 알아보자.

• Frequency heuristic : “자주” 발생하는 state에 credit 부여!

• Recency heuristic : “최근”에 발생한 state에 credit 부여!

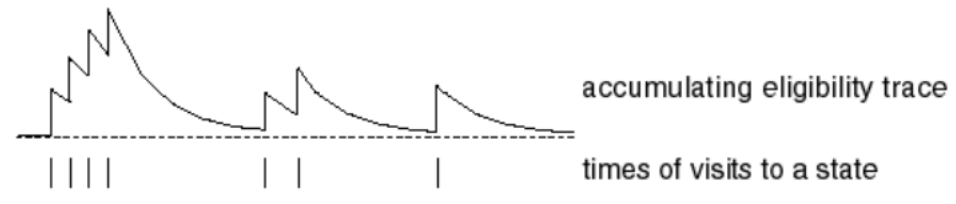
Eligibility trace는 위의 두 개념을 모두 반영한다.

• \(E_{0}(s)=0\).
• \(E_{t}(s)=\gamma \lambda E_{t-1}(s)+\mathbf{1}\left(S_{t}=s\right)\).
• 매 time step마다 eligibility trace \(E_t(s)\)를 계속 측정한다

updating equation : \(V(S_t) \leftarrow V(S_t) + \alpha \delta_t\;E_t(s)\)

• where \(\delta_t = R_{t+1}+\gamma\;V(S_{t+1}) - V(S_t) \;\;(= TD\; error)\)

위 식을 보면, frequency heuristic를 반영하기 위해 이전에 방문한 적이 있던 state면 ‘+1’을 주는 것을 확인할 수 있다. 또한, recency heuristic을 반영하는 \(\gamma\) 가 있음을 알 수 있다. 이렇게 해서 구한 eligibility trace를 TD error에 곱한 뒤 update를 한다. 이런 식으로, 매 state마다 eligibility trace를 계산 하고 \(V(s)\)를 update한다.

[ Theorem ]

sum of offline updates is identical to forward view & backward view TD(\(\lambda\))

• \(\sum_{t=1}^{T} \alpha \delta_{t} E_{t}(s)=\sum_{t=1}^{T} \alpha\left(G_{t}^{\lambda}-V\left(S_{t}\right)\right) \mathbf{1}\left(S_{t}=s\right)\).

2. Summary

1. TD(\(\lambda\)) : n-step들을 가중평균

2. $\lambda$가 클 수록, 현재가 더 중요

3. Backward-view & Forward View

   • 1) Backward-view TD(\(\lambda\))

     • 모든 시점을 다 사용 시, TD의 본래 목적인 “online update가 불가능”

   • 2) Forward-view TD(\(\lambda\))

     • eligibility trace ( online으로 만들어주기 위해 )

       • 1) frequency heuristic
       • 2) recency heuristic

     • updating equation : \(V(S_t) \leftarrow V(S_t) + \alpha \delta_t\;E_t(s)\)

       where \(\delta_t = R_{t+1}+\gamma\;V(S_{t+1}) - V(S_t) \;\;(= TD\; error)\)