20.Off-policy MC Control

( 참고 : Fastcampus 강의 )

[ 20. Off-policy MC Control ]

Contents

1. Review
2. Off policy의 장점
3. Off policy 학습
   1. 목적
   2. Example
   3. Importance Sampling
   4. 구체적 알고리즘

1. Review

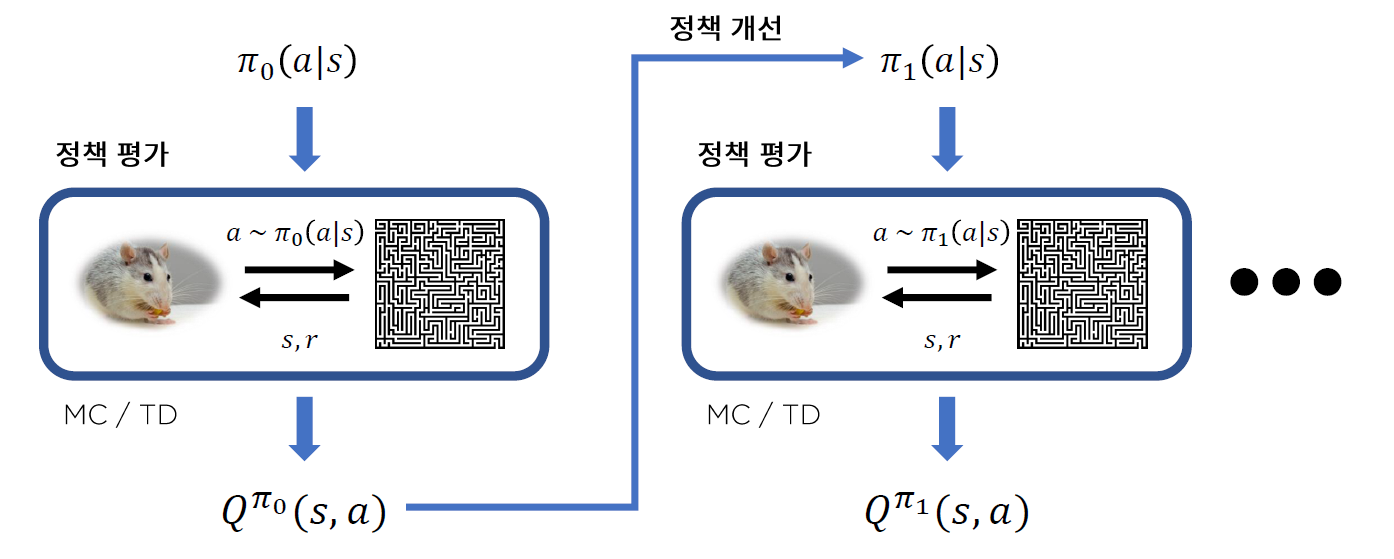
• 0) 임의의 Policy \(\pi_0\) 에서 시작

• 1) Agent와 Environment사이의 상호작용 ( action & state/reward 받기 )

• 2) Q값 추산

• 3) 정책 개선 (epsilon-greedy)하여 \(\pi_1\)로 update

• 1) Agent와 Environment사이의 상호작용 ( action & state/reward 받기 )

• 2) Q값 추산

  ….

문제점 : 매 정책 개선마다, \(Q^{\pi_k}\)를 계산하기 위해 새로운 샘플이 필요하다! INEFFICIENT

Off Policy?

사람은, 자신이 한 행동이 아니라도, 자신의 행동을 더 개선시킬 수 있다.

RL의 agent또한 그럴 수 있다. 이러한 학습 scheme을 Off-policy라고 한다!

Goal

• 목표 : 주어진 정책 \(\pi(a \mid s)\)에 대한 \(Q^{\pi}(s,a)\)를 계산하는 것
  • \(\pi(a \mid s)\) : TARGET policy
• 의문점 : 임의로 정한 행동 정책 \(\mu(a \mid s)\)으로 구한 episode에서도, \(Q^{\pi}(s,a)\)를 계산할 수 있을까?
  • \(\mu(a \mid s)\) : BEHAVIOR policy
  • 정답 : YES! OFF Policy

2. Off policy의 장점

3. Off policy 학습

(1) 목적

\(Q^{\pi}(s,a)\) 를 잘 추산하기

\(\rightarrow \quad \because\) 좋은 policy를 찾을 수 있으므로

\(\begin{aligned} Q^{\pi}(s, a) & \stackrel{\text { def }}{=} \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right] \\ &=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\ldots \mid S_{t}=s, A_{t}=a\right] \end{aligned}\).

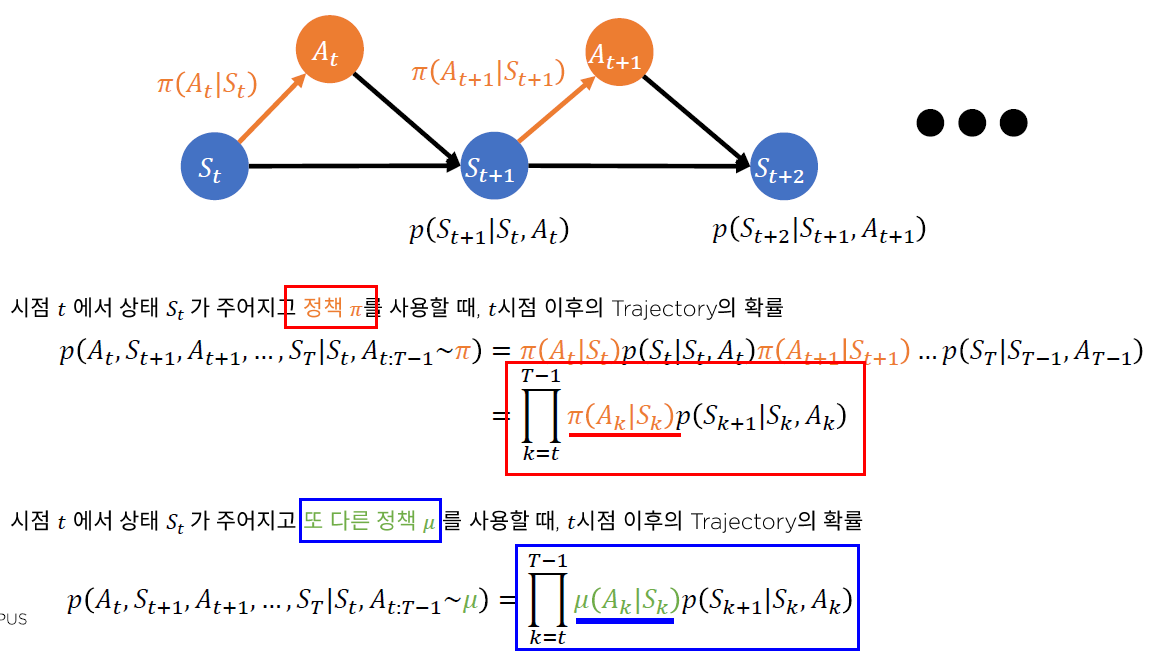
위 notation에서 \(\pi\)의 의미?

• 정책 \(\pi\)를 따를 경우, 발생할 trajectory의 분포에 대하나 expectation값!

(2) Example

(3) Importance Sampling

WHEN? \(p(x)\)에 대한 evaluation은 가능하나, sampling이 어려울 때!

HOW? 보다 쉬운 (sampling이 가능한) \(q(x)\)를 사용하여 \(\mathbb{E}_{x \sim P}[f(x)]\)를 추산하기

\(\begin{aligned} \mathbb{E}_{x \sim P}[f(x)] &=\sum_{x \in X} p(x) f(x) =\sum_{x \in X} q(x) \frac{p(x)}{q(x)} f(x) =\mathbb{E}_{x \sim Q}\left[\frac{p(x)}{q(x)} f(x)\right] \end{aligned}\).

위 방법론을, 우리의 Q함수에 적용할 경우 아래와 같다.

\(\begin{aligned} Q^{\pi}(s, a) & \stackrel{\text { def }}{=} \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right] \\ &=\mathbb{E}_{\mu}\left[\rho_{t: T-1} G_{t} \mid S_{t}=s, A_{t}=a\right] \end{aligned}\).

(4) 구체적 알고리즘

a) Key Idea : 임의의 행동 정책함수 \(\mu\)로 episode 생성 후 학습

b) Importance Sampling 개념 사용하여 아래를 계산

• \(G_{t}^{\pi / \mu}=\prod_{k=t}^{T-1} \frac{\pi\left(A_{k} \mid S_{k}\right)}{\mu\left(A_{k} \mid S_{k}\right)} G_{t}\).
  

c) MC-update 식 :

• \(Q\left(s_{t}, a_{t}\right) \leftarrow Q\left(s_{t}, a_{t}\right)+\alpha\left(G_{t}^{\pi / \mu}-Q\left(s_{t}, a_{t}\right)\right)\).
  

d)문제점?

• \(\prod_{k=t}^{T-1} \frac{\pi\left(A_{k} \mid S_{k}\right)}{\mu\left(A_{k} \mid S_{k}\right)}\) 때문에, \(G_{t}^{\pi / \mu}\) 의 분산이 커질 수 있음. ( variance reduction needed! )

• variance를 최소화 하는 \(\mu^{*}\)를 찾을 수 있긴 하지만,

  • 1) \(\mu^{*}\)를 찾아야 하는 추가적인 노력 필요
  • 2) 그렇게 해서 찾게 된 \(\mu^{*}\)가 exploration에 도움이 되지 않을 수도

  \(\rightarrow\) 현실적으로 Off-policy MC가 잘 사용되지 않는 이유임.