27.Policy Gradient (REINFORCE)

( 참고 : Fastcampus 강의 )

[ 27. Policy Gradient (REINFORCE) ]

Contents

1. Review
2. Policy Gradient
   1. Policy Gradient 간략 소개
   2. 정책 판단 기준, \(J(\theta)\)
   3. Gradient Ascent of \(J(\theta)\)
   4. \(\nabla_{\theta} J(\theta)\) 를 쉽게 계산하는 법 ( = Sampling )
3. REINFORCE
4. REINFORCE + Batch Update
5. Variance Reduction Technique, “Baseline”
   1. Baseline
   2. Return 표준화

1. Review

(1) 가치 기반 강화학습

아래의 step으로 최적의 policy를 찾았다.

Data + Policy Evaluation/Improvement \(\rightarrow\) \(Q^{\pi}(s,a)\) 추정 \(\rightarrow \pi(a \mid s)\) 찾기

( 즉, 행동가치 함수 \(Q^{\pi}(s,a)\)를 사용하여 정책을 만들었었다 )

위 방식의 단점?

• 1) action space의 크기 \(\mid A \mid\) 가 너무 클 경우, 학습 hard

  ( 이전에 봤던 문제들은 \(\mid A \mid\)가 4, 2 였던 simple한 상황 )

• 2) continuous action space를 다루기 어렵다

  ( ex. 드론이 상/하/좌/우 4가지 방향으로만 움직이지는 않는다 )

• 3) 정책이 deterministic하다 ( \(\neq\) stochastic )

  ( 가위바위보의 최적 정책은, 각 행동을 1/3로 했을 때 )
  

Data로 부터, ( \(Q^{\pi}(s,a)\) 없이 ) 곧 바로 정책을 만들면 어떨까?

\(\rightarrow\) Policy Gradient

2. Policy Gradient

(기존) : Data + Policy Evaluation/Improvement \(\rightarrow\) \(Q^{\pi}(s,a)\) 추정 \(\rightarrow \pi(a \mid s)\) 찾기

(PG) : Data + Policy Gradient \(\rightarrow \pi(a \mid s)\) 찾기

(1) Policy Gradient 간략 소개

• step 1) 정책 함수 \(\pi_{\theta}(a \mid s)\)를 판단하는 기준 \(J(\theta)\)를 설정

• step 2) \(J(\theta)\)에 대한 gradient ( = policy gradient )를 계산

• step 3) Gradient ASCENT를 통해 policy를 optimize

(2) 정책 판단 기준, \(J(\theta)\)

\(J(\theta)=V^{\pi_{\theta}}\left(s_{0}\right)\).

• \(s_0\) : 고정된 시작 상태
• 의미 : 정책 함수 \(\pi_{\theta}(a \mid s)\) 에 대한 \(s_{0}\) 의 TRUE 상태 가치함수 값
• \(V^{\pi_{\theta}}\left(s_{0}\right) = \mathbb{E}_{\pi_{\theta}}\left[G_{0} \mid S_{0}=s_{0}\right]\).

(3) Gradient Ascent of \(J(\theta)\)

\(\nabla_{\theta} J(\theta)=\nabla_{\theta} V^{\pi_{\theta}}\left(s_{0}\right)=\nabla_{\theta} V^{\pi}\left(s_{0}\right)\) ( notation \(\theta\) 생략 )

위의 gradient는, 아래와 같이 recursive한 구조로 이루어짐을 알 수 있다.

위 식을 재정리하면…

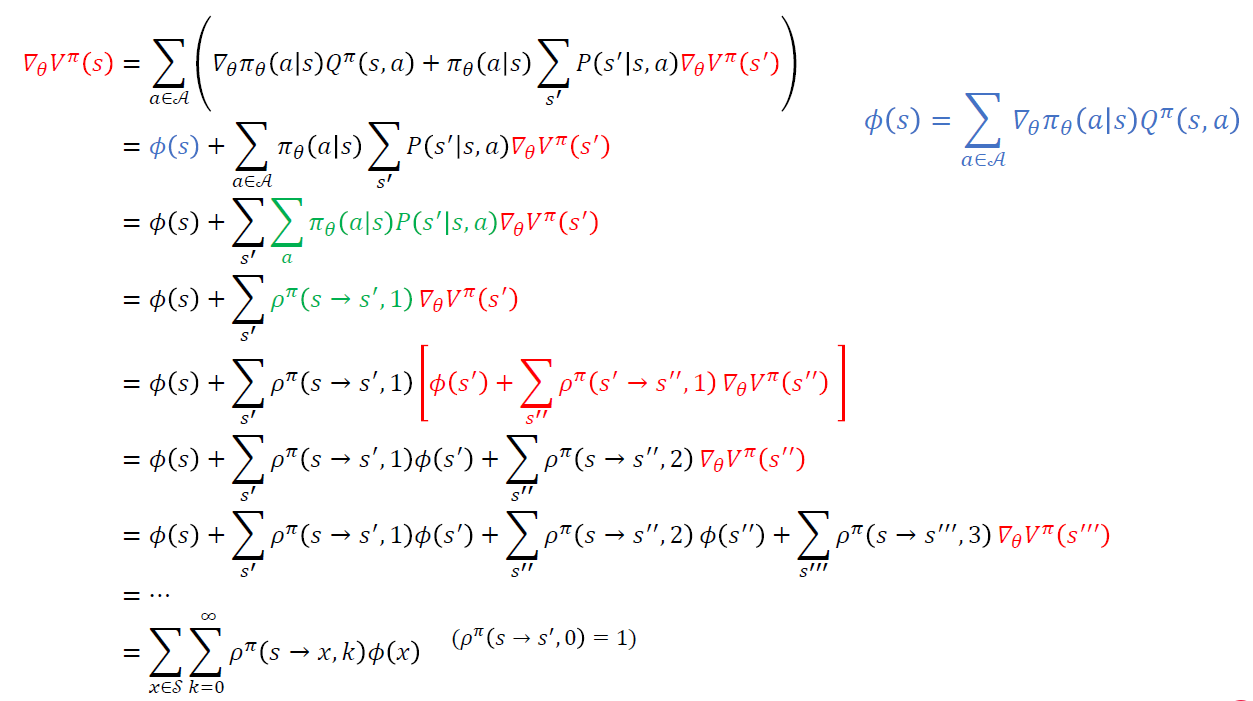
* 위 식에서 \(\rho^{\pi}(s \rightarrow s^{'},1)\)의 의미 :

• \(s\)에서 \(s^{'}\)으로 1번의 transition만에 도착할 확률

* 위 식에서 \(\rho^{\pi}(s \rightarrow s^{''},2)\)의 의미 :

• \(s\)에서 \(s^{''}\)으로 2번의 transition만에 도착할 확률 ( 중간에 어떠한 state를 거치든 무관 )

위 식을 마지막으로 정리하자면, 아래와 같다.

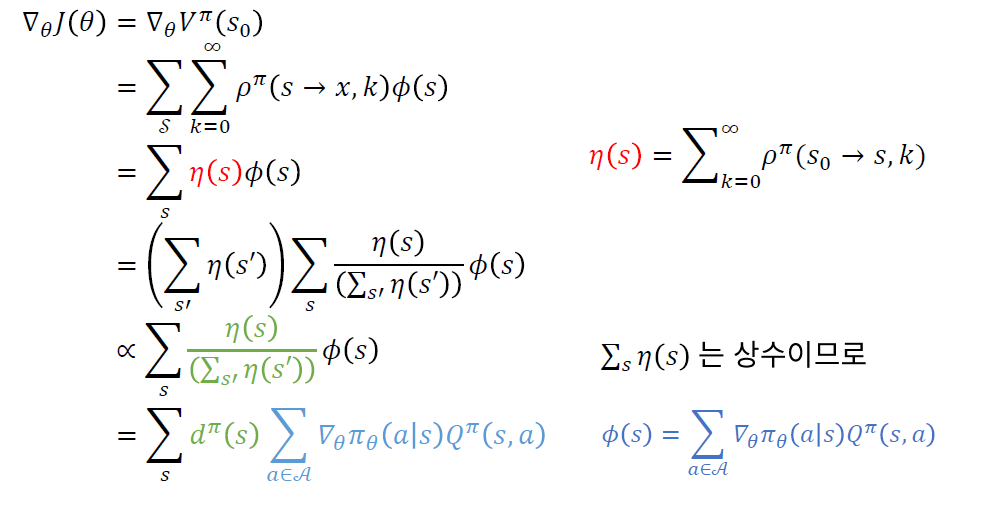
* 위 식에서, \(d^{\pi}(s)=\lim _{t \rightarrow \infty} P\left(s_{t}=s \mid s_{0}, \pi_{\theta}\right)\) 의 의미 :

• stationary distribution ( of states )
• 아주 긴 시간 이후에, 각 state에 방문할 확률
• initial state와는 무관하다!

(4) \(\nabla_{\theta} J(\theta)\) 를 쉽게 계산하는 법 ( = Sampling )

Importance Sampling 방법을 사용하자!

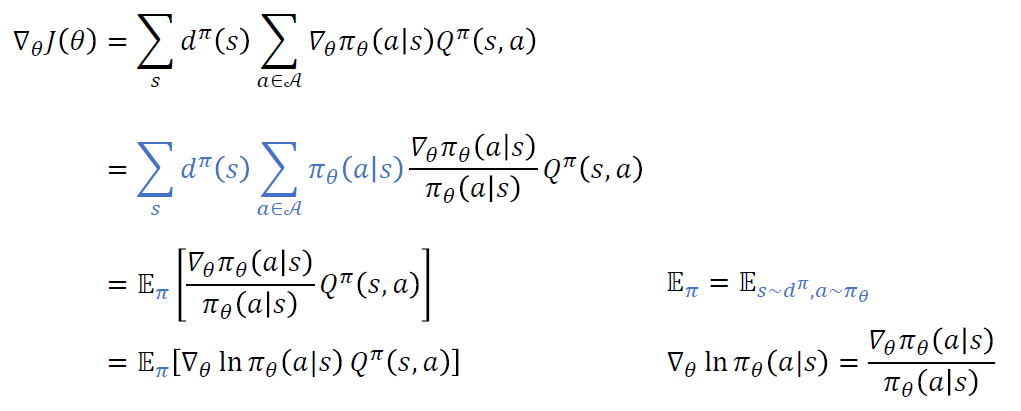
3. REINFORCE

위의 2. Policy Gradient의 결론으로 구했던 \(\nabla_{\theta} J(\theta)\)는 아래와 같았다.

\(\begin{aligned} \nabla_{\theta} J(\theta) &=\mathbb{E}_{\pi}\left[\nabla_{\theta} \ln \pi_{\theta}(a \mid s) Q^{\pi}(s, a)\right] \\ &=\mathbb{E}_{\pi}\left[\nabla_{\theta} \ln \pi_{\theta}\left(A_{t} \mid S_{t}\right) G_{t}\right] \end{aligned}\).

( \(\because\) \(Q^{\pi}(s, a) \stackrel{\text { def }}{=} \mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s, A_{t}=a\right]\) )

여기서 \(G_t\) 를, Monte Carlo 방법으로 추정한다! 이를 활용한 방법이 REINFORCE이다.

(vanilla) REINFORCE 알고리즘은 아래와 같다.

( = 매 time step 마다 update가 이루어진다 )

4. REINFORCE + Batch Update

위의 3.REINFORCE에서는, 매 time step 마다 update가 이루어졌지만, 이를

• 1) 매 episode 마다
• 2) 여러 episodes 마다

update를 이루어지게끔 할 수도 있다.

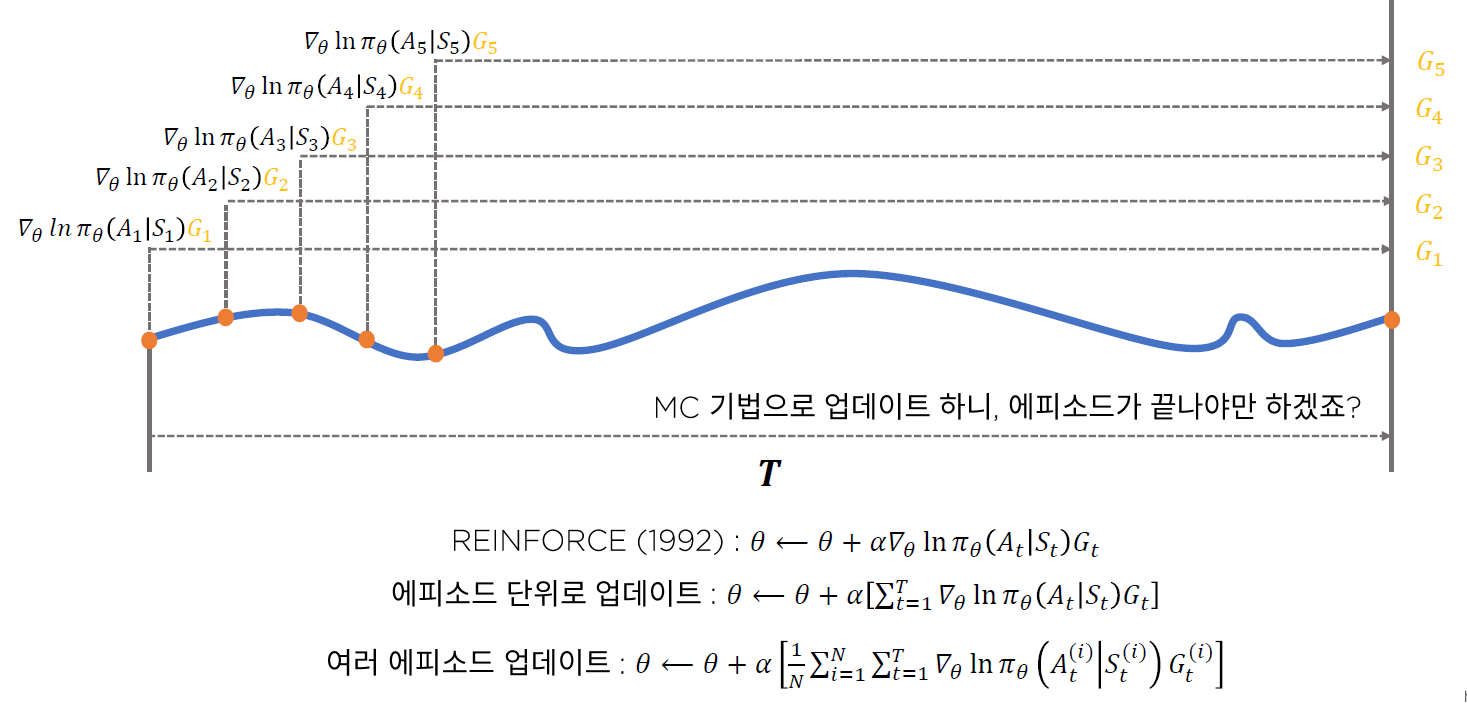
하지만, 위 방법들에는 문제점이 있다. ( 사실, MC를 사용하는 모든 방법론의 문제점이라고 할 수도 있다 )

바로 variance가 커지는 문제이다. 따라서 이 문제를 보완하기 위해 TD n-step을 사용하기도 했었다.

REINFORCE에서도 마찬가지로 이를 해결해야는 상황인데, 그러기 위해서 자주 사용하는 방법이 바로 baseline만큼을 빼주는 것이다.

5. Variance Reduction Technique, “Baseline”

(1) Baseline

Baseline은 딱 하나의 값으로 정해진 것이 아니다.

행동 \(a\)에 대해 독립적인 함수이면, 뭐든 빼줘도 지장이 없다 ( = 뭐든 baseline으로 설정할 수 있다 )

하지만 우리는 그 중에서도, variance를 가장 잘 줄여줄 수 있는 baseline을 찾는 것이 중요하다.

( 기존 )

• \(\nabla_{\theta} J(\theta) \propto \sum_{s} d^{\pi}(s) \sum_{a \in \mathcal{A}} \nabla_{\theta} \pi_{\theta}(a \mid s) Q^{\pi}(s, a)\).

( Baseline 차감 )

• \(\nabla_{\theta} J(\theta) \propto \sum_{s} d^{\pi}(s) \sum_{a \in \mathcal{A}} \nabla_{\theta} \pi_{\theta}(a \mid s)\left(Q^{\pi}(s, a)-b(s)\right)\).

where \(\sum_{a \in \mathcal{A}} \nabla_{\theta} \pi_{\theta}(a \mid s) b(s)=b(s) \nabla_{\theta} \sum_{a \in \mathcal{A}} \pi_{\theta}(a \mid s)=b(s) \nabla_{\theta} 1=0\).

(2) ex) Return 표준화

하나의 Trajectory 내의 return들 : \(G=\left\{G_{1}, G_{2}, G_{3}, \ldots, G_{T}\right\}\)

Standardize : \(G_{t}^{*}=\frac{G_{t}-\bar{G}}{\sigma(G)}\)

• mean : \(\bar{G}=\frac{1}{T} \sum_{t=1}^{T} G_{t} \quad\)
• stdev : \(\sigma(G)=\sqrt{\frac{1}{T} \sum_{t=1}^{T}\left(G_{t}-\bar{G}\right)^{2}}\)

결론 : \(\theta \leftarrow \theta+\alpha \gamma^{t} G_{t}^{*} \nabla_{\theta} \ln \pi_{\theta}\left(A_{t} \mid S_{t}\right)\)