39.(paper 4) DDQN,TD3 for Maximization Bias

( 참고 : Fastcampus 강의 )

[ 39.(paper 4) DDQN,TD3 for Maximization Bias ]

1. Introduction

( Maximization Bias를 해결하기 위한 다음의 방법들을 알아볼 것임 )

[1] Maximization Bias in “Q-Learning”을 해결하기 위해…

• Double Q-Learning
• Deep Double Q-Learning (DDQN)
  

[2] Maximization Bias in “Actor-Critic”을 해결하기 위해…

• Addressing Function Approximation Error in Actor-Critic Methods (TD3)

2. Maximization Bias란?

https://seunghan96.github.io/rl/36.(paper2)DQN%EA%B0%9C%EC%84%A0/ 참고하기

3. (Q-Learning) DDQN

DDQN (Deep Double Q-Learning) = Double Q-Learning + DQN

Q-Learning에서 maximization bias가 발생하는 이유?

• 1) MDP의 stochasticity ( 위의 2.블로그 참조 )

• 2) Insufficiently flexible function approximation

  The main contribution of Van Hasselt et al. was to show that the overestimation can happen in cases like Atari 2600 with ANNs as well, where function approximators are flexible (Universal Approximation Theorem) and stochasticity is very less (almost deterministic moves and outcomes).

(a) DQN

• Q-network : \(Q_{\theta}(s, a)\)
• Target Q-Network : \(Q_{\theta^{-}}(s, a)\)

(b)Double Q-Learning

• 서로 다른 두 개의 Q-estimator를 가짐

(a) + (b) DDQN :

• key idea : “Target Network를 \(\max _{a \prime} Q\left(s^{\prime}, a^{\prime}\right)\) 계산위해 사용”

• Q-learning target : \(y=r+\gamma \max _{a \prime} Q_{\theta^{-}}\left(s^{\prime}, a^{\prime}\right)\).

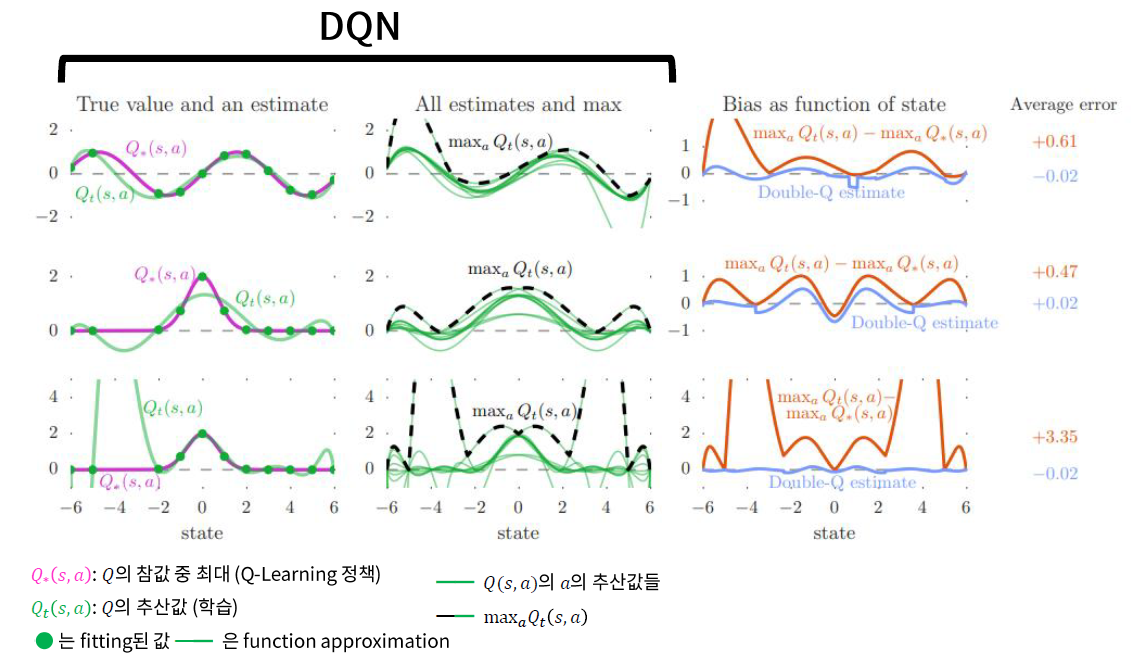
Result ( Maximization Bias 줄어든 효과 검증 )

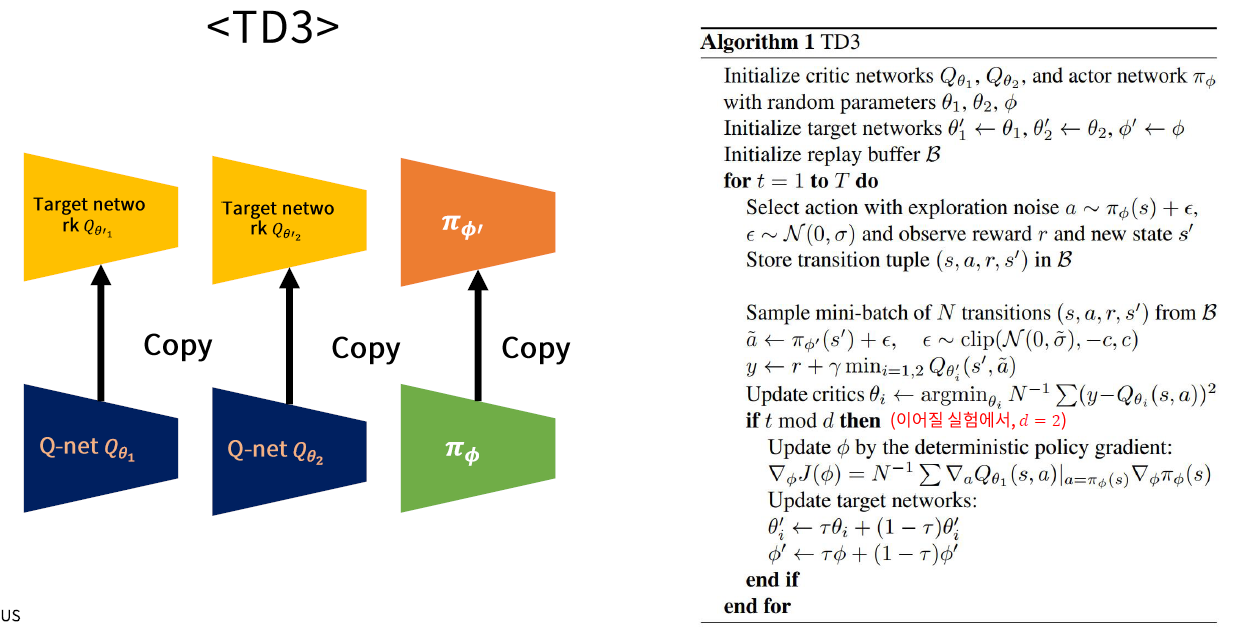
4. (Actor Critic) TD3

TD3 = DDPG + \(\alpha\)

Summary

• 1) (구) Double Q-Learning > (신) DDQN ( = Double Q-Learning + DQN )
• 2) SARSA style
• 3) # of Critic 업데이트 » # of Actor 업데이트
  • Policy Evaluation x 여러번
  • Policy Improvement x 1번

Problems of Actor-Critic method

( Actor Critic : 서로 다른 두 개의 NN이 interact하면서 학습됨. GAN의 학습이 어려운 이유도 마찬가지 )

Critic이 얼마나 잘 추산하느냐에 따라 Actor도 영향을 받게 됨.

• 문제 1) Over-estimation bias
• 문제 2) High variance of value-function estimation

\(\rightarrow\) TD3는 위 두 문제를 해결한다

(1) 문제 1 : Over-estimation bias

Problem

• Q-Learning에 비해, Actor-Critic에서는 이 문제가 덜 알려져 있다

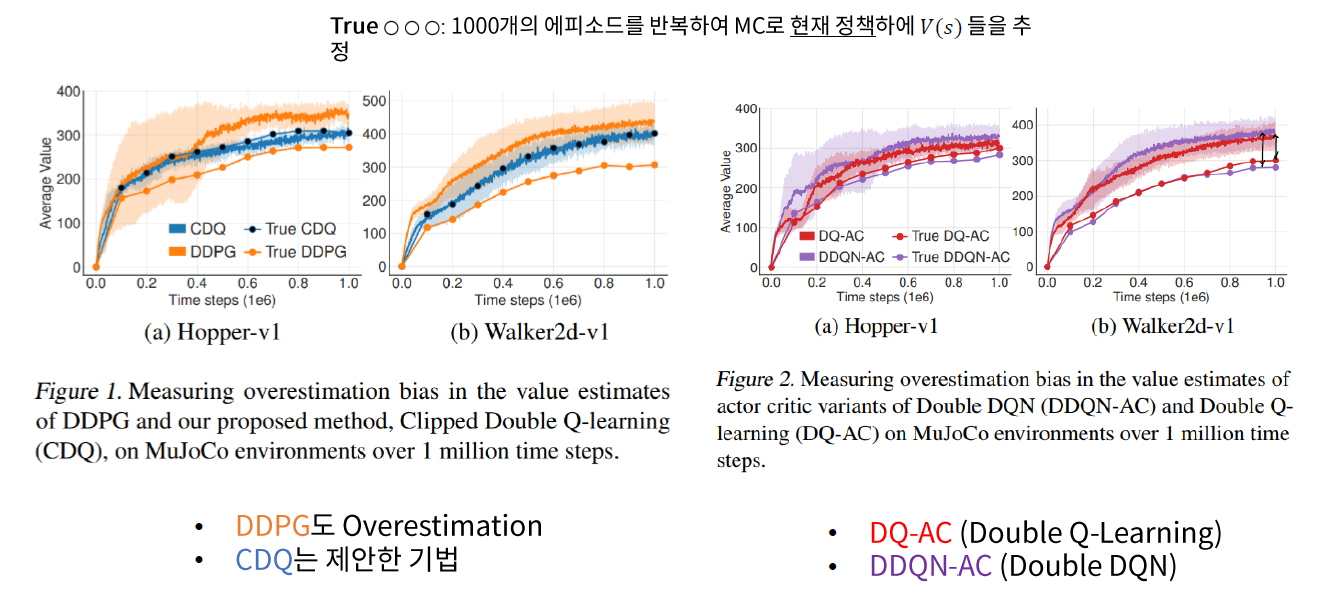
Solution

(A) (기존) DDQN (Double DQN)

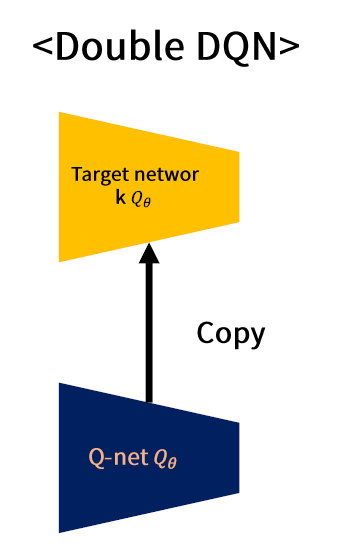
• Target Network \(\approx\) Main Network
• 둘이 너무 비슷해서, Double Q-estimator를 사용하는 효과 \(\downarrow\)

(B) (제안) CDQ (Clipped Double Q-Learning)

• 완전히 분리되어 있는 2개의 Network

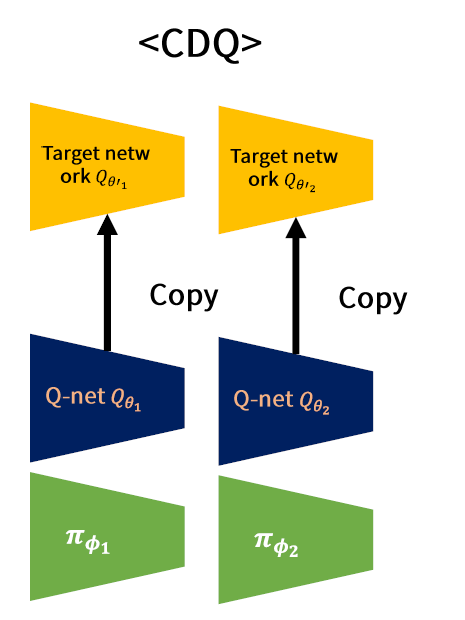
\(\begin{aligned} &y_{1}=r+\gamma \min _{i=1,2} Q_{\theta_{i}^{\prime}}\left(s^{\prime}, \pi_{\phi_{1}}\left(s^{\prime}\right)\right) \\ &y_{2}=r+\gamma \min _{i=1,2} Q_{\theta_{i}^{\prime}}\left(s^{\prime}, \pi_{\phi_{2}}\left(s^{\prime}\right)\right) \end{aligned}\) + DDPG 업데이트

• Train해야할 network가 총 4개

  ( 실제로는 3개의 network ( \(\pi\) 는 1개만 골라서 ) 학습한다 )

(2) 문제 2 : High variance of value-function estimation

Function Approximation에서 분산이 높아질 수 밖에 없는 이유?

\(\rightarrow\) Accumulating Error

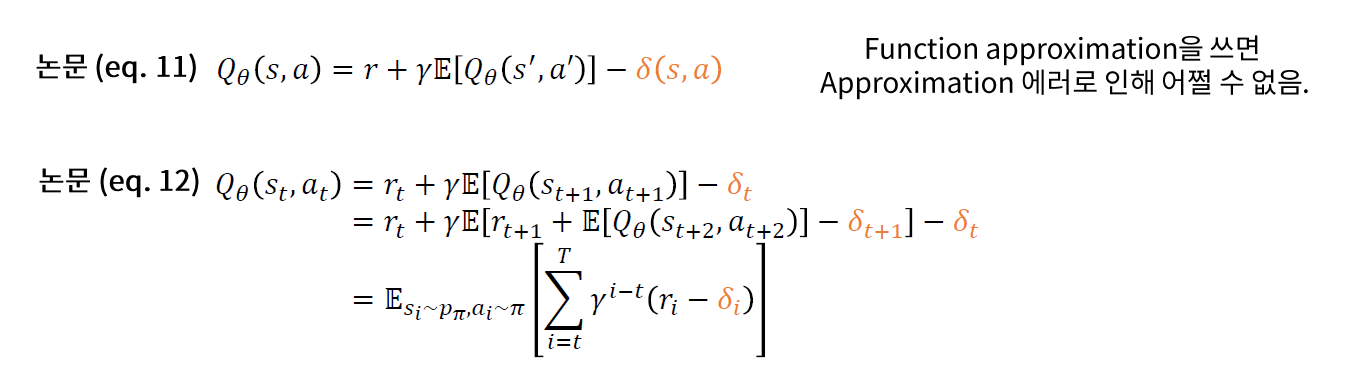
Solution

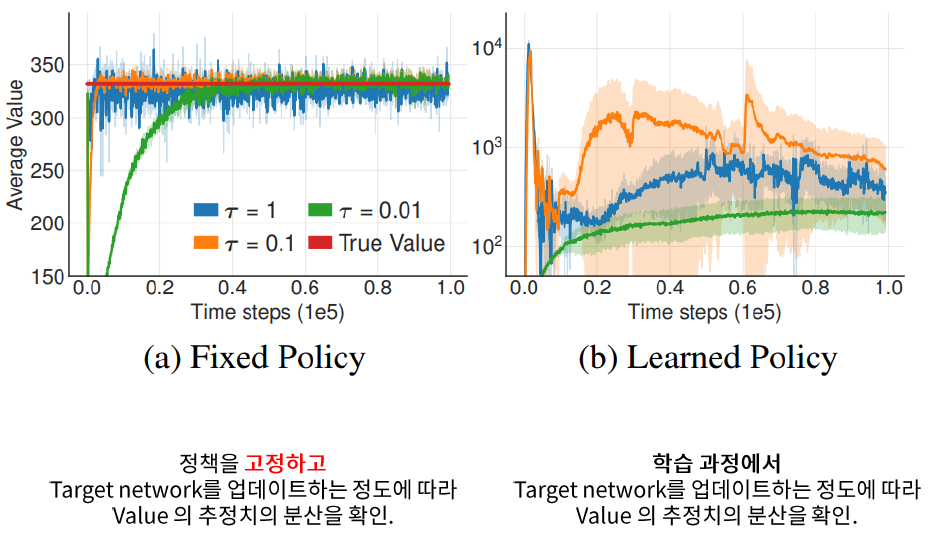
• target Network 사용 시, update 주기 \(\uparrow\)
• soft-update 시, \(\tau\) 를 더 줄여!

Experiment

• \(\tau\) 낮추니, 분산이 줄어듬! ( 수렴 속도는 약간 느려지지만 )
• 대신 더 많은 update수가 필요함

Target Policy Smoothing Regularization

\(y_{i}=r+\min _{i=1,2} \mathbb{E}_{\epsilon}\left[Q_{\theta_{i}^{\prime}}\left(s^{\prime}, \pi_{\phi}\left(s^{\prime}\right)+\epsilon\right)\right]\).

• \(\epsilon:\)noise ( ex. Gaussian noise )
• 같은 \(s\) 에서 ,비슷한 \(a\) 끼리 비슷한 \(Q(s, a)\) 를 가지게 유도

\(\mathbb{E}_{\epsilon}\left[Q_{\theta_{i}^{\prime}}\left(s^{\prime}, \pi_{\phi}\left(s^{\prime}\right)+\epsilon\right)\right]\) 계산 방법

• One-sample MC
• 저자 방식 ) \(y_{i}=r+\min _{i=1,2} Q_{\theta_{i}^{\prime}}\left(s^{\prime}, \pi_{\phi}\left(s^{\prime}\right)+\epsilon\right), \epsilon \sim \operatorname{clip}(\mathcal{N}(0, \sigma),-c, c)\)

(3) TD3 요약

위의 모든 techinque/algorithm들을 합친다

Key point

• 1) 2개의 독립된 Q function을 계산하는 NN을 만듬

  ( + 각각에 해당하는 Target Network도 ) ( + Actor Network는 1개만 사용 )

• [Replay Buffer]

  2) Action에 exploration noise ( with Gaussian )

  ( \(\leftrightarrow\) DDPG : OU process )

• [Training 시]

  3) Target Smoothing Noise

  ( Gaussian noise + clipping 해서 더함 )

  \(y_{i}=r+\min _{i=1,2} Q_{\theta_{i}^{\prime}}\left(s^{\prime}, \pi_{\phi}\left(s^{\prime}\right)+\epsilon\right), \epsilon \sim \operatorname{clip}(\mathcal{N}(0, \sigma),-c, c)\).

• 4) Soft-update