( 참고 : Fastcampus 강의 )
[ 44. 이산화된 공간에서 Planning ]
Contents
- Random Shooting
- MCTS (Monte-carlo Tree Search)
1. Random Shooting
SIMPLE!
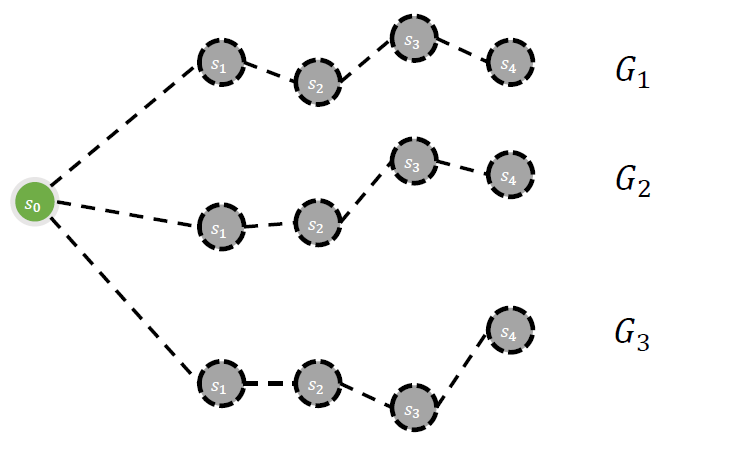
현재 state에서, random한 정책으로 여러 path (trajectory)를 생성한다.
그 중, 가장 좋은 trajectory를 선택한다!
2. MCTS (Monte-carlo Tree Search)
(1) 4개의 과정 소개
-
Tree traversal
-
Leaf node를 결정하는 과정
( = 바로 다음 state를 어디로 정할까? )
-
ex) UCB1
-
-
Node Expansion
- 탐색 tree에 새로운 node를 추가하는 과정
-
Roll Out :
- Simulation을 통해 미래 결과를 확인
-
Back-propgation
- Simulationn 결과를 (역순으로) tree에 반영
(2) UCB1
\(\operatorname{UCB} 1\left(s_{i}\right)=\bar{v}_{i}+2 \sqrt{\ln N / n_{i}}\).
- \(\bar{v}_{i}\) : \(s_i\)의 기대 가치
- \(N\) : 부모 node 방문 횟수
- \(n_i\) : \(s_i\) node 방문 횟수
(3) Example
(Step 1) 처음에는 두 node의 UCB1이 모두 \(\infty\)
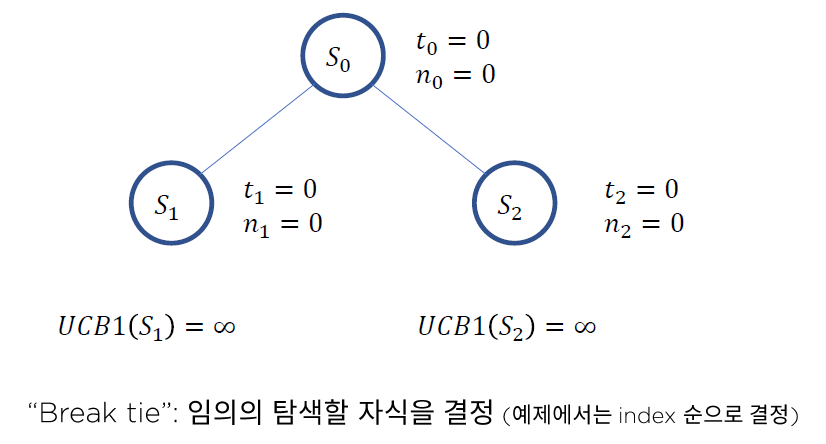
(Step 2) 그냥 index 순대로 \(S_1\) 선택
Question)
- Q1. Leaf node인가요? ( = 최하단 node인가요? )
- NO : keep going ( 더 내려가 )
- YES : Q2. 해당 Leaf node에 방문한 적있나요?
- NO : Roll-out ( Simulation 통해 가치 추산해보기 )
- YES : Node Expansion
- Roll-out을 통해, \(v=20\)임을 확인함
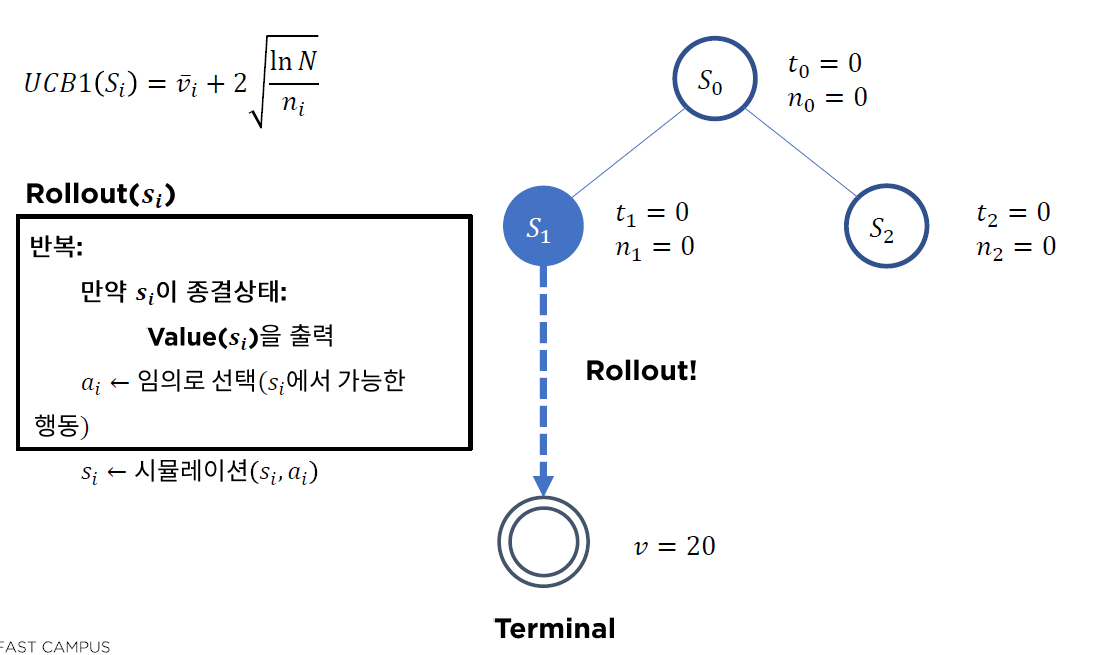
(Step 3) Back-propagation
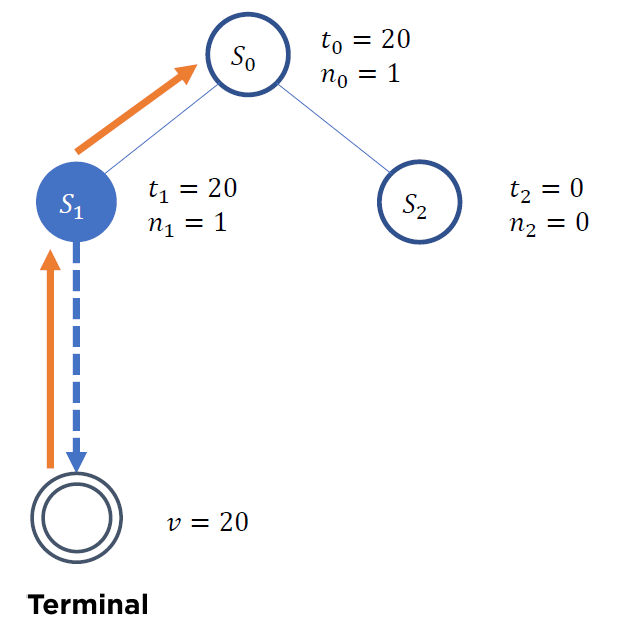
(Step 4) 위 과정 반복하여 \(S_2\)도 가치 추산
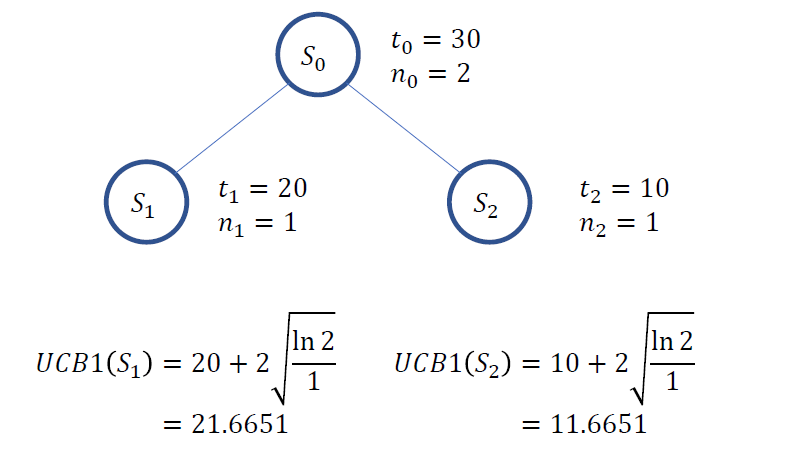
- 위의 결과, UCB1이 더 큰 \(S_1\) 이 선택됨
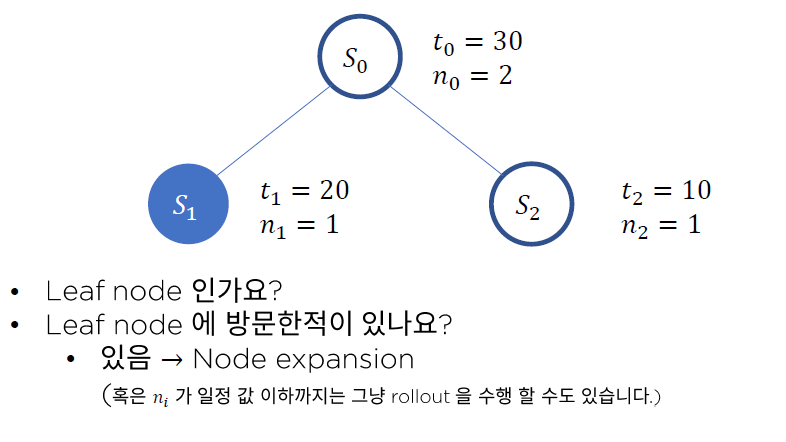
(Step 5) \(S_1\)에 node expansion
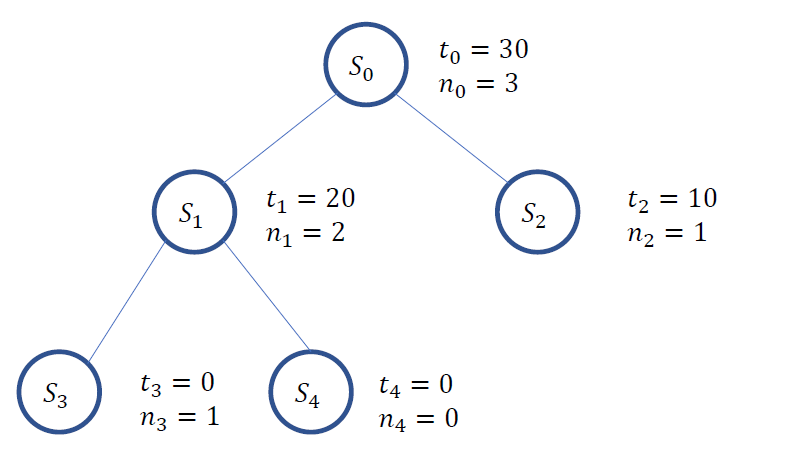
(Step 6) (과정 반복 통해 ) tree 완성 & 최적 행동 고르기
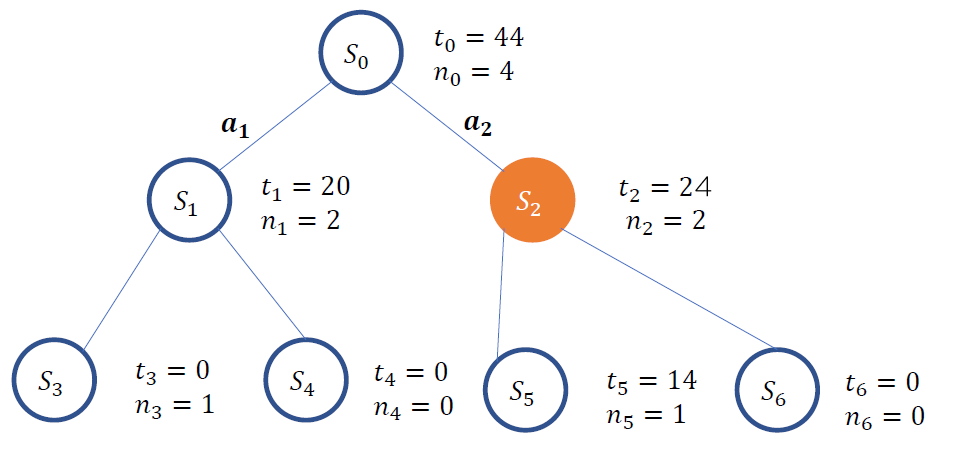
3. 바둑 as Markov Game
(1) Introduction
바둑은, 1명이 아닌 2명이 참여하는 게임이므로, 기존의 MDP로 모델링 할 수 없다.
Markov Game : \(<\mathcal{N}, \mathcal{S}, \mathcal{A}, P, R, \gamma>\)
마르코브 게임 \((M G)\) 는 \(\langle\mathcal{N}, \mathcal{S}, \mathcal{A}, P, R, \gamma>\) 인 튜플이다.
- \(\mathcal{N}\) : 의사 결정자의 집합
- \(n\) : 의사결정자의 수
- \(\delta\) : state의 집합
- \(\mathcal{A}\) : action의 집합
- n명의 의사 결정자가 있으므로, \(A: A_{1} \times A_{2} \ldots \times A_{n} \in \mathcal{A}\)
- \(P\) : transition model
- \(P: \mathcal{S} \times \mathcal{A} \rightarrow \mathcal{S}\).
- \(R\) : Return (보상 함수)
- n명의 의사 결정자가 있으므로, \(R: \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}^{n}\)
- \(\gamma\) : discount rate
- \(\gamma \in[0,1]\).
바둑 게임의 가정 : Two player zero-sum game
- \(n=2\), \(r^1 = -r^2\)
(2) 상대방 고르기
Not Too Easy, Not Too Hard!
-
Too Easy \(\rightarrow\) 너무 쉽게 이겨서, \(\pi_1\)이 그닥 좋지 못함
-
Too Hard \(\rightarrow\) 이겨본 적이 거의 없어서, \(\pi_1\)를 제대로 학습 못시킴
“학습 중인 자기 자신”을 상대방으로 삼아보자!
