01.Introduction to Recommender System

[ Recommender System ]

1. Introduction to Recommender System

( 참고 : Fastcampus 추천시스템 강의 )

1. Recommender System

• 구성요소 : (1) User & (2) Item
• Goal
  • 특정 User에게 “적합한 Item” 추천해주기
  • 해당 Item을 좋아할 “적합한 User” 추천해주기

2. User & Item

• User의 정보 : 사용자 고유의 정보(나이, 성별 등) & 사용자의 로그 (접속 시간, 주요 접속 시간 대)
• Item의 정보 : 아이템의 고유 정보 (가격, 출시년도, 종류 등)

3. 추천 점수

• 직관적 이해 : User & Item 간의 matching 점수
• 좋은 추천 알고리즘 = 추천 점수를 잘 점수화(Scoring)하는 알고리즘

4. 추천 시스템이 푸는 문제

• 랭킹 문제

  • User가 특정 Item을 “좋아할지 안할지” ( 정확한 점수 파악은 X )

  • User가 좋아할 Item TOP 5

    Item을 좋아할 User TOP 5

• 예측 문제

  • User가 특정 Item을 “얼마나 좋아할지” ( = score )
  • User x Item Matrix를 채워나가야
    • 채워져 있는 값 : for model training
    • 비워져 있는 값 : for model testing

5. 추천 알고리즘의 종류

1. Contents-based Rec Sys (컨텐츠 기반) :

   • 사용자의 과거 소비 Item 분석을 통해, 해당 아이템과 비슷한 Item 추천

     ( ex. A맛의 와인을 좋아함 \(\rightarrow\) A맛과 비슷한 와인 추천 )

   • Cold start 문제 해결에 도움

2. Collaborative-Filtering (협업 필터링) :

   • 비슷한 성향을 가진 유저가 좋아하는 아이템을 해당 유저에게 추천

     ( ex. A와 B는 소비패턴이 99% 비슷한 사람 \(\rightarrow\) A가 산 물건을 B에게도 추천 )

   • 새로운 Item에 대한 추천 부족

3. Hybrid Rec Sys (하이브리드) :

   • Contents-based Rec Sys + Collaborative-Filtering ( 장.단 보완 )

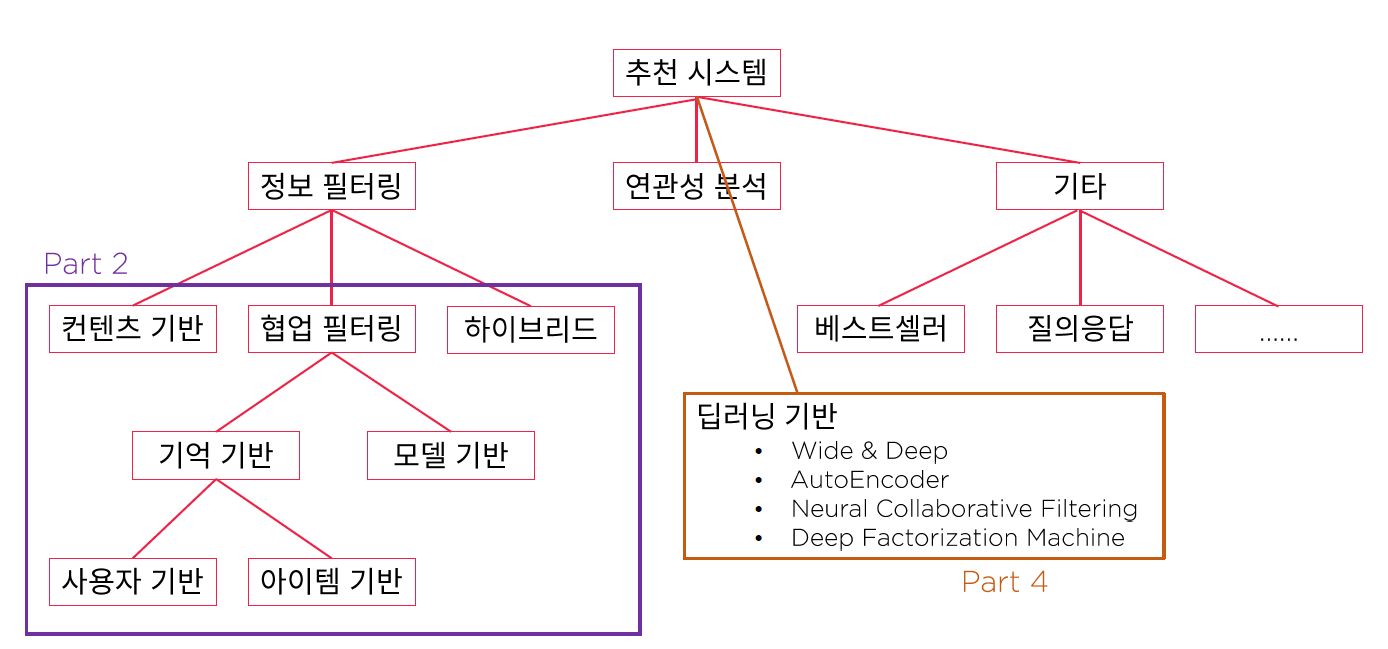
( 출처 : Fast campus )

6. 추천 시스템의 한계

• Scalability ( 실제 데이터는, 학습/분석에 사용한 데이터보다 다양하고 많다 )
• Proactive Rec Sys ( 이론에서 배우는 것은, 유저의 행동/정보 제공 이후에 추천을 해주지만, 실제로는 특별한 요청 없이 사전에 먼저 제공해야 경쟁력 있는 서비스 )
• Cold-Start

7. 추천 시스템 평가

• RMSE (Root Mean Square Error)
  • \[\mathrm{RMSE}=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}.\]
• NDCG (Normalized Discounted Cumulative Gain)
  • Top N의 리스트 내에, 관심있어하는 Item이 포함되는지에 따라
  • 순위에 따라 다른 weight 부여 가능
  • ( cumulative 비교 ) 정답 ranking vs 모델 ranking
  • 1에 가까울 수록 Good & Log Normalization에 따른 순위에 따른 가중치 부여
  • (아래 참고)
• 기타 ( Precision, Mean Average Precision, Precison, Recall, AUC … )

More about NDCG

( rel : 관련 있는 정도(relevant)…binary 혹은 complex value 로 표현 가능 )

1) CG ( Cumulative Gain )

• 상위 item p개의 gain ( p개 간에는 동일한 weight )
• \[C G_{p}=\sum_{i=1}^{p} r e l_{i}.\]

2) DCG ( Discounted Cumulative Gain )

• CG와 마찬가지로 상위 item p개의 gain이나, 갈수록 낮아지는 weight

  ( = 높은 순위의 값을 더 정확히 맞히는 것이 중요 = 하위권에 penalty 부여 )

• \[D C G_{p}=r e l_{1}+\sum_{i=2}^{p} \frac{r e l_{i}}{\log _{2} i}.\]

3) NDCG ( Normalized Discounted Cumulative Gain )

• IDCG (Ideal DCG, 이상적인 DCG) = 전체 p개의 결과가 가질 수 있는 조합 중 최대값

• \(N D C G_{p}=\frac{D C G_{p}}{I D C G_{p}}\).

8. Similarity의 종류

1. Euclidean Distance :

   \[\begin{array}{l} \sqrt{\left(a_{1}-b_{1}\right)^{2}+\left(a_{2}-b_{2}\right)^{2}+\cdots+\left(a_{n}-b_{n}\right)^{2}}= \sqrt{\sum_{i=1}^{n}\left(a_{i}-b_{i}\right)^{2}} \end{array}.\]

2. Cosine Similarity :

   \(a \cdot b=\|a\|\|b\| \cos \theta\).

   \(\text { similarity }=\cos (\theta)=\frac{A \cdot B}{\|A\|\|B\|}=\frac{\sum_{i=1}^{n} A_{i} \times B_{i}}{\sqrt{\sum_{i=1}^{n}\left(A_{i}\right)^{2}} \times \sqrt{\sum_{i=1}^{n}\left(B_{i}\right)^{2}}}\).

3. Jaccard Similarity :

   ( 집합의 개념 사용! 공통 Item이 없으면 0, 모두 겹치면 1 )

   \(J(A, B)=\frac{\mid A \cap B\mid}{\mid A \cup B\mid}=\frac{\mid A \cap B\mid}{\mid A\mid +\mid B\mid-\mid A \cap B\mid}\).

4. Pearson Correlation (Similarity) :

   \(r_{x y}=\frac{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum_{i}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum_{i}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}}\).