[ Recommender System ]
11. Factorization Machine
( 참고 : Fastcampus 추천시스템 강의 , https://seunghan96.github.io/ml/stat/Factorization_Machine/ )
paper : Factorization Machines ( Rendle, 2010 ) (https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5694074)
1. Abstract
Factorization Machine = SVM + Factorization model
- ex) Matrix Factorization, Parallel FA, specialized model ( SVD++, PITF, FPMC, … )
“General predictor”
- classification, regression 둘 다 OK
linear time complexity
2. Introduction
-
High sparsity에서도 reliable parameter 예측 가능
( \(\leftrightarrow\) SVM은 sparse한 데이터에 부적합 )
-
complex interaction도 잡아냄
-
factorized parameterization
-
linear time complexity
Contribution
- 1) Sparse Data에서도 OK
- 2) linear time complexity
- 3) General predictor
3. Prediction under sparsity
MF vs FM
-
Matrix Factorization : user / movie / rating 만을 사용
-
Factorization Machine : 위의 정보 외에도, 추가적인 정보 활용 가능
ex) D년도에 A친구가 B영화를 보고 준 평점 C점
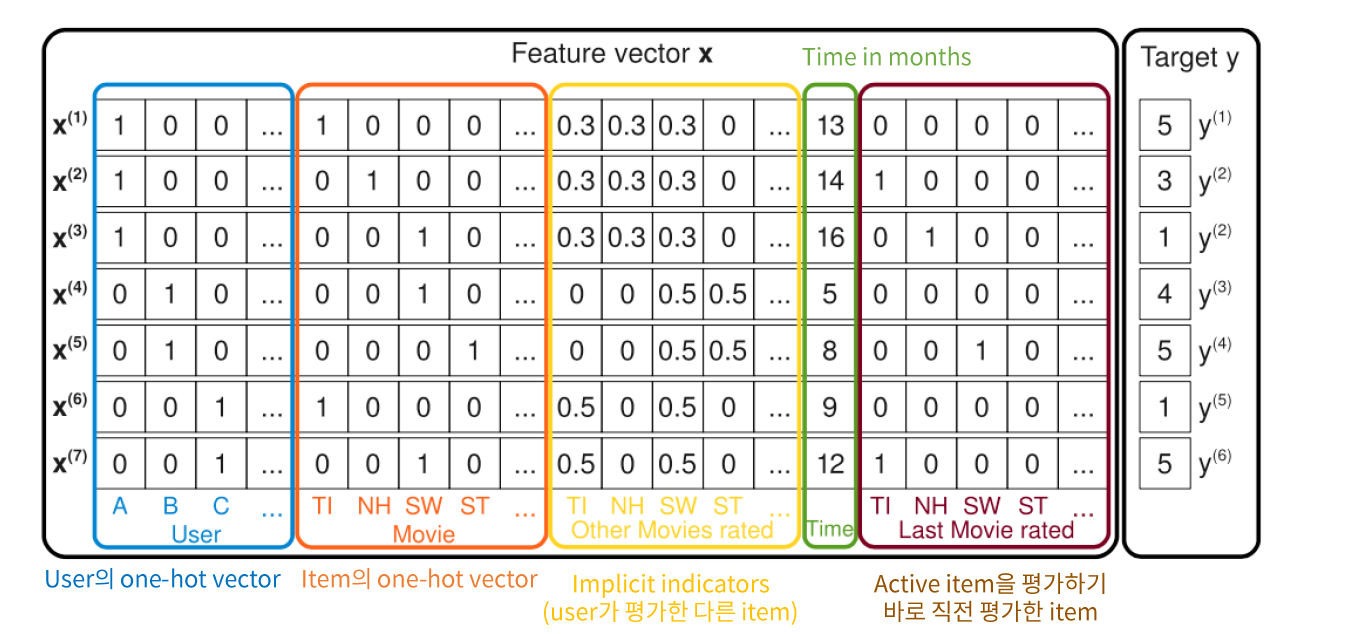
Feature vector \(x\)는, 위와 같이 유저/아이템 외에도 다양한 정보들을 담을 수 있다.
( one-hot vector로 인해 sparse하긴 하지만, 그럼에도 불구하고 잘 작동하게 된다 )
4. Factorization Machine
Model equation : \(\hat{y}(\mathbf{x}):=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle x_{i} x_{j}\).
- 2-way FM : 개별 변수 / 두 변수 간의 interaction을 capture한다
- (Multiple Regression의) coefficient가 Embedding vector의 내적인 꼴!
-
Matrix Factorization : \(\mathbf{W}_u \times \mathbf{W}_i\)
( user & item의 latent vector)
-
Factorization Machine : \(\mathbf{W}_i \times x_i\)
( 이제 user & item말고도 더 다양한 \(x\)들이 구성 된다. 이것들 마다의 latent vector를 구한다! )
\(\sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle x_{i} x_{j}\).
-
모든 변수 간의 latent vector 조합을 생성
-
time complexity : \(O(kn^2) \rightarrow O(kn)\)
\(\begin{aligned}{c} &\sum_{i=1}^{n} \sum_{j=i+1}^{n}<v_{i}, v_{j}>x_{i} x_{j} \\&=\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n}<v_{i}, v_{j}>x_{i} x_{j}-\frac{1}{2} \sum_{i=1}^{n}<v_{i}, v_{i}>x_{i} x_{i} \\ &=\frac{1}{2}\left(\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{f=1}^{k} v_{i, f}, v_{j, f} x_{i} x_{j}-\sum_{i=1}^{n} \sum_{f=1}^{k} v_{i, f} v_{i, f} x_{i} x_{i}\right) \\ &=\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)\left(\sum_{j=1}^{n} v_{j, f} x_{j}\right)-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right) \\ &=\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right) \end{aligned}\).
5. Factorization Machine as predictors
1) Regression ( LSE 사용 )
2) Binary classification ( 0,1 예측 )
3) Ranking ( set 점수 as Order )
6. Learning FM
GD(Gradient Descent)를 사용해서 update된다.
각각의 parameter에 대한 gradient는 다음과 같다.
\(\frac{\partial}{\partial \theta} \hat{y}(\mathbf{x})=\left\{\begin{array}{ll} 1, & \text { if } \theta \text { is } w_{0} \\ x_{i}, & \text { if } \theta \text { is } w_{i} \\ x_{i} \sum_{j=1}^{n} v_{j, f} x_{j}-v_{i, f} x_{i}^{2}, & \text { if } \theta \text { is } v_{i, f} \end{array}\right.\).
7. d-way Factorization Machine
위의 2-way를 d-way로 generalize한 모델이다.
\(\begin{array}{l} \hat{y}(x):=w_{0}+\sum_{i=1}^{n} w_{i} x_{i} +\sum_{l=2}^{d} \sum_{i_{1}=1}^{n} \ldots \sum_{i_{l}=i_{l-1}+1}^{n}\left(\prod_{j=1}^{l} x_{i_{j}}\right)\left(\sum_{f=1}^{k_{l}} \prod_{j=1}^{l} v_{i_{j}, f}^{(l)}\right) \end{array}\).
8. Conclusion
-
factorized interaction을 사용하여 feacture vector \(x\)의 모든 가능한 interaction을 capture
-
high sparsity에서도 잘 작동함
( unobserved interaction에 대해서도 일반화 )
-
Linear time complexity
-
Optimize using SGD
-
기존의 모델들 (SVM, MF 등)보다 뛰어난 performance
