[ Recommender System ]
12. Wide and Deep Learning for Recommender System
( 참고 : Fastcampus 추천시스템 강의 )
paper : Wide and Deep Learning for Recommender System ( HT Cheng et al., 2016 )
( https://arxiv.org/abs/1606.07792 )
[ Abstract ]
WIDE : 주어진 데이터를 “외운다” ( memorization )
-
cross-product feature transformation
( feature간의 interaction 고려 )
-
(단점..?) more feature engineering effort!
DEEP : 일반화 ( generalization )
-
to unseen feature combination
( 보지 못한 새로운 조합에 대한 예측 성능 \(\uparrow\) )
-
less feature engineering effort
-
over-generalize
WIDE와 DEEP 둘을 조합하여 좋은 장점을 취한 모델!
1. Introduction
Memorization의 정의
-
Frequent co-occurence of items & features
-
exploit correlation (of historical data)
\(\rightarrow\) more topical & directly relevant to the items
Generalization의 정의
-
explore new feature combination
\(\rightarrow\) improve diveristy!
< 기존 모델의 한계 >
- **1) GLM **
- ( ex. Logistic Regression )
- 다양한 feature를 생성하여 학습해야
- “Memorization”에 focus \(\rightarrow\) overfitting
- 2) Embedding based Model
- ( ex. FM, DNN )
- “Generalization”에 focus \(\rightarrow\) 섬세한 추천 불가
Contributions
- (1) Wide & Deep Learning Framework 제안 ( NN + LM )
- (2) Google Play store에 적용 + test
- (3) 오픈 소스로 제공
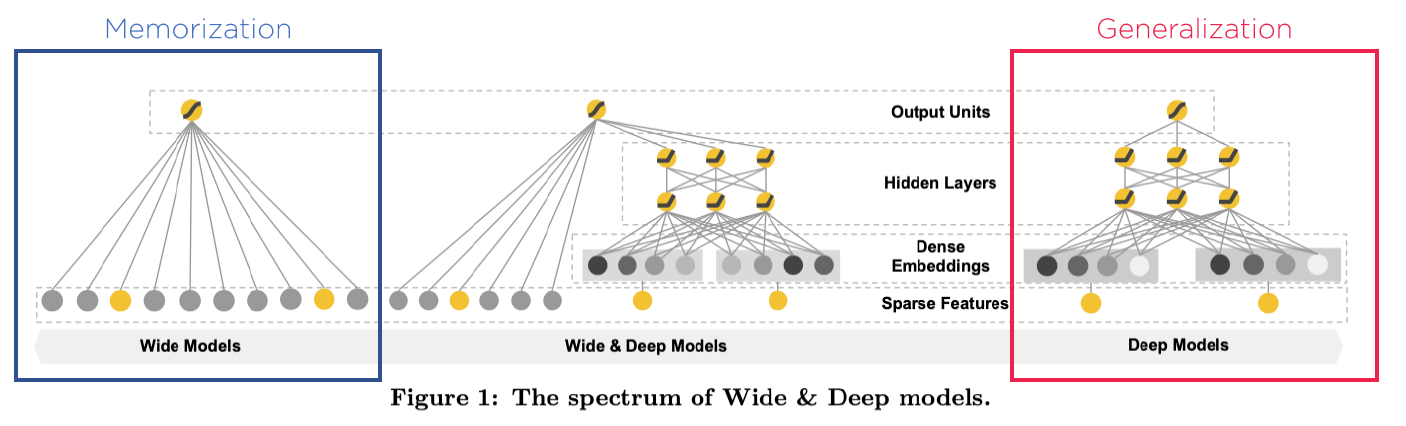
2. Recommender System Overview
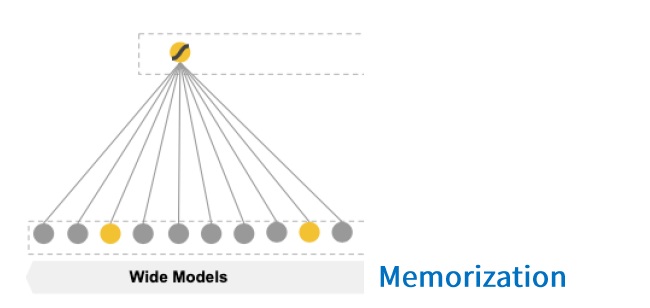
3-1. The WIDE Component
GLM : \(y = w^Tx+b\)
-
\[x = [x_1,..,x_d]\]
( 구성 : raw input feature + cross-product feature )
- \(y\) : 유저의 행동 여부
Cross-product feature

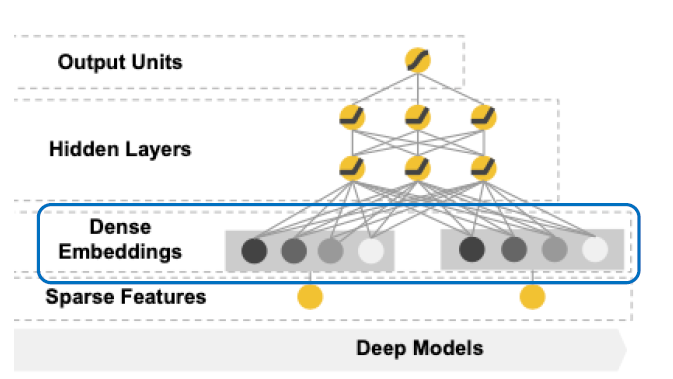
3-2. The DEEP Component
Embedding using NN : \(a^{l+1}=f(W^{(1)}a^{(1)}+b^{(1)})\)
3-2 Joint Training of Wide & Deep Model
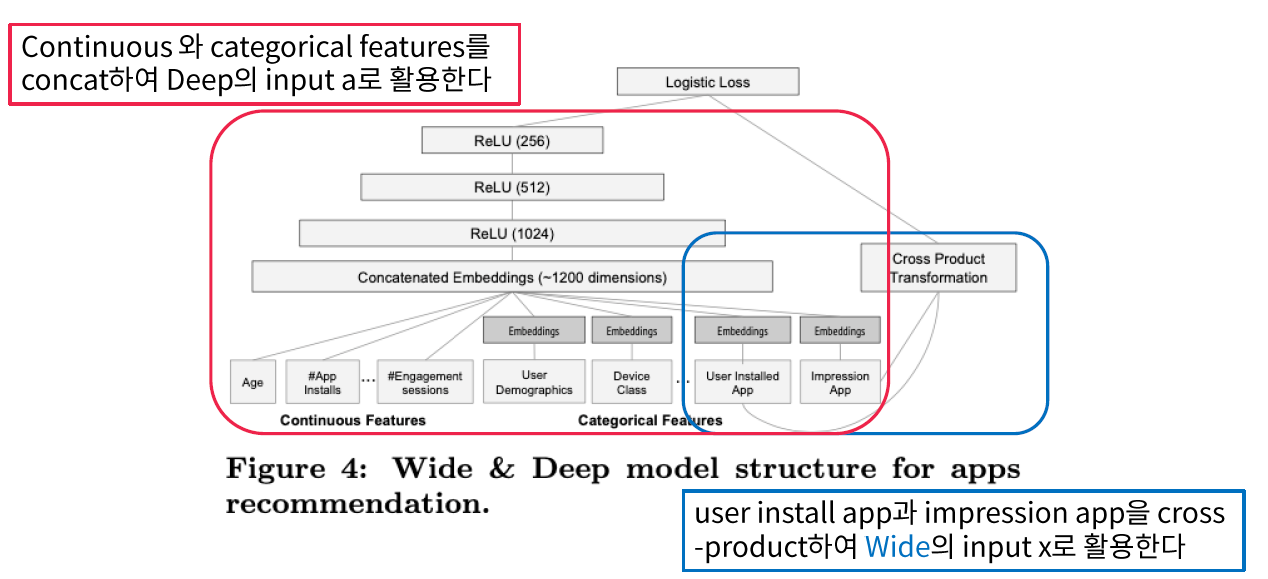
최종적인 output : \(P(Y=1 \mid X)\)
- app을 다운받을 확류
- \(P(Y=1 \mid \mathbf{x})=\sigma\left(\mathbf{w}_{w i d e}^{T}[\mathbf{x}, \phi(\mathbf{x})]+\mathbf{w}_{d e e p}^{T} a^{\left(l_{f}\right)}+b\right)\).
Backpropagation은 wide & deep part 모두에게 동시에 이루어진다.
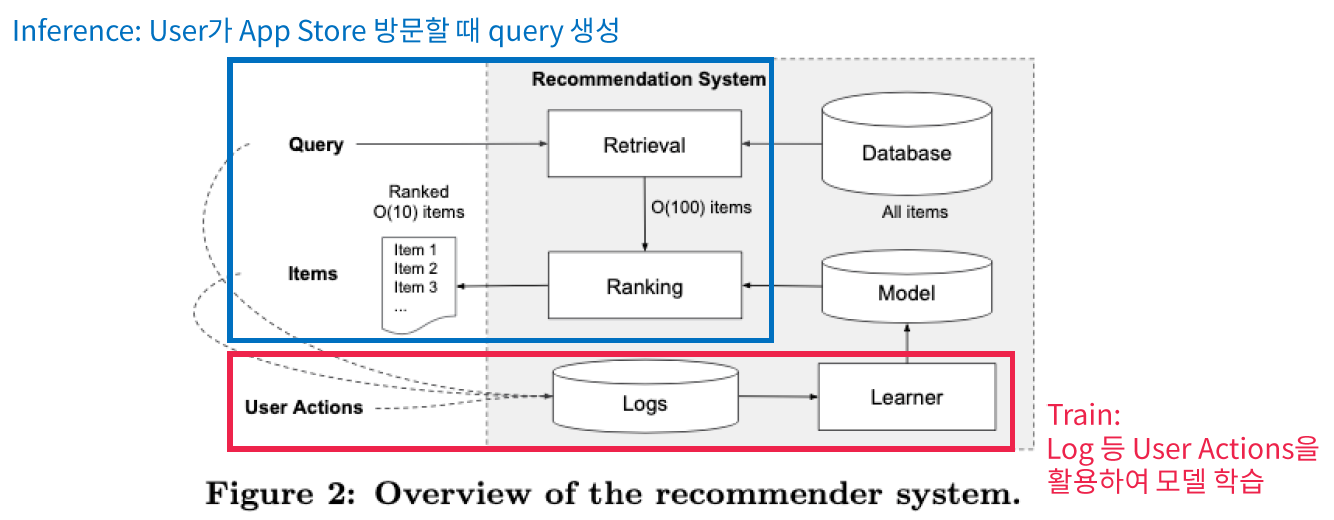
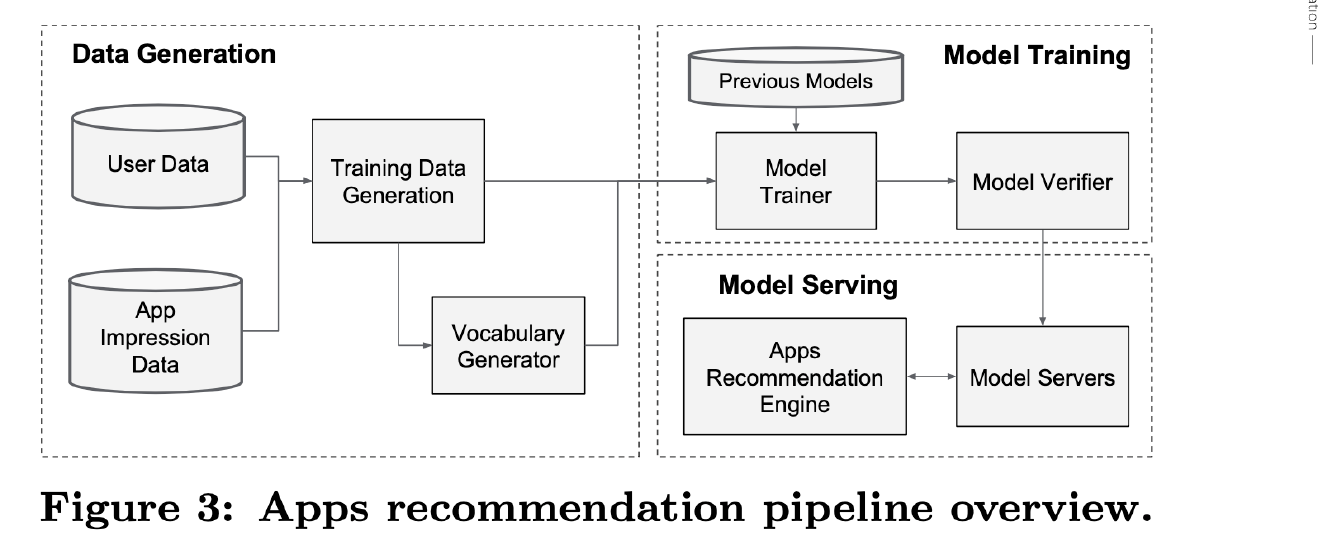
4. System Implementation
Pipeline은 아래와 같다.
5. Conclusion
- Wide ( for Memorization ) + Deep ( Generalization )
- GLM + Embedding NN
