[ Recommender System ]
14. DeepFM : A Factorization-Machine based Neural Network for CTR prediction
( 참고 : Fastcampus 추천시스템 강의 )
paper : DeepFM : A Factorization-Machine based Neural Network for CT prediction ( Guo et al., 2017 )
( https://arxiv.org/pdf/1703.04247.pdf )
[ Abstract ]
DeepFM
- Wide&Deep + Factorization Machine
-
goal : Predict CTR ( Click Through Rate )
-
low & high-order interaction 모두 학습
-
Raw feature그대로 사용 ( feature engineering 노력 $\downarrow$ )
( 이전의 Deep&Wide에는 cross-product 생성 등의 feature engineering 과정이 필요했었다 )
1. Introduction
-
CTR : Click Through Rate ( = 추천한 항목을 click 할까? )
-
Learn Implicit Feature interaction ( explicit은 당연히 O )
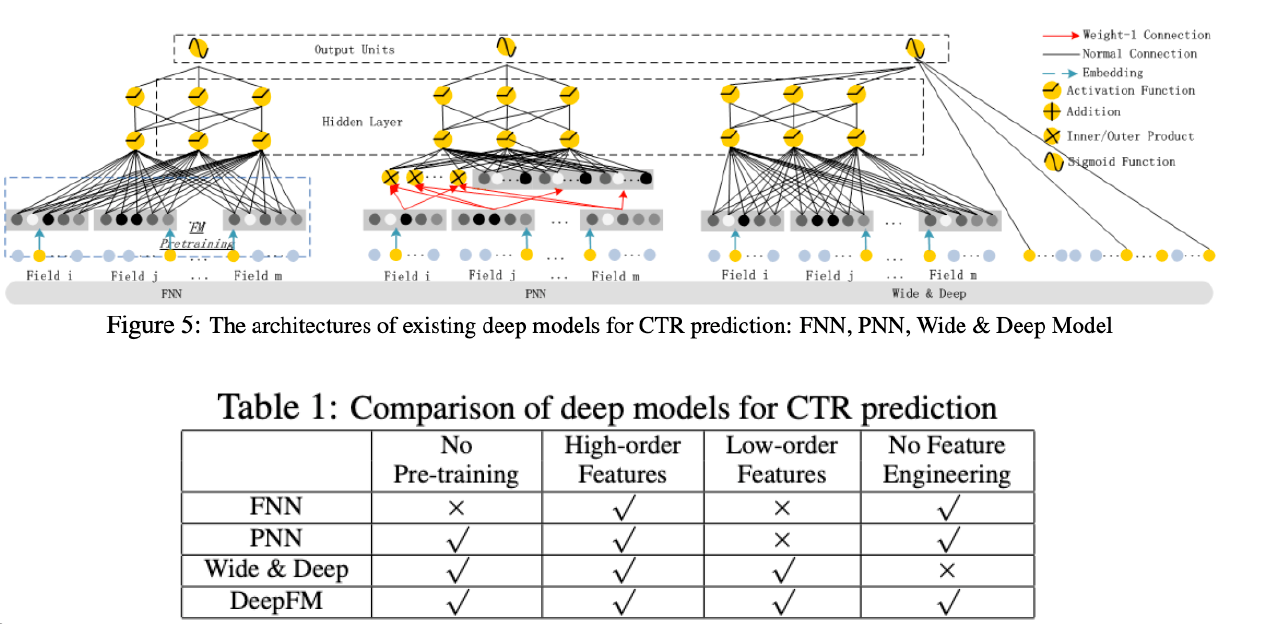
Previous works
- GLM
- high-order feature interaction 잡기 어려움
- FM
- high-order feature interaction 잡지만, complexity cost 높음
- CNN & RNN for CTR Prediction
- CNN-based는 주변 feature에 집중
- RNN-based는 sequential
- FNN (Factorization-machine supported NN)
- NN 사용을 통한 high-order 포착 쉬움 but low-order는 그닥
- pre-trained FM 성능에 의존
- Wide & Deep
- low & high-order 잘 잡아내지만, wide component에서 feature engineering 필요
Contribution
-
1) Propose DeepFM
- Deep : high-order
- FM : low-order
- End-to-End 학습 가능
-
2) Efficient training
( $\because$ input & embedding vector를 share )
-
3) CTR prediction에서 높은 성능을 보임
2. Deep FM
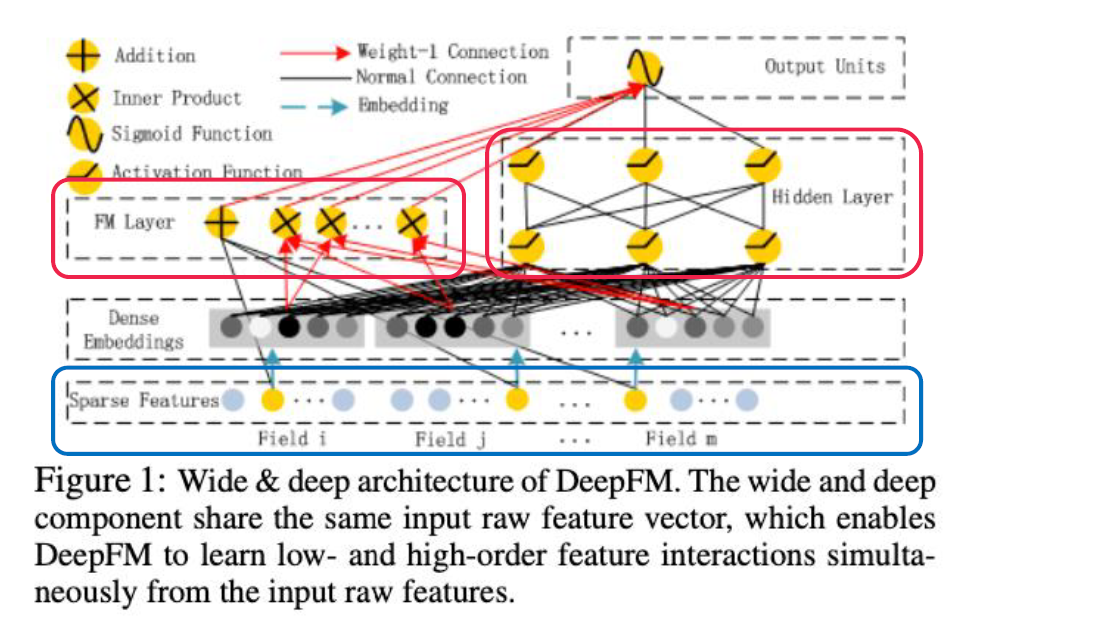
-
Left ) Wide component
Right ) Deep component
$\rightarrow$ 이 둘은 같은 input raw feature vector를 사용함
Sparse Feature & Dense Embeddings
-
$x=\left[x_{\text {field }{1}}, x{\text {field }{2}}, \ldots, x{\text {field }_{m}}\right]$
-
노란색 부분 : embedding vector $ (x_{\text{field}_i}w_i = V_i)$
-
feature $i$
-
$w_{i}$: order-1 importance
-
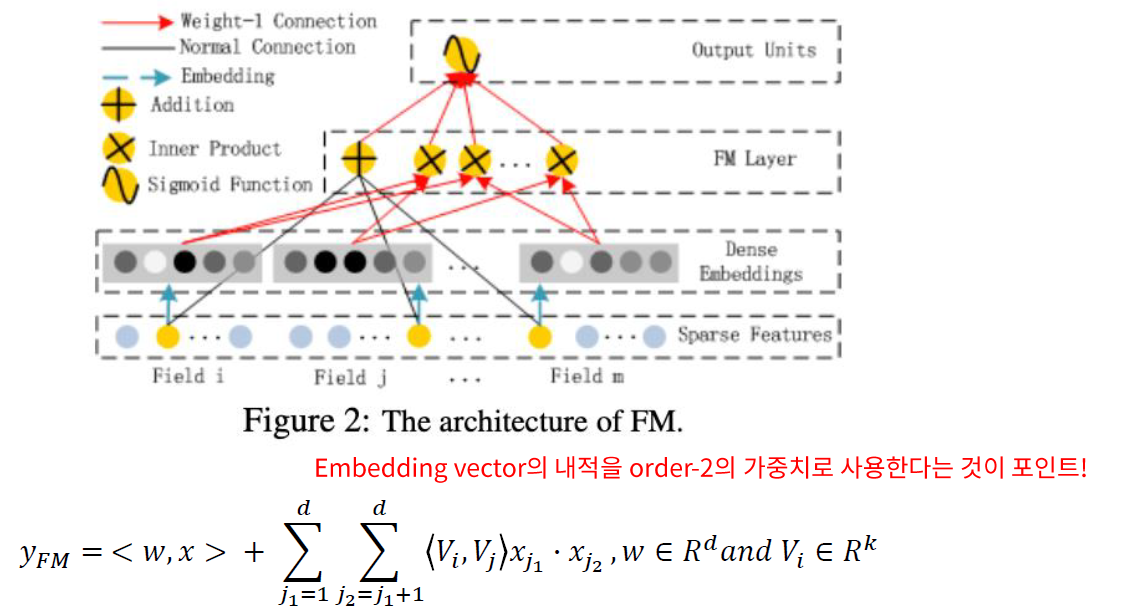
$V_i$ : latent vector ( used to measure its impact of interactions with other features )
( fed into FK component to model order-2 feature interaction )
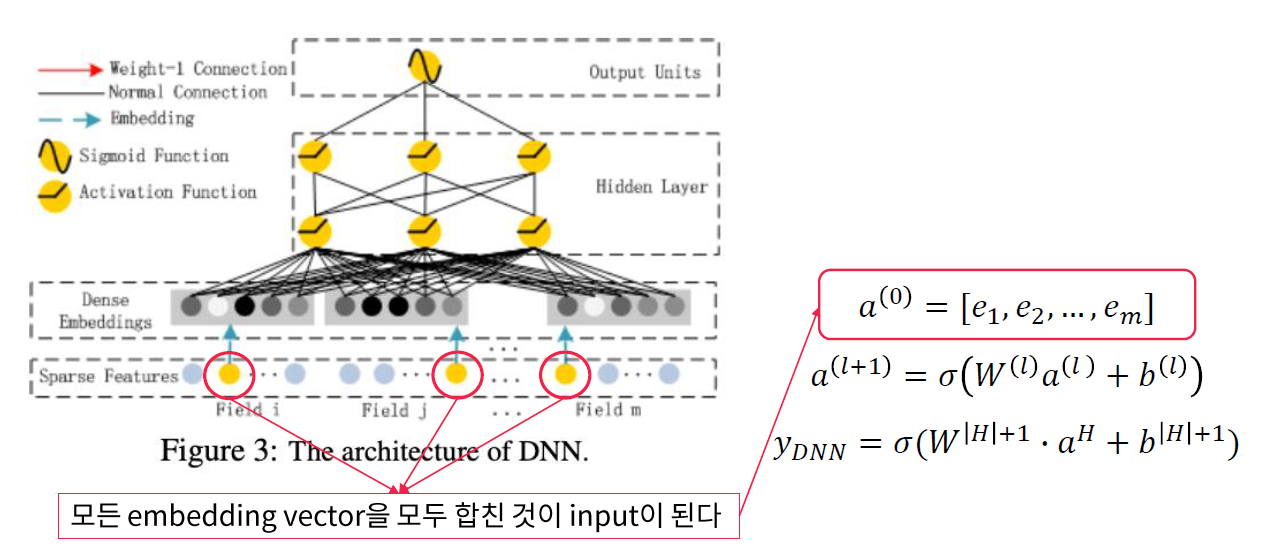
( fed into deep component to model high-order feature interaction )
-
Output
- $\hat{y}=\operatorname{CTR}_{-} \operatorname{model}(x)$, $ \hat{y} \in(0,1)$
- $\hat{y}=\operatorname{sigmoid}\left(y_{F M}+y_{D N N}\right)$
(1) FM component
(2) Deep Component
Relationship with other NN
3. Conclusion
-
Deep + FM component
( input & embedding vector를 share )
-
Pre-training 필요 X
-
High & Low order feature interaction 둘 다 모델링
