[ Recommender System ]
9. Neural Collaborative Filtering
( 참고 : Fastcampus 추천시스템 강의 )
paper : Neural Collaborative Filtering ( He, et al., 2017 ) (https://arxiv.org/abs/1708.05031)
1. Abstract
-
기존의 Matrix Factorization에 한계 O ( linear한 관계밖에 잡아내지 X )
-
NN기반의 CF으로 non-linearity를 capture
-
보다 Complex한 user & item한 관계를 captuer
Contributions
- 1) General Framework NCF = user & item의 latent factor을 모델링하는데에 NN사용
- 2) Matrix Factorization = NCF의 special case
- 3) 여러 Experiment를 통해 효과 입증
2. Learning from Implicit Data
( Implicit Data = “함축적”인 데이터 ( 유저가 직접적으로 제공한 데이터가 X ) )
interaction(관측)이 있는지의 여부 ( \(\neq\) 선호 여부 )
Let \(M\) and \(N\) denote the number of users and items, respectively.
We define the user-item interaction matrix \(\mathbf{Y} \in \mathbb{R}^{M \times N}\) from users’ implicit feedback as \(y_{u i}=\left\{\begin{array}{ll}1, & \text { if interaction (user } u, \text { item } i \text { ) is observed; } \\ 0, & \text { otherwise. }\end{array}\right.\)
- interaction function \(f\) : user & item간의 interaction의 여부를 예측 ( probability )
- 2 objective function
- (1) point-wise loss : 실제값 - 예측값 ( as regression )
- (2) pair-wise loss : 1이 0보다 크도록 margin 최대화
3. Matrix Factorization
User-interaction matrix의 한계점

- low dimension representation으로 인한 complex 관계 포착 X
- if large dimension ? overfitting
\(\rightarrow\) NON-linearity를 부여! with Neural Network
4. NCF (Neural Collaborative Filtering)
NCF의 구조는 아래와 같이 간단하다.
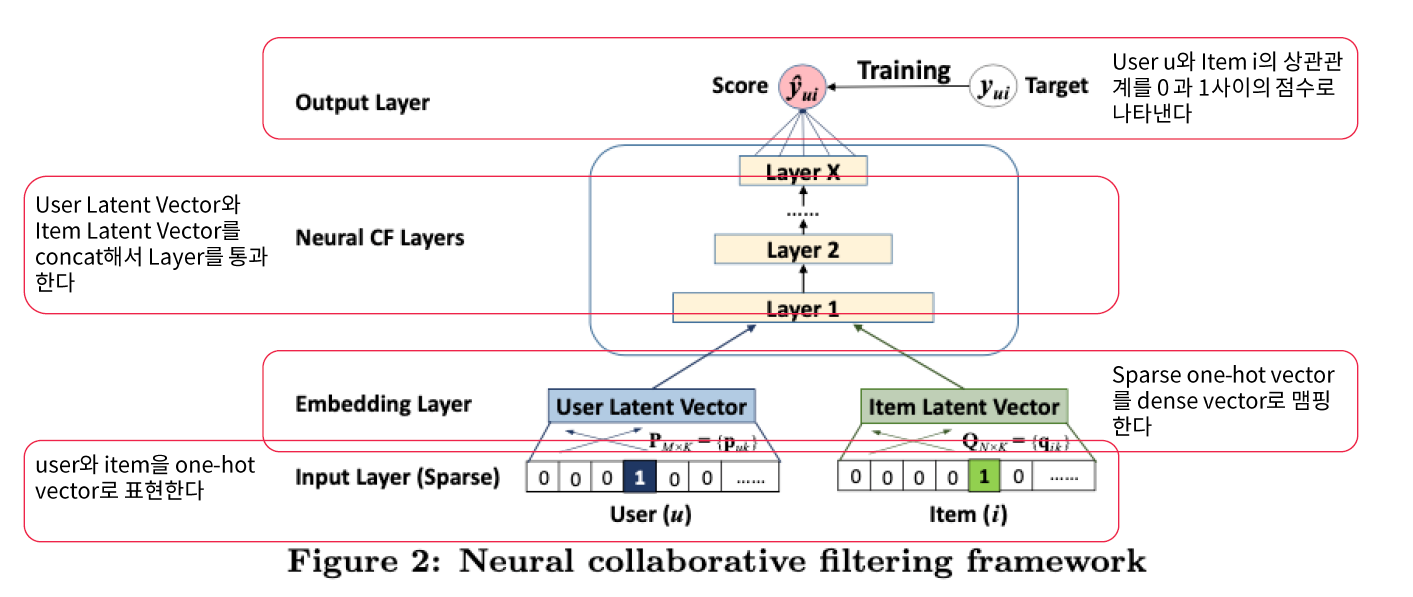
(1) output : Bernoulli distn ( \(\because\) binary output )
(2) loss function : Binary cross-entropy (NLL)
-
\(p\left(\mathcal{Y}, \mathcal{Y}^{-} \mid \mathbf{P}, \mathbf{Q}, \Theta_{f}\right)=\prod_{(u, i) \in \mathcal{Y}} \hat{y}_{u i} \prod_{(u, j) \in \mathcal{Y}^{-}}\left(1-\hat{y}_{u j}\right)\).
-
( in log form )
\[\begin{aligned} L &=-\sum_{(u, i) \in \mathcal{Y}} \log \hat{y}_{u i}-\sum_{(u, j) \in \mathcal{Y}^{-}} \log \left(1-\hat{y}_{u j}\right) \\ &=-\sum_{(u, i) \in \mathcal{Y} \cup \mathcal{Y}^{-}} y_{u i} \log \hat{y}_{u i}+\left(1-y_{u i}\right) \log \left(1-\hat{y}_{u i}\right) \end{aligned}\]
(3) optimizer : SGD
(1) GMF (Generalized Matrix Factorization)
MF는 NCF의 special case!
- let \(\phi_{1}\left(p_{u}, q_{i}\right)=p_{u} \odot q_{i}\)
- \(p_u\) : user의 latent vector
- \(q_i\) : item의 latent vector
- then, \(\widehat{y_{u i}}=a_{\text {out }}\left(h^{T}\left(p_{u} \odot q_{i}\right)\right)\).
- 여기서 \(a=1\)이고, \(h\)가 uniform vector라면 이것이 곧 Matrix Factorization이다!
(2) MLP (Multi-Layer Perceptron)
GMF보다 간단하게 학습 가능
\(\begin{aligned} \mathbf{z}_{1} &=\phi_{1}\left(\mathbf{p}_{u}, \mathbf{q}_{i}\right)=\left[\begin{array}{c} \mathbf{p}_{u} \\ \mathbf{q}_{i} \end{array}\right] \\ \phi_{2}\left(\mathbf{z}_{1}\right) &=a_{2}\left(\mathbf{W}_{2}^{T} \mathbf{z}_{1}+\mathbf{b}_{2}\right) \\ & \ldots \ldots \\ \phi_{L}\left(\mathbf{z}_{L-1}\right) &=a_{L}\left(\mathbf{W}_{L}^{T} \mathbf{z}_{L-1}+\mathbf{b}_{L}\right) \\ \hat{y}_{u i} &=\sigma\left(\mathbf{h}^{T} \phi_{L}\left(\mathbf{z}_{L-1}\right)\right) \end{aligned}\).
(3) Fusion of GMF & MLP
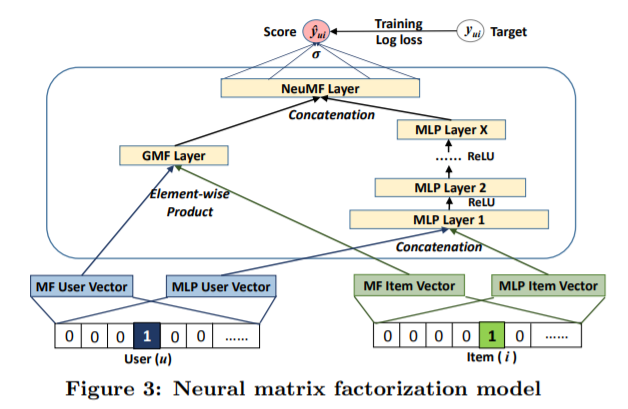
\(\begin{aligned} \phi^{G M F} &=\mathbf{p}_{u}^{G} \odot \mathbf{q}_{i}^{G} \\ \phi^{M L P} &=a_{L}\left(\mathbf{W}_{L}^{T}\left(a_{L-1}\left(\ldots a_{2}\left(\mathbf{W}_{2}^{T}\left[\begin{array}{c} \mathbf{p}_{u}^{M} \\ \mathbf{q}_{i}^{M} \end{array}\right]+\mathbf{b}_{2}\right) \ldots\right)\right)+\mathbf{b}_{L}\right) \\ \hat{y}_{u i} &=\sigma\left(\mathbf{h}^{T}\left[\begin{array}{l} \phi^{G M F} \\ \phi^{M L P} \end{array}\right]\right. \end{aligned}\).
GMF & MLP의 latent dimension은 다를 수 있음
최종 output : GMF & MLP의 output을 concatenate한 뒤 산출
- GMF : linearity
- MLP : non-linearity
\(\rightarrow\) 이 둘을 (모두 혹은 하나만) 사용해서 output 생성 가능!
5. Conclusion
- General Framework NCF를 제안 ( GMF, MLP, NeuralMF )
- NN을 사용하여 non-linearity capture
- GMF + MLP = Neural MF \(\rightarrow\) 성능 향상
- base : Collaborative Filtering ( = User & Item 간의 Interaction에 focus )
