ReMixMatch : Semi-Supervised Learning with Distribution Alignment and Augmentation Anchoring (2020)
Contents
- Abstract
- ReMixMatch
- Distribution Alignment
- Improved Consistency Regularization
0. Abstract
Improve MixMatch, using 2 new techniques :
- (1) distribution alignment
- (2) augmentation anchoring
(1) Distribution alignment
-
encourages the marginal distn of predictions on unlabeled data,
to be close to the marginal distn of groundtruth labels
(2) Augmentation anchoring
- feeds multiple strongly augmented versions of an input into the model
- encourages each output to be close to the prediction for a weakly-augmented version
1. ReMixMatch
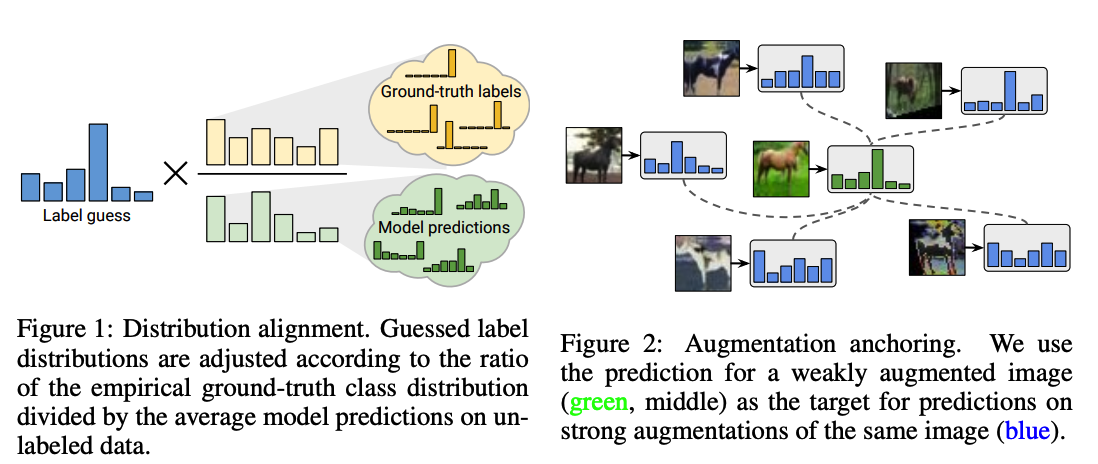
(1) Distribution Alignment
enforces that the aggregate of predictions on unlabeled data matches the distn of the provided labeled data
a) Input-Output Mutual Information
Maximize mutual info between model’s input & output for labeled data
\[\begin{aligned} \mathcal{I}(y ; x) &=\iint p(y, x) \log \frac{p(y, x)}{p(y) p(x)} \mathrm{d} y \mathrm{~d} x \\ &=\mathcal{H}\left(\mathbb{E}_x\left[p_{\text {model }}(y \mid x ; \theta)\right]\right)-\mathbb{E}_x\left[\mathcal{H}\left(p_{\text {model }}(y \mid x ; \theta)\right)\right] \end{aligned}\]- (1) 1st term :
- not widely used in SSL
- encourages that the model predicts each class with equal frequency
- (2) 2nd term :
- familiar entropy minimization objective
- encourage each individual model output to have low entropy
b) Distn Alignment in ReMixMatch (fig 1)
MixMatch
- already includes entropy minimization via sharpening
Therefore, intereseted in incorporating a form of “fairness”
- \(\mathcal{H}\left(\mathbb{E}_x\left[p_{\text {model }}(y \mid x ; \theta)\right]\right)\) : not useful, when \(p(y)\) is not uniform!!
\(\rightarrow\) Thus, use distribution alignment
Distribution Alignment :
- \(\tilde{p}(y)\) : running average of model’s predictions on unlabeled data
- given model prediction \(q=p_{\text {model }}(y \mid u ; \theta)\),
- (1) scale \(q\) by \(p(y)/ \tilde{p}(y)\)
- (2) then renormalize
(2) Improved Consistency Regularization
a) Augmentation Anchoring (fig 2)
Why is MixMatch with AutoAugment unstable ?
\(\rightarrow\) it averages the prediction across \(K\) augmentations
( Strong augmentation : can result in disparate predictions … so no meaning in average! )
Proposal :
- step 1) generate an “anchor” by applying weak augmentation to unlabeled data
- step 2) generate \(K\) strongly-augmented version of the same unlabeled data
- using CTAugment (Control Theory Augment)
- step 3) use the guessed label as the target for all of the \(K\) images
b) Control Theory Augment
- pass
