9.(EM algorithm) Latent Variable Models

1. Latent Variable Models

(1) Latent Variable Models

A latent variable model is a model that relates observable variables to latent variables. So, what is latent variable?

(wikipedia) Latent variables (as opposed to observable variables) are variables that are not directly observed but are rather inferred (through a mathematical model) from other variables that are observed (directly measured)

For example, your company is trying to recruit a person. And there are many things to consider for who to choose. There may be variables such as ‘age’,’GPA’,’IQ score’, etc… Those are all ‘observable variables’, which you can score in numerically. With those variables, you make a new variable “Intelligence”, which is a not diretcly observable variable. This “Intelligence” is a ‘latent variable’. And latent variable models are models that use such variables.

So, what is good about latent variable models?
They are simple models, with fewer parameters. Also, latent variables are sometimes meaningful. Look at the example above. We can say the new latent variable ‘Intelligence” as the meaningful factor when considering who to choose as a new employee.

(2) Probabilistic Clustering

Clustering is an unsupervised ML, which groups similar data into the same group. There are two big types of clustering, which are “hard” clustering and “soft” clustering.

Hard clustering assigns each data into only one cluster. On the other hand, soft clustering assigns each data several clusters with a different weight. It assign each data point a ‘probability distribution’ over clusters. For example, if there are three clusters A,B,C, one data point x_1 can belong to 0.6A + 0.2B + 0.2*C.

https://image.slidesharecdn.com/textclustering-150803041805-lva1-app6891/95

These are the main two reasons why we want to cluster data in a soft way

[1] better in tuning hyper parameter
The good thing about clustering in probabilistic way is that it is much more better in tuning hyper parameters. Let’s take an example of ‘the number of clusters’. In GMM(Gaussian Mixture Model), which is one way of soft clustering, the log likelihood of training dataset will be higher(get better) if the number of cluster increases. But it doesn’t mean that it is always good to have a larger number of clusters, since the validation dataset will show a decrease in the log likelihood after a certain point. But in the case of hard clustering(ex. K-means), no matter of the training dataset and the validation dataset, larger number of cluster always shows a smaller loss, which makes us hard to decide how many clusters to make.

[2] generating new data points
We may want to build a generative model of our data. If we treat everything probabilistically, we may sample new data from our model. For example, in the case of face image, sampling new images from the same probability distributions means that we can generate fake face from scratch.

(3) GMM (Gaussian Mixture Model)

How can we model our data probabilistically? One good way is using GMM, a Gaussian Mixture Model.
Gaussian mixture model is a probabilistic model that assumes all the data points are generated from a mixture of a finite number of Gaussian distributions with unknown parameters. (scikit-learn).


https://miro.medium.com/max/753/1*lTv7e4Cdlp738X_WFZyZHA.png

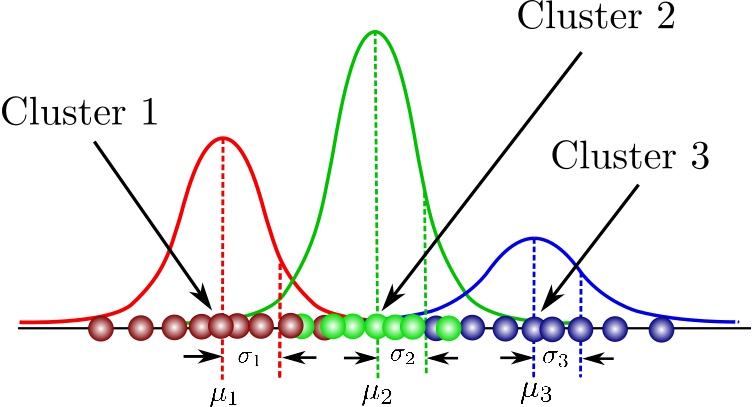
In this case, we assume that each data point come from one of the three Gaussians. Each Gaussians represents one cluster. It means that the more Guassians you use in the mixture, the more cluster you are using.
Let’s look at how one data point gets its cluster.
The density of each data points is the weighted sum of three Gaussian densities, like the expression below.



The parameter ‘theta’ here are



Compared to one Gaussian, GMM has more flexibility. But it has more parameters to decide.

The way to train GMM is to find the values of the parameters which maximizes the likelihood ( = density of data set, given the parameters).

which are subject to

How do we optimize this? We use ‘EM algorithm’, which we will talk about later. There are two reasons why we do not use SGD(Stochastic Gradient Descent) here, and use EM algorithm instead. First, it may be hard to follow the constraints, which is written above (like positive semi-definite covariance matrices). Second, EM algorithm is sometimes much more faster and efficient.

As a summary, GMM is a flexible probability distribution, which can be better trained with EM algorithm than SGD.

(4) Training GMM

It is easy to find the Gaussian distribution if we all know the sources of each data point. But in reality, we don’t know the sources. We need Gaussian parameters to estimate our sources. But also, to estimate the Gaussian parameters, we need the sources! We solve this problem with EM algorithm.

EM algorithm

• Step 1) Start with 2 randomly placed Gaussian parameters theta
• Step 2) Until convergence, repeat :
  a) For each point, compute p(t=c | x_i, theta) ( = does x_i look like it came from cluster c? )
  b) Update Gaussian parameters theta to fit points assigned to them
  The illustration below shows how the Gaussian parameters are updated after several iterations.
  
  https://i.stack.imgur.com/Z5mcu.png