Revisiting Deep Learning Models for Tabular Data

Revisiting Deep Learning Models for Tabular Data (NeurIPS 2021)

https://arxiv.org/pdf/2106.11959.pdf

Contents

1. Introduction
2. Related Work
3. Models for tabular data problems
   1. MLP
   2. ResNet
   3. FT-Transformer
4. Experiments
   1. Scope of the comparison
   2. Datasets
   3. Implementation details
   4. Comparing DL models
   5. DL vs. GBDT
5. Analysis
   1. FT-Transformer vs ResNet
   2. Ablation Study

Abstract

DL methods for Tabular Data

• not properly compared

  ( different benchmarks & experiment protocols )

This paper: perform an overview of the main families of DL archs

( + raise the bar of baselines in tagbular DL )

2 powerful simple architectures

• (1) ResNet
• (2) FT-Transformer

1. Introduction

Using DL for tabular data is appealing

\(\because\) allow constructing multi-modal pipelines

\(\rightarrow\) large number of DL methods were proposed, but lack of well-established benchmarks & datasets

( + unclear what DL model is SOTA )

2 architectures

• (1) ResNet
• (2) FT-Transformer

Findings

• (1) None of the previous DL methods consistently outperform ResNet!
• (2) (Proposed) FT-Transformer demonstrates the best performance on most tasks
• (3) NO UNIVERSAL SOTA in tabular domain

2. Related Work

(1) ML : shallow SOTA

GBDT, XGBoost, LightGBM, CatBoost

(2) DL

a) Differentiable Trees

• motivated by performance of decision tree ensembles

• DL + trees : end-to-end (X)

  \(\rightarrow\) solution : smooth decision functions

• still, do not consistently outperform ResNet!

b) Attention-based models

Findings: properly tuned ResNet outperforms existing attention-based methods

c) Explicit modeling of multiplicative interactions

several works criticize MLP

\(\because\) unsuitable for modeling multiplciative interactions between features

\(\rightarrow\) some works have proposed ifferent ways to incorporate feature products into MLP

Still … not superior to properly tuned baselines

3. Models for tabular data problems

Try to reuse well-established DL building blocks

• ResNet
• (propose) FT-Transformer

Notation

Dataset: \(D=\left\{\left(x_i, y_i\right)\right\}_{i=1}^n\)

• where \(x_i=\left(x_i^{(\text {num })}, x_i^{(\text {cat })}\right) \in \mathbb{X}\)
• total number of features = \(k\)

Data split : \(D=D_{\text {train }} \cup D_{\text {val }} \cup D_{\text {test }}\)

3 types of tasks:

• (1) binary classification \(\mathbb{Y}=\{0,1\}\)
• (2) multiclass classification \(\mathbb{Y}=\{1, \ldots, C\}\)
• (3) regression \(\mathbb{Y}=\mathbb{R}\).

(1) MLP

\(\operatorname{MLP}(x) =\operatorname{Linear}(\operatorname{MLPBlock}(\ldots(\operatorname{MLPBlock}(x))))\).

• \(\operatorname{MLPBlock}(x) =\operatorname{Dropout}(\operatorname{ReLU}(\operatorname{Linear}(x)))\).

(2) ResNet

\(\operatorname{ResNet}(x) =\operatorname{Prediction}(\operatorname{ResNetBlock}(\ldots(\operatorname{ResNetBlock}(\operatorname{Linear}(x)))))\).

• \(\operatorname{ResNetBlock}(x) =x+\operatorname{Dropout}(\operatorname{Linear}(\operatorname{Dropout}(\operatorname{ReLU}(\operatorname{Linear}(\operatorname{BatchNorm}(x))))))\).
• \(\operatorname{Prediction}(x) =\operatorname{Linear}(\operatorname{ReLU}(\operatorname{BatchNorm}(x)))\).

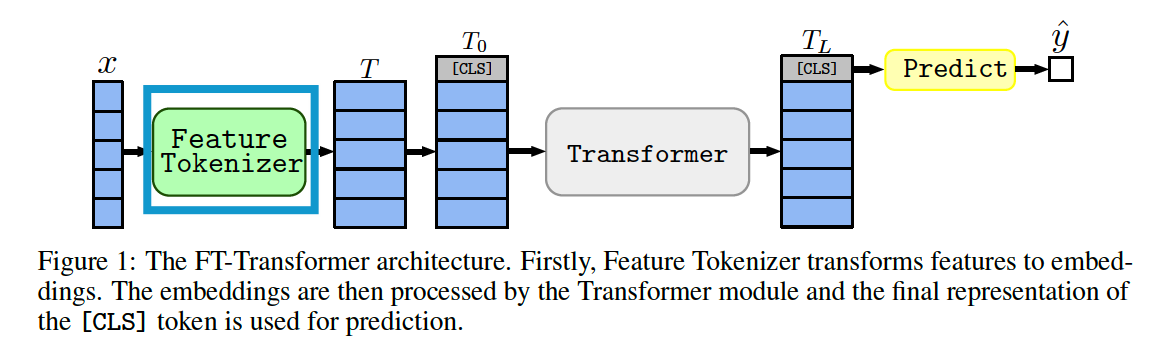
(3) FT-Transformer

FT = Feature Tokenizer

• transforms ALL features ( cat + num ) into embeddings
• every transformer layers operates on the feature level of one object

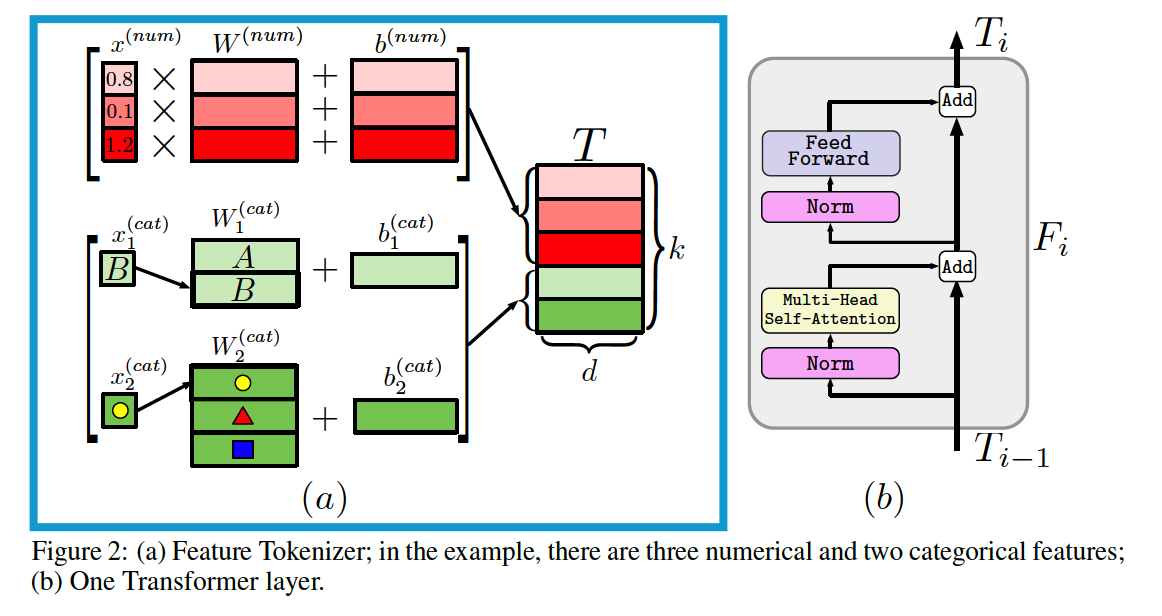
a) Feature Tokenizer

Input features : \(x\)

Output embeddings : \(T \in \mathbb{R}^{k \times d}\).

• \(T_j=b_j+f_j\left(x_j\right) \in \mathbb{R}^d \quad f_j: \mathbb{X}_j \rightarrow \mathbb{R}^d\).

\(\begin{array}{ll} T_j^{(\text {num })}=b_j^{(\text {num })}+x_j^{(\text {num })} \cdot W_j^{(\text {num })} & \in \mathbb{R}^d, \\ T_j^{(\text {cat })}=b_j^{(\text {cat })}+e_j^T W_j^{(\text {cat })} & \in \mathbb{R}^d, \\ T=\operatorname{stack}\left[T_1^{(\text {num })}, \ldots, T_{k^{(\text {num })}}^{(\text {num })}, T_1^{(\text {cat })}, \ldots, T_{k(\text { cat })}^{(\text {cat })}\right] & \in \mathbb{R}^{k \times d} . \end{array}\).

• \(W_j^{(\text {num })} \in \mathbb{R}^d\).

• \(W_j^{(\text {cat })} \in \mathbb{R}^{S_j \times d}\).

• \(e_j^T\) : one-hot vector for the corresponding categorical feature.

b) Transformer

embedding of the [CLS] token is appended to \(T\)

& \(L\) Transformer layers \(F_1, \ldots, F_L\) are applied:

• \(T_0=\operatorname{stack}[[\mathrm{CLS}], T] \quad T_i=F_i\left(T_{i-1}\right)\).

c) Prediction

• \(\hat{y}=\operatorname{Linear}\left(\operatorname{ReLU}\left(\operatorname{LayerNorm}\left(T_L^{[\text {CLS] }}\right)\right)\right)\).

d) Limitations

FT-Transformer : requires more resources ( compared to ResNet. )

Still, possible to distill FT-Transformer into simpler models

4. Experiments

(1) Scope of the comparison

Do not employ model-agnostic DL practices

• ex) pretraining, additional loss, data augmentatio …

\(\because\) goal is to evaluate the impact of inductive biases imposed by architectures

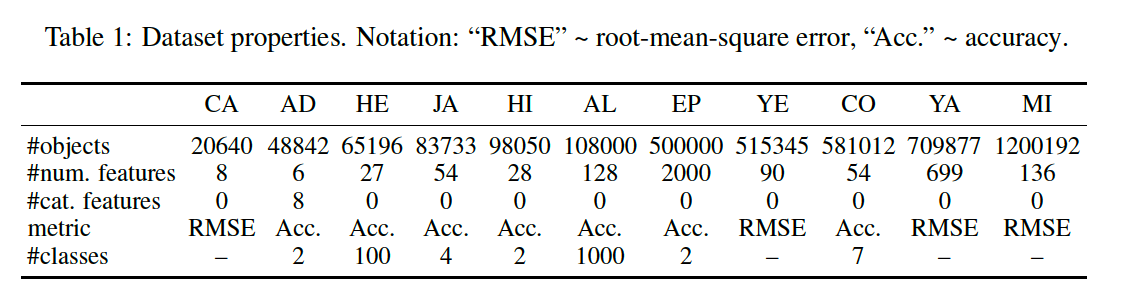
(2) Datasets

11 public datasets

(3) Implementation details

a) Data Preprocessing

( same prerpocessing for all deep models )

• quantile transformation
• Standardization ( to Helena & ALOI )
• Raw features ( to Epsilon )
• standardize to regression targets

b) Evaluation

15 exp with different random seeds

c) Ensembles

3 ensembles ( 5 models per each ) = total 15 models

(4) Comparing DL models

Main takeaways

• MLP: still a good sanity cehck

• ResNet : effective baseline

• FT-Transformer : best on most tasks

• Tunining makes simple models ( MLP, ResNet .. ) competitive!

  \(\rightarrow\) recommend tuning the baselines

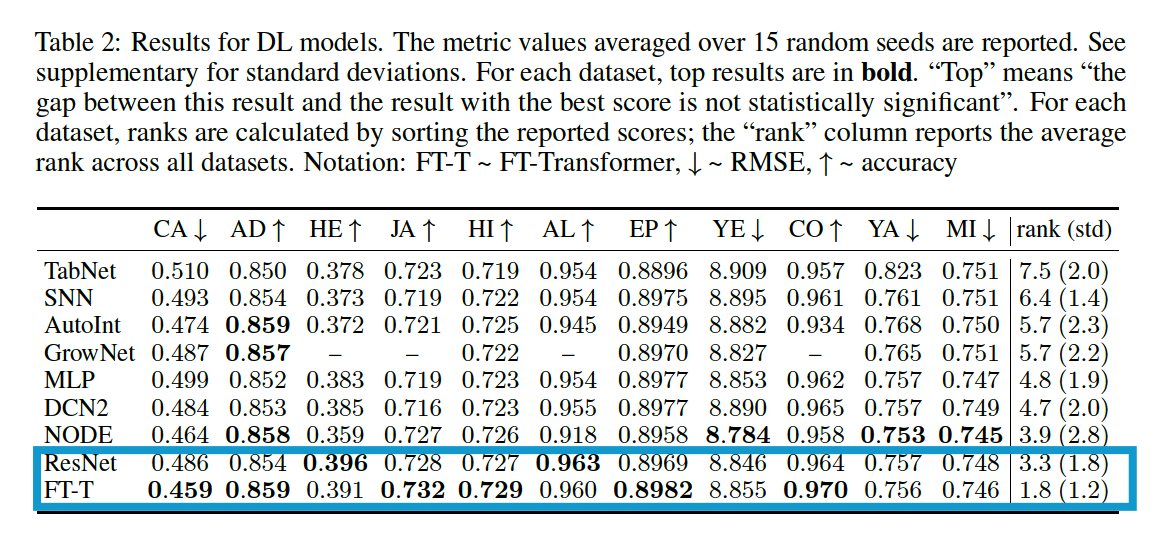
NODE

• high performance, but still inferior to ResNet
• but very complex + not truly a siongle model
  • more params than ResNet & FT-Transformer

Comparing with ENSMEBLE fo DL models

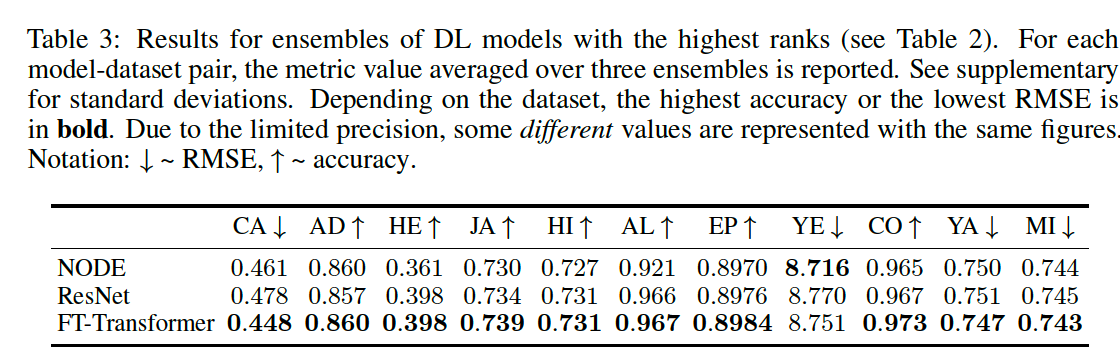
(5) DL vs. GBDT

( compare ensembles instead of single model )

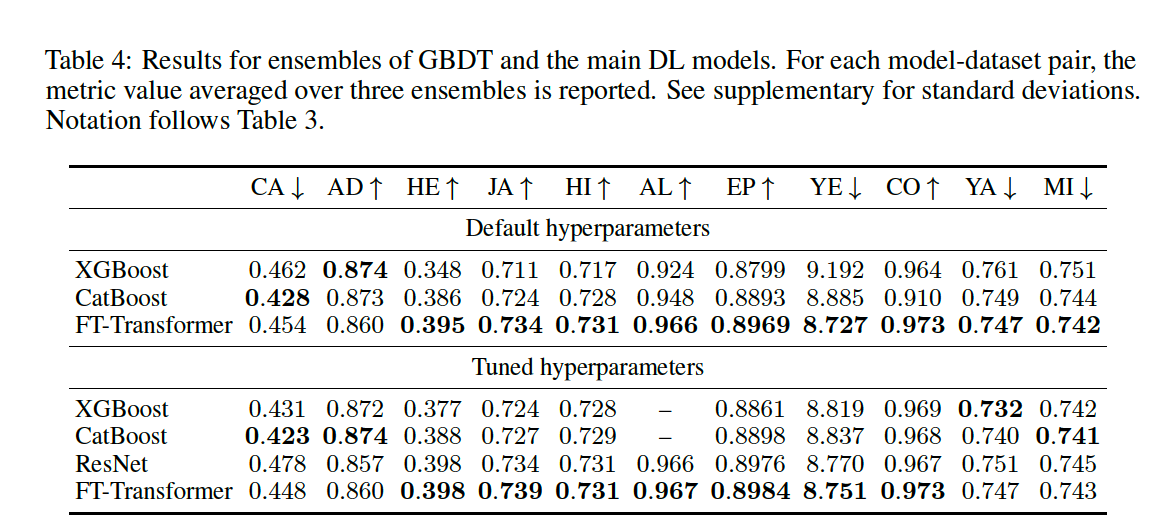
5. Analysis

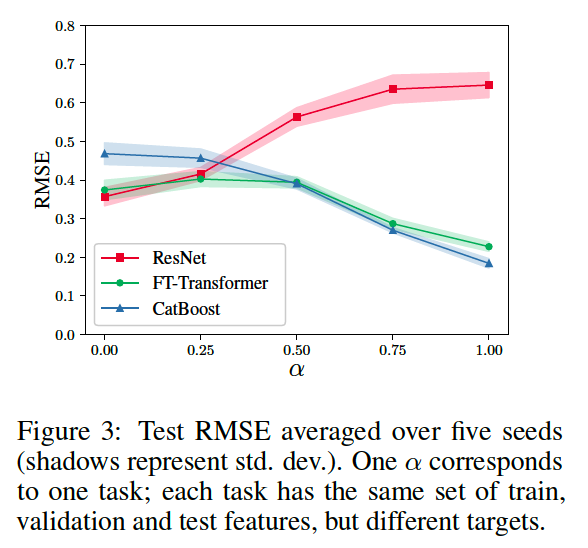
(1) FT-Transformer vs ResNet

make a synthetic test!

• \(x \sim \mathcal{N}\left(0, I_k\right), \quad y=\alpha \cdot f_{G B D T}(x)+(1-\alpha) \cdot f_{D L}(x)\).
• two regression targets
  • \(f_{G B D T}\) : supposed to be easier for GBDT
  • \(f_{D L}\) : expected to be easier for ResNet.

ResNet-friendly tasks

• ResNet and FT-Transformer perform similarly well
• outperform CatBoost

GBDT -friendly tasks

• FT-Transformer yields competitive performance across the whole range of tasks.

(2) Ablation study