A Closer Look at TabPFN v2; Understanding Its Strengths and Extending Its Capabilities

A Closer Look at TabPFN v2: Understanding Its Strengths and Extending Its Capabilities

Ye, Han-Jia, Si-Yang Liu, and Wei-Lun Chao. "A closer look at tabpfn v2: Strength, limitation, and extension." arXiv preprint arXiv:2502.17361 (2025).

arxiv: https://arxiv.org/pdf/2502.17361

Contents

1. Abstract
2. Introduction
3. Related Work
4. Backround
5. Comprehensive Evaluation of TabPFN v2
6. How Does TabPFN v2 Effectively Handle Data Heterogenity
7. TabPFN v2 can be Trasnformed into an Effective Feature Encoder
8. Improving TabPFN v2 via Test-Time Divide-and Conquer
9. Conclusion

Abstract

TabPFN v2

• Advancement in “tabular foundation models”
• Unprecedented “ICL performance” across diverse downstream datasets

This paper = Closer look at TabPFN v2

• How it effectively handles “heterogeneity” and achieves high predictive accuracy
• How its limitations in “high-dimensional, many-category, and large-scale tasks” can be mitigated

Findings

• TabPFN v2 can infer attribute relationships even when provided with randomized attribute token inputs, eliminating the need to explicitly learn dataset-specific attribute embeddings to address heterogeneity.
• TabPFN v2 can be transformed into a feature extractor, revealing its ability to construct a highly separable feature space for accurate predictions
• TabPFN v2’s limitations can be addressed through a test-time divide-and-conquer strategy, enabling scalable inference without requiring re-training.

1. Introduction

Tabular Prior-Fitted Network v2 (TabPFN v2)

• Model) Transformer
• Pretraining) Synthetic datasets
• ICL) Applied to diverse downstream tasks without additional tuning.
• Details
  • Input = Labeled training set and an unlabeled test instance
  • Output = Test label
• Experiments: SoTA on both classification and regression

This paper = understand the mechanisms behind its success

• (1) How it effectively handles dataset heterogeneity and achieves high predictive accuracy
• (2) How to overcome its current limitations
  • Suggested data regime: of no more than 10,000 samples, 500 dimensions, and 10 classes

Major insights

• (1) TabPFN v2 internalizes attribute token learning to handle data heterogeneity

  • Raw input = \(d\) attributes

  • Embedding: Each attribute Into fixed-dimensional tokens

  • Transformer: Handle variability in \(d\)

  • Prior works vs. TabPFN v2

    • Prior works : Rely on known attribute semantics (e.g., word vectors) or learn dataset-specific attribute tokens

    • TabPFN v2: Employs randomized attribute tokens (= resampled at each inference)

      \(\rightarrow\) Allows TabPFN v2 to be directly applied to new downstream datasets with varying dimensionalities and attribute meanings without additional tuning

  • Question) How does it still make accurate predictions?
  • Findings) Regardless of the randomness, TabPFN v2 can consistently infer attribute relationships through in-context learning, essentially integrating attribute token learning into the inference itself.
  • Summary) TabPFN v2 unifies representation learning and prediction within a single forward pass.
• (2) TabPFN v2 can be repurposed as a feature extractor for downstream tasks.
  • Produces instance-level feature representations that are highly discriminative
  • Reveal that TabPFN v2 effectively maps tabular instances into a nearly linearly separable embedding space.
    • Remarkably, training a linear model on these features yields accuracy comparable to that of TabPFN v2’s in-context learner, highlighting its potential as a powerful feature encoder
• (3) Test-time divide-and-conquer effectively mitigates TabPFN v2’s limitations.
  • TabPFN v2 faces challenges when applied to high-dimensional, many-category, or large-scale datasets.
  • These limitations can be effectively addressed through carefully designed post-hoc divide-and-conquer strategies, reminiscent of test-time scaling techniques developed for LLMs

Remark

• In-depth investigation into TabPFN v2
• Contribution lies in the novel analysis and principled extension of TabPFN v2

2. Related Work

(1) Learning with Tabular Data

Skip

(2) Tabular Foundation Models

Challenges of tabular data in foundation models = Heterogeneity

• Variations in attribute spaces, dimensionalities, and label distributions

Solution:

• (1) Leverage the semantic meanings of attributes
  • e.g., “Age is 25, height is 165, …” & apply LLM
• (2) Improve transferability by pre-computing attribute tokens based on semantic embeddings
• (3) TabPFN family
• (4) Meta-learning
  • Generate model weights tailored for downstream tabular tasks with limited data
• (5) Others:
  • Rely on lightweight fine-tuning to adapt to variations in attribute and label spaces

TabPFN family

• Leverages the ICL capabilities of transformers to directly predict labels by contextualizing test instances among training examples.
• Inspired subsequent pre-trained tabular models such as [49, 15, 58]
• TabPFN v1
  • Pads attribute vectors to a fixed dimension
• TabPFN v2
  • Introduces a specialized attribute tokenizer to handle heterogeneous input spaces.

(3) Variants of TabPFN

TabPFN’s success = Stems from its pre-training on massive synthetic datasets

\(\rightarrow\) Strong ICL performance on small-scale classification tasks

Improving scalability of TabPFNs

• By addressing TabPFN’s sensitivity to context size [17, 74].
• Further strategies to enhance downstream performance include context adaptation with nearest neighbor [66], partial fine-tuning [18, 47], pre-training on real-world datasets [49], scalable ensemble [47], and more powerful and efficient pre-training on synthetic data [58].
• Most of these variants remain restricted to classification tasks due to limitations in TabPFN v1.

TabPFN v2 [29]

• Extends TabPFN to support regression tasks and accommodate larger context sizes.

This paper = Comprehensive evaluation of TabPFN v2

3. Background

(1) Learning with a single tabular dataset

Notation

• \(\mathcal{D} = \{(x_i, y_i)\}_{i=1}^N\): dataset
• \(N\) training examples = \(N\) rows
• \(x_i\): \(d\) features or attributes (i.e., columns in the table)
  • \(d\) varies across datasets.
• \(y_i\): label
  • Belongs to \(\{1, \dots, C\}\) for a classification task
  • Numerical value for a regression task

Assumption = All attributes of an instance are numerical (continuous)

• Categorical (discrete) attributes: Transformed using ordinal or one-hot encoding

(2) TabPFN

• Transformer + ICL
• Training and test instances are first zero-padded to a fixed dimension \(k^{'}\) (e.g., 100)
• \(x_i\) and \(y_i\) are linearly projected to \(\tilde{x}_i \in \mathbb{R}^k\) and \(\tilde{y}_i \in \mathbb{R}^k\)
• Input & Output
  • Input = Labeled training set and an unlabeled test instance
  • Output = Test label
• Input ( = Prompt / Context )
  • \(\mathcal{C} = \{ \tilde{x}_1 + \tilde{y}_1, \dots, \tilde{x}_N + \tilde{y}_N, \tilde{x}^* \} \in \mathbb{R}^{(N+1) \times k}\).
  • Consisting of \(N+1\) tokens
  • Processed by multiple transformer layer with variable length inputs ( = variable \(N\) )
• Output token
  • Passed through a MLP

(3) TabPFN v2

Several key modifications.

• Each of the \(d\) attributes in \(\mathcal{D}\) is embedded into a \(k\)-dimensional space

• (1) Random perturbations added to differentiate attributes

• (2) Modification to input?

  • Training instance \(\tilde{x}_i\)

    • \(d+1\) tokens with dimension \(k\) …. with Label embedding \(\tilde{y}_i \in \mathbb{R}^k\)

  • Test instance \(x^*\)

    • Label is unknown … Employ dummy label to generate the label embedding \(\tilde{y}^*\)

      (e.g., the average label of the training set)

  • Shape of input = \((N + 1) \times (d + 1) \times k\)

• (3) Two types of self-attention

  • Over samples (among the \(N + 1\) instances)
  • Over attributes (among the \(d + 1\) dimensions)

• Output token ( = test instance’s dummy label \(\tilde{y}^{*}\) )

  • Extracted and mapped to a …
    • (1) \(C\)-class logit for classification
    • (2) Single-value logit for regression.

Pretraining

Pre-trained on diverse synthetic datasets generated using structural causal models (SCMs)

(4) Remark

(Note that many technical details were omitted from the main paper)

Example) Use of randomized tokens was documented in the supplementary material and code

4. Comprehensive Evaluation of TabPFN v2

Extend TabPFN v2’s evaluation (beyond the original set of datasets) to over 300!

• Much broader range of domains, attributes, scales, dimensionalities, and tasks

(1) Setups

Benchmark from [76]

• 120 binary classification
• 80 multi-class classification
• 100 regression

Issues

• Mislabeled data
• Redundancies from overlapping dataset

Split

• Out of the 300 datasets,
• 27 belong to the validation set used for checkpoint selection in TabPFN v2

\(\rightarrow\) To avoid evaluation bias, we exclude these datasets and report results on the remaining 273 datasets.

Each dataset is randomly split into training, validation, and test partitions in a 64%/16%/20% ratio!

TabPFN v2

• Predicts test set labels directly using ICL

  (w/o any additional parameter or hyperparameter tuning)

Metrics

• 15 random seeds ( report the average performance )
• Classification = Acc.
  • with more than 10 classes: Error-Correcting Output Codes (ECOC)
• Regression = RMSE

(2) Strengths of TabPFN v2

• Baseline: 26 representative tabular methods

• Test: Statistical significance test (Wilcoxon-Holm test) .. Figure 1 (right)

• Results: Consistently outperforms both ..

  • (1) Tree-based methods

  • (2) Deep tabular models

(3) Limitations of TabPFN v2

Above evaluation = Focuses on small- to medium-scale datasets

• Fewer than 10,000 examples

Computational complexity of transformers

\(\rightarrow\) Constrains TabPFN v2’s ability to scale effectively to datasets with larger sample sizes or higher dimensionality!

Large scale datasets: Conduct additional evaluations on …

• (1) 18 high-dimensional datasets with \(d \geq 2000\)
• (2) 18 large-scale datasets where \(N \times d > 1,000,000\)

(1) High-dimensional datasets

• Follow the same protocol as before

(2) Large-scale datasets

• Due to the prohibitive cost of hyperparameter tuning…

  \(\rightarrow\) Default hyperparameters are used for all methods

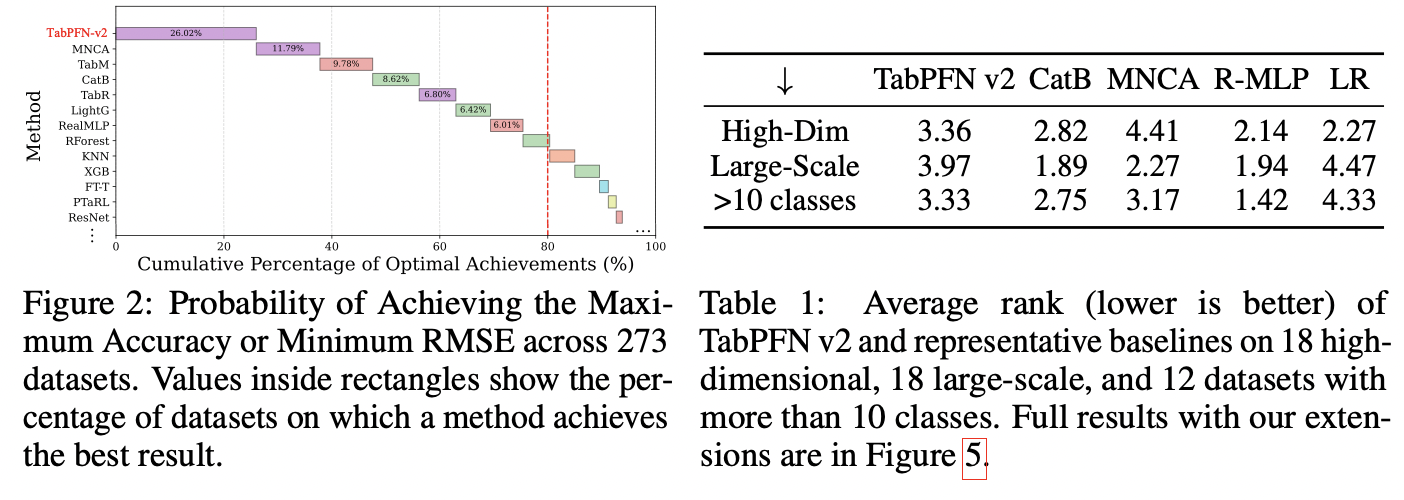
Results: Performance degrades on both large-scale and high-dimensional datasets

(1) High-dimensional datasets

• Ranks below both CatBoost and RealMLP

(2) Large-scale datasets

• Falls behind the simple Logistic Regression (LR) model.

(3) More than 10 categories

• ECOC strategy currently used by TabPFN v2 appears ineffective in achieving high accuracy

• Pre-trained exclusively on small- to medium-scale synthetic datasets with fewer than 10 categories,

  \(\rightarrow\) Leading to a mismatch when applied to larger or more complex real-world data!

5. How Does TabPFN v2 Effectively Handle Data Heterogenity

• Examine the mechanisms behind its strengths
• Methods to overcome its limitations

(1) Diving into TabPFN v2’s Mechanisms for Heterogeneous Input

a) Revisiting the problem

Robust tabular foundation model

\(\rightarrow\) Must handle heterogeneity effectively

\(\rightarrow\) Enable to learn from diverse pre-training datasets & transfer its capabilities to new downstream tasks

b) Tokenization as a feasible solution

Token-based methods

• (From) \(d\)-dimensional instance \(x \in \mathbb{R}^d\)

• (To) Set of \(d\) fixed-dimensional tokens (each of dimension \(k\))

  • One token per attribute

• Enables the use of transformer architectures

  ( & Accommodate variability in \(d\) across datasets )

Embedding

• Embed each attribute into a shared \(k\)-dim space
• (Previous works) Either uses ..
  • (1) pre-defined semantic embeddings (e.g., word vectors of attribute names)
  • (2) Dataset-specific embeddings
• Notation:
  • \(d\) attribute-specific tokens \([r_1, \dots, r_d] \in \mathbb{R}^{d \times k}\) .
  • (Before) \(x_i \in \mathbb{R}^d\)
  • (After) \([x_i^1 \cdot r_1, \dots, x_i^d \cdot r_d] \in \mathbb{R}^{d \times k}\).
    • where \(x_i^j\) denotes the \(j\)-th element of \(x_j\)

c) Difficulty in direct generalization

Aforementioned methods: Face a notable challenge when applied to downstream tasks!!

\(\rightarrow\) Attribute names or semantics are not always accessible!!

d) TabPFN v2’s mechanisms

Also builds on (prior) token-based methods

• Represent each instance \(x_i\) as a sequence of tokens

Rather than assigning a deterministic token to each attribute …

\(\rightarrow\) TabPFN v2 samples random tokens at inference time!

Adding random tokens?

• Learns a shared vector \(u \in \mathbb{R}^k\) that lifts each element of \(x_i\) into a \(k\)-dimensional space
• To distinguish attributes, TabPFN v2 adds a random perturbation to each one
• Details
  • \(j\)-th attribute (i.e., \(x_i^j\)), the representation becomes …
  • \(x_i^j \cdot u + r_j\) where \(r_j = W p_j\)
    • \(p_j \in \mathbb{R}^{k'}\): Randomly generated vector
    • \(W \in \mathbb{R}^{k \times k'}\): Learned projection matrix that conditions the perturbation
  • Full instance \(x_i\)
    • \([x_i^1 \cdot u + r_1, \dots, x_i^d \cdot u + r_d, \tilde{y}_i] \in \mathbb{R}^{k \times (d+1)}\).
      • where the last token \(\tilde{y}_i\) encodes the label information

(2) TabPFN v2 Internalizes Attribute Token Learning

“Randomized” tokenization scheme

\(\rightarrow\) Eliminates the need to define attribute- or dataset-specific tokens across tasks!

\(\rightarrow\) Enabling direct application of the pre-trained model to any dataset

(At first glance)

• May appear to disregard the valuable semantic meaning of attributes.

(However)

• Show that through ICL, TabPFN v2 can consistently infer relationships among attributes within a dataset

Analysis

• From three perspectives
• Using two representative downstream datasets

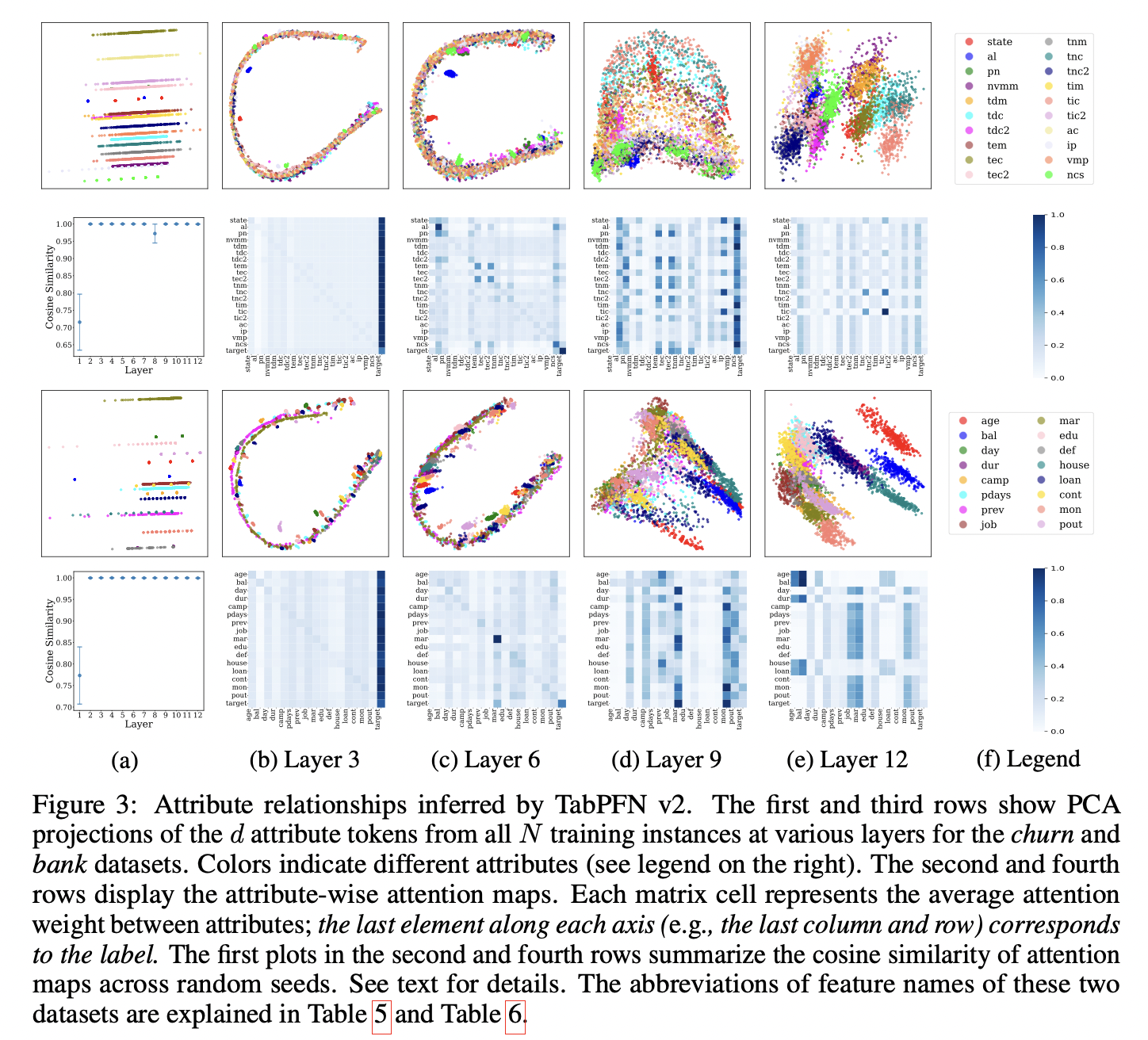
Remark

TabPFN v2 can reliably infer meaningful attribute relationships through ICL

Although input embeddings are randomized…

\(\rightarrow\) Consistently differentiate attributes across instances!

6. TabPFN v2 can be Transformed into an Effective Feature Encoder

TabPFN v2’s ICL process infers meaningful attribute relationships

( = Effective feature encoder )

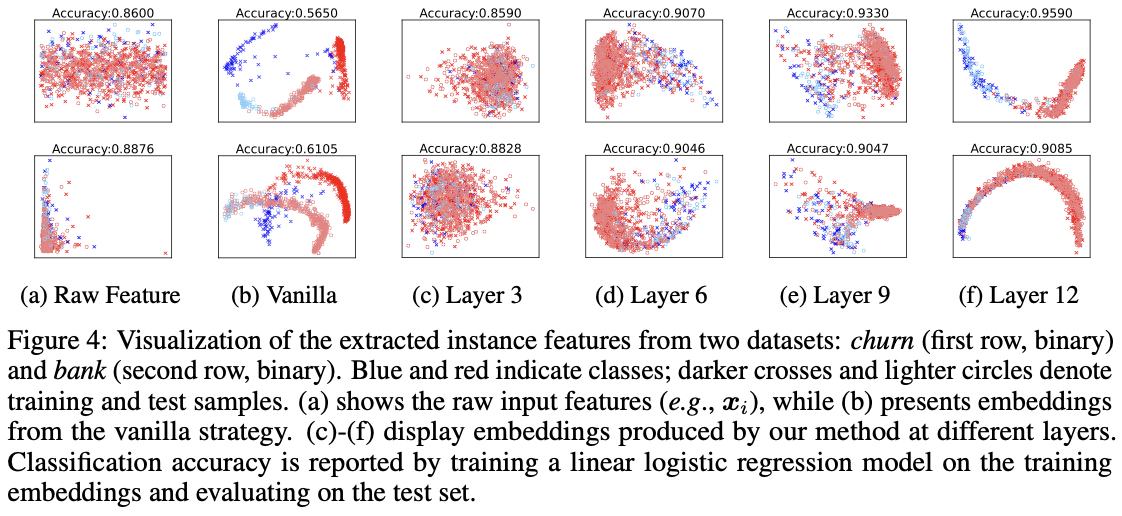
(1) Naive Feature Extraction Fails

[Figure 1] Prediction of TabPFN v2

• Based on the output token
  • Corresponding to the (dummy) label embedding $\tilde{y}^*$
• $\therefore$ Output token = Interpreted as the instance embedding for the test example

[Figure 4-(b)] Discrepant feature distributions between …

• Training (darker cross)
• Test (lighter circle)

$\rightarrow$ Linear classifier trained on these embeddings performs poorly on the test set

• Reason: Mistmatch btw training & test
  • Distinct roles of (labeled) training data and (unlabeled) test data in TabPFN v2’s ICL process

(2) Leave-on-fold-out Feature Extraction

Solution: Leave-one-fold-out strategy

• Enables the extraction of “comparable” embeddings for training & test data

Notaton

• $\mathcal{S}$: “Support” set = Examples with true labels ( = TRAIN )
• $\mathcal{Q}$: “Query” set = Examples with dummy labels ( = TEST )

To extract comparable embeddings for the training examples ($\mathcal{S}$)…

• $\mathcal{S}$ must also be included in $\mathcal{Q}$ with dummy label embeddings

$\rightarrow$ Causes dilemma!

Dilemma?

Effective ICL relies on maximizing the size of $\mathcal{S}$ to ensure sufficient knowledge transfer to $\mathcal{Q}$

• Including training examples in $\mathcal{Q}$ thus competes with the need to keep $\mathcal{S}$ as large as possible

Solution: Partition the training set into multiple folds (e.g., 10)

Details: In each round…

• [One fold] Serves as $\mathcal{Q}$ —with dummy labels used for embedding extraction
• [Remaining folds] Form $\mathcal{S}$ with true labels

[Figure 4-(c–f)] Leave-one-fold-out strategy

• Embeddings extracted by this strategy (with 10 folds) more faithfully capture dataset structure
• Especially after intermediate layers

(3) Validation of Embedding Quality

Evaluation of the quality of the embeddings

$\rightarrow$ Train a logistic regression on embeddings (Table 2)

• Train: with the training embeddings
• Evaluation: with test set embeddings

Result

• Comparable to that of TabPFN v2’s in-context learner.
• Concatenate embeddings from multiple layers can sometimes lead to better results

7. Improving TabPFN v2 via Test-Time Divide-and-Conquer

(Post-hoc) Divide-and-conquer strategies

• Inspired by CoT prompting
• Decompose challenging tasks into simpler subtasks!

(1) High Dimension Datasets

[1] Challenge: “Quadratic” complexity of TabPFN v2 w.r.t. dimension

[2] Solution: Subsampling the feature space (into smaller subsets)

• Process each subset independently
• Combine the predictions in an ensemble fashion

[3] Procedures

• Step 1) Iteratively sample $m$ subsets
  • Each containing $d’ < d$ randomly selected attributes
• Step 2) For each subset…
  • Leverage TabPFN v2’s ability to handle lower-dimensional data to obtain predictions
• Step 3) Ensemble
  • Aggregates outputs using averaging (for regression) or majority voting (for classification)

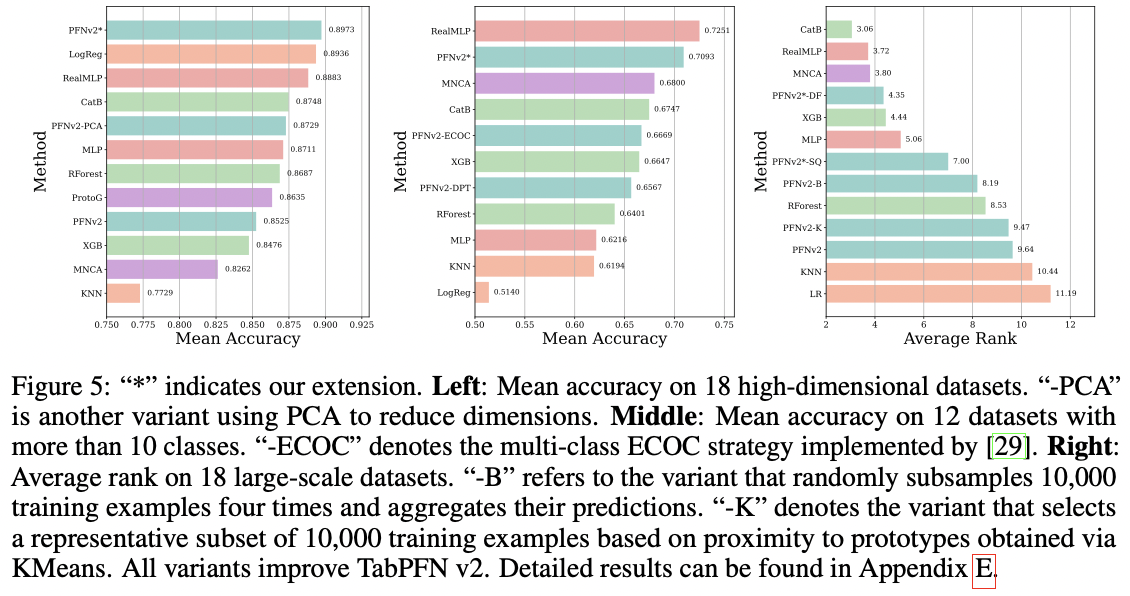
[Figure 5-(left)] 18 High-dimensional CLS datasets

• PFNv2-*: Divide-and-conquer + Ensemble
• PFNv2-PCA: PCA for dimensionality reduction

(2) Multi-Class Problems with More Than 10 Classes

[1] Challenge: Datasets with more than 10 categories

[2] Solution: Decimal encoding approach (TabPFN v2-DPT)

• Decomposes multi-class problems into multiple 10-class subproblems

[3] Procedures

• Step 1) For a task with $C > 10$ classes…
  • Encode each label $y \in [C] $ as a $t$-digit decimal representation, where $t = \lceil \log_{10} C \rceil$
• Step 2) For each digit position $j \in {1, \dots, t}$ )
  • Train a separate TabPFN v2 model $f_j$ to predict the $j$-th digit.
• Step 3) Inference
  • Predicted digits are reconstructed to obtain the final class label

[Figure 5-(middle)] 12 datasets with more than 10 classes

(3) Large-Scale Datasets

[1] Challenge: Large-scale datasets

[2] Solution: Random sample v1 (TabPFN v2∗-SQ)

[3] Procedure

• Step 1) Support set & Query set
  • Support set: Randomly sample 10,000 training examples from the full training set
  • Query set: Remaining training examples and test instances as the query set
• Step 2) Extract their embeddings $\rightarrow$ Form a new tabular dataset
• Step 3) Train a logistic regression classifier
• Step 4) Inference: Repeat x 4 times & aggregate

[2] Solution: Random sample v2 (TabPFN v2∗-DF)

[3] Procedure

• Step 1) Sample 32 subsets from the original training set
  • Each containing 60% of the original data (sampled without replacement)
• Step 2) For each subset, Train a shallow decision tree
  • Setting the minimum number of samples required to split an internal node to 10,000
  • Decision tree partitions the training set into smaller, more manageable subsets
• Step 3) Predictions from all 32 models are aggregated. We

8. Conclusion

TabPFN v2 = Foundation model for tabular tasks

Uncovers the core mechanism behind TabPFN v2

Findings & Proposal

• Can infer attribute relationships on-the-fly
  • w/o relying on pre-defined semantics or learning dataset-specific representations
• Can be repurposed as a powerful feature encoder
• Ppost-hoc divide-and-conquer strategies
  • Extend TabPFN v2’s utility without requiring model re-training