TabFlex; Scaling Tabular Learning to Millions with Linear Attention

TabFlex: Scaling Tabular Learning to Millions with Linear Attention

Zeng, Yuchen, et al. "Tabflex: Scaling tabular learning to millions with linear attention." ICML 2025

arxiv: https://www.arxiv.org/pdf/2506.05584

code: https://github.com/microsoft/ticl

Abstract

Recent trends: In-context learning (ICL) capability LLMs for Tabular Classification

\(\rightarrow\) “Training-free adaptability” across diverse datasets!

(Recent works) TabPFN

• Excel in tabular “small-scale” datasets
• Struggle to scale for “large and complex” datasets

(Proposed) TabFlex

• Enhances the efficiency and scalability of TabPFN for “larger datasets”
• Idea) Linear attention
• Datasets) With thousands of features and hundreds of classes
• Experiments)
  • 2 x speedup (vs. TabPFN)
  • 1.5× speedup (vs. XGBoost)

1. Introduction

(1) Transformers for tabular

FT transformer (Gorishniy et al., 2021)

• Converts each sample into embedding via Transformer

TabTransformer (Huang et al., 2020)

• Learns embeddings for categorical features
• Concatenate with numerical features

LIFT (Dinh et al., 2022)

• Converts tabular data into LLM inputs
• How? By combining with feature names and task descriptions (into textual sentences)

\(\rightarrow\) (Compared to GBDT) Suffer from high latency overhead

(2) TabPFN (Hollmann et al., 2023)

Handles latency limitations of Transformer-based methods using ICL of LLMs

• (1) w/o parameter updates

• (2) Superior efficiency & performance on small-scale datasets

• (3) Incorporates all training and testing samples into a “single prompt” & classifies the testing samples in “one forward pass”

  \(\rightarrow\) Highly effective on “simple and small” tabular datasets

Limitation: Suffer with complex (& large) datasets

\(\because\) Quadratic complexity of the attention mechanism

(3) Proposal: TabFlex

Handles the limitations of the scalability of TABPFN

\(\rightarrow\) Improve the effectiveness of Transformer-based methods for “tabular classification”!!

Analyze scalable alternatives to attention mechanisms

• e.g., Mamba, Linear Attention

Findings

• (Finding 1) Inherent causality of SSMs
  • Impedes ICL performance compared to “non-causal” mechanisms
• (Finding 2) “Linear attention” does not suffer from this limitation!

\(\rightarrow\) Develop TabFlex leveraging linear attention

2. Related Works

(1) Transformer-based approaches for tabular classification

Phase 1.

TabNet (Arik & Pfister, 2021)

• Unsupervised pre-training on masked tabular datasets to infer missing features

TabTransformer (Huang et al., 2020)

• Handles categorical features by concatenating their contextual embeddings into numerical features

FT-Transformer (Gorishniy et al., 2021)

• Converts samples to embedding sequences using a feature tokenizer for the transformer

LIFT (Dinh et al., 2022)

• Converts each sample into a sentence
  • with a predefined template incorporating the task description and feature names
• Make it as a natural input to apply ICL in LLM

TabR (Gorishniy et al., 2024)

• Retrieval-augmented model with a custom kNN-like component
• Retrieve and extract signals from the nearest neighbors

BiSHop (Xu et al., 2024)

• Establishes interconnected directional learning modules to process data column-wise and row-wise for tabular learning

XTab (Zhu et al., 2023)

• Independent featurizers and federated learning to resolve inconsistent column types and quantities.

Phase 2.

TabPFN (Hollmann et al., 2023)

• Trained offline on synthetic datasets
• Efficient inference in small-scale tabular classification tasks
• Limited to small tabular classification datasets

Phase 3.

MixturePFN (Xu et al., 2025)

• Improves scalability by routing new test samples to a pool of scalable prompters using Sparse Mixture of In-Context Prompters

LoCalPFN (Thomas et al., 2024)

• Retrieve a local subset of task-specific data for efficiently fine-tuning on

Ma et al. (2024)

• In-context data distillation to optimize TabPFN’s context and remove the data size constraint

TuneTable (Feuer et al., 2024)

• Scales TabPFN to large datasets by performing a prefix tuning per dataset

TabPFNv2 (Hollmann et al., 2025)

• Enhances TabPFN’s accuracy in low-data regimes (fewer than 10,000 samples)

This paper

Based on TabPFN

Extend its scalability to large datasets while maintaining and improving efficiency

\(\rightarrow\) By simply replacing the softmax attention with linear attention!

(2) Attention mechanisms and scalable alternatives

Skip

3. Preliminaries

(1) Implementation of ICL in TabPFN

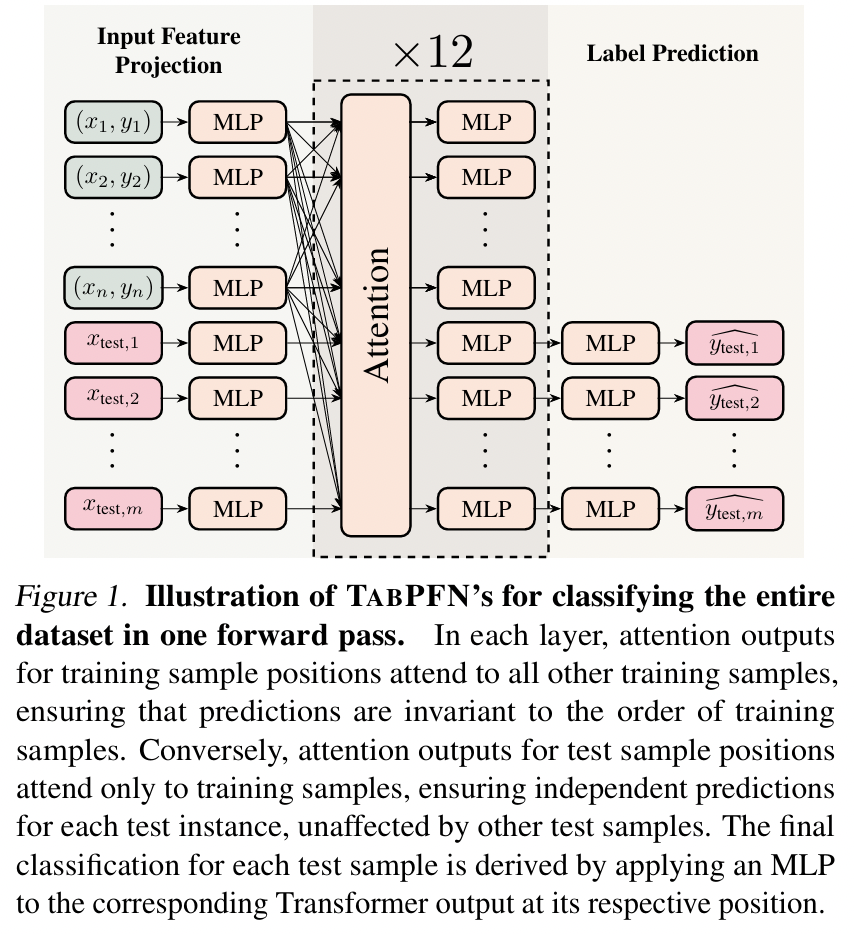
a) Data

• Each sample = Token

• Tokens = Starting with training samples \(\rightarrow\) Followed by testing samples

b) Embedding

• (Training samples) Features \(X\) & Labels \(y\)
• (Testing samples) Features \(X\)

\(\rightarrow\) Embedded with MLPs before being concatenated

c) Attention

• Computed by attending to all other training samples
• Outputs for test sample positions attend only to the training samples

d) Predictions

• Generated by projecting the Transformer outputs at test positions into probability distributions

e) Comparison with standard ICL

Standard ICL

• Requires \(m\) (number of test samples) separate prompts

  \(\rightarrow\) Requires \(m\) prediction passes

ICL of TabPFN

• Encoder with non-causal attention

• Allowing outputs within training sample positions to interact freely!

  \(\rightarrow\) Requires single prediction passes

(2) Mamba

Skip

(3) Linear Attention

Notation

• Sequence with length \(n \in \mathbb{N}^+\)
• Embedding size \(d \in \mathbb{N}^+\)
• Query, Key, Value (at \(i\)-th position)
  • \(q_i \in \mathbb{R}^d\), \(k_i \in \mathbb{R}^d\), \(v_i \in \mathbb{R}^d\) , where \(i = 1, \ldots, n\).

Softmax attention

• Similarity between \(q_i\) and \(k_j\) = \(\exp(q_i^\top k_j)\).

• Attention output \(a_i \in \mathbb{R}^d\): Averaging the values across all tokens weighted by their similarities

  \(\rightarrow\) Requires \(\mathcal{O}(n)\) complexity

  ( \(\because\) Necessitates computing similarities with all \(n\) tokens )

Linear attention

• Goal: Reduce the complexity of Softmax attention
• How? By replacing the similarity computation from (a) \(\rightarrow\) (b)
  • (a) \(\exp(q_i^\top k_j)\)
  • (b) \(\phi(q_i)^\top \phi(k_j)\)

Linear attention outputs (\(a_i\)) across all positions:

• \(\sum_{j=1}^n \phi(k_j) \cdot v_j\) & \(\sum_{j=1}^n \phi(k_j)\)

  \(\rightarrow\) Can be computed once

  \(\rightarrow\) Only need to compute \(\phi(q_i)\) & multiply it with these two statistics

  \(\rightarrow\) Requires \(\mathcal{O}(1)\) complexity!

Comparison

• (Softmax) \(a_i = \frac{\sum_{j=1}^n \exp(q_i^\top k_j) \cdot v_j}{\sum_{j=1}^n \exp(q_i^\top k_j)}\)

• (Linear) \(a_i = \frac{\phi(q_i)^\top \sum_{j=1}^n \phi(k_j) \cdot v_j}{\phi(q_i)^\top \sum_{j=1}^n \phi(k_j)}\)

For causal cases (the above was for “non-causal” cases)

\(\rightarrow\) Replace \(\sum_{j=1}^n\) with \(\sum_{j=1}^i\)

Interpretation

• Statistics become \(\sum_{j=1}^{i-1} \phi(k_j) \cdot v_j\) and \(\sum_{j=1}^{i-1} \phi(k_j)\)

  = Can be viewed as hidden states in RNNs

• Causal linear attention \(\approx\) linear RNN

4. Architectural Exploration for Scalable Tabular Learning

SSM & Linear attention

\(\rightarrow\) Architecture alternatives to enhance the scalability of TabPFN!

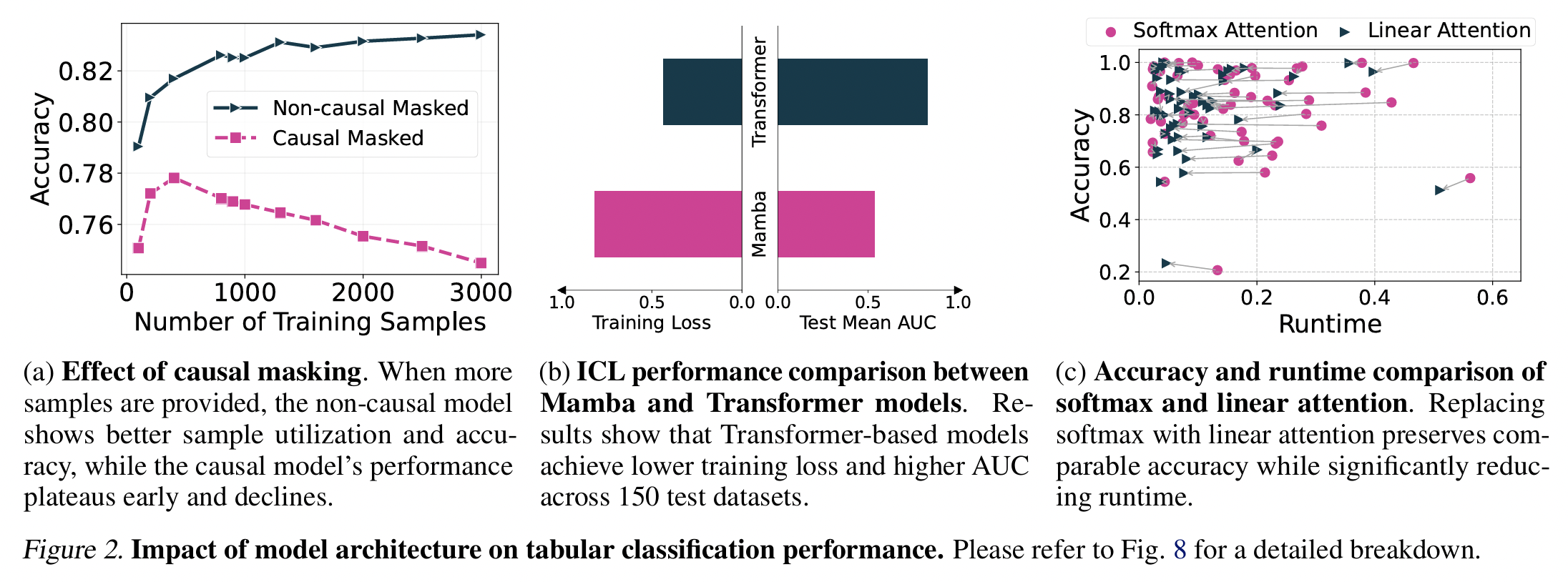
• (Figure 2-a) Section 4-1 (a)
• (Figure 2-b) Section 4-1 (b)
• (Figure 2-c) Section 4-2

(1) Causal Model vs. Non-Causal Model

Tabular data: non-sequential

SSMs: Inherently causal

\(\rightarrow\) Potential drawback in this context :(

Conduct two experiments,

to show suboptimal performance of causal models in Tabular ICL

• (a) Causal Attention vs. Non-Causal Attention
  • Comparing the performance of TABPFN with a modified version of the same model that uses causal attention
• (b) Mamba vs. Transformer
  • Evaluating TABPFN against both its original version and a model incorporating Mamba-II

(a) Causal Attention vs. Non-Causal Attention (Figure 2-a)

Findings:

• “Non-causal” attention generally outperforms “causal” attention
• As more training samples are given …
  • Accuracy of the non-causal model continues to improve
  • Accuracy of the causal model continues to improve \(\rightarrow\) decline

Summary

• TABPFN with “non-causal” attention functions as an effective ICL model
• Supported by empirical studies which show that causal attention is suboptimal for ICL (Ding et al., 2024; Gong et al., 2023)

(b) Mamba vs. Transformer (Figure 2-b)

Findings: Model with Mamba exhibits …

• Significantly higher training loss than the original TABPFN

• ,Substantially lower test mean AUC

\(\rightarrow\) SSMs underperform non-causal models!

(2) Softmax Attention vs. Linear Attention (Figure 2-c)

Findings

• Linear attention does not decrease performance

• Linear attention significantly improves speed

  \(\rightarrow\) Suitable method for scaling TABPFN to larger datasets!

5. TabFlex: Scaling TabPFN for Large Datasets

(Findings in Section 4) Non-causal linear attention is a strong alternative to standard attention!

Two parts

• (1) Thorough analysis of the linear attention mechanism
• (2) Leverage this efficient implementation to train TabFlex

(1) Computation Analysis

Skip

(2) TabFlex

a) TabPFN

• Excels on small, simple datasets

  ( with fewer than 100 features and 10 classes )

• Struggles with more complex tasks

  ( high-dimensional datasets or those with numerous classes )

b) Three specialized versions

TabFlex-S100

• S = Standard configuration
• 100 = Feature capacity (For low-dimensional datasets)
• Prompts with 1152 length (same as TabPFN), 100 features, 10 classes

TabFlex-L100

• L = Larger sample size
• 100 = Feature capacity (For low-dimensional datasets)
• Prompts with 50K length, 100 features, 10 classes

TabFlex-H1K

• H = High-dimensional datsaets
• 1000 = Feature capacity
• Prompts with 50K length, 1K features, 100 classes

c) Conditional model selection strategy

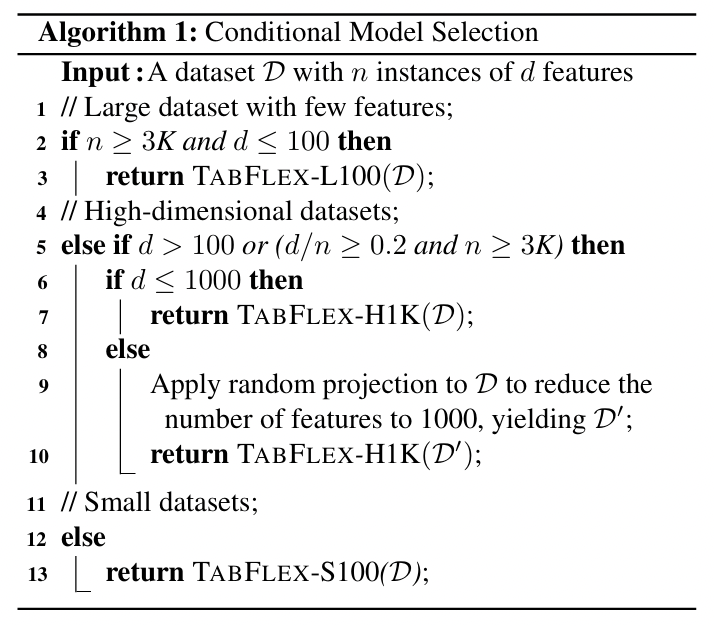
(Section C-4) Performance is not highly sensitive to the chosen decision boundaries!

d) TabPFN vs. TabFlex

Mean runtime & Mean AUC comparison

• On validation datasets (comprising 40 datasets with varying sample sizes)

6. Performance Evaluation of TabFlex

Datasets

115 OpenML tabular datasets

(1) Experimental Setup

Baselines

• a) Four classical methods
• b) Three GBDT methods
• c) Ten Non-Transformer NN
• d) Two recent methods designed for scaling tabular classification
  • TuneTables (Feuer et al., 2024)
  • HyperFast (Bonet et al., 2024)

(2) Evaluation on Simple Datasets

Two sets of data

• a) 98 simple datasets
• b) 57 small datasets

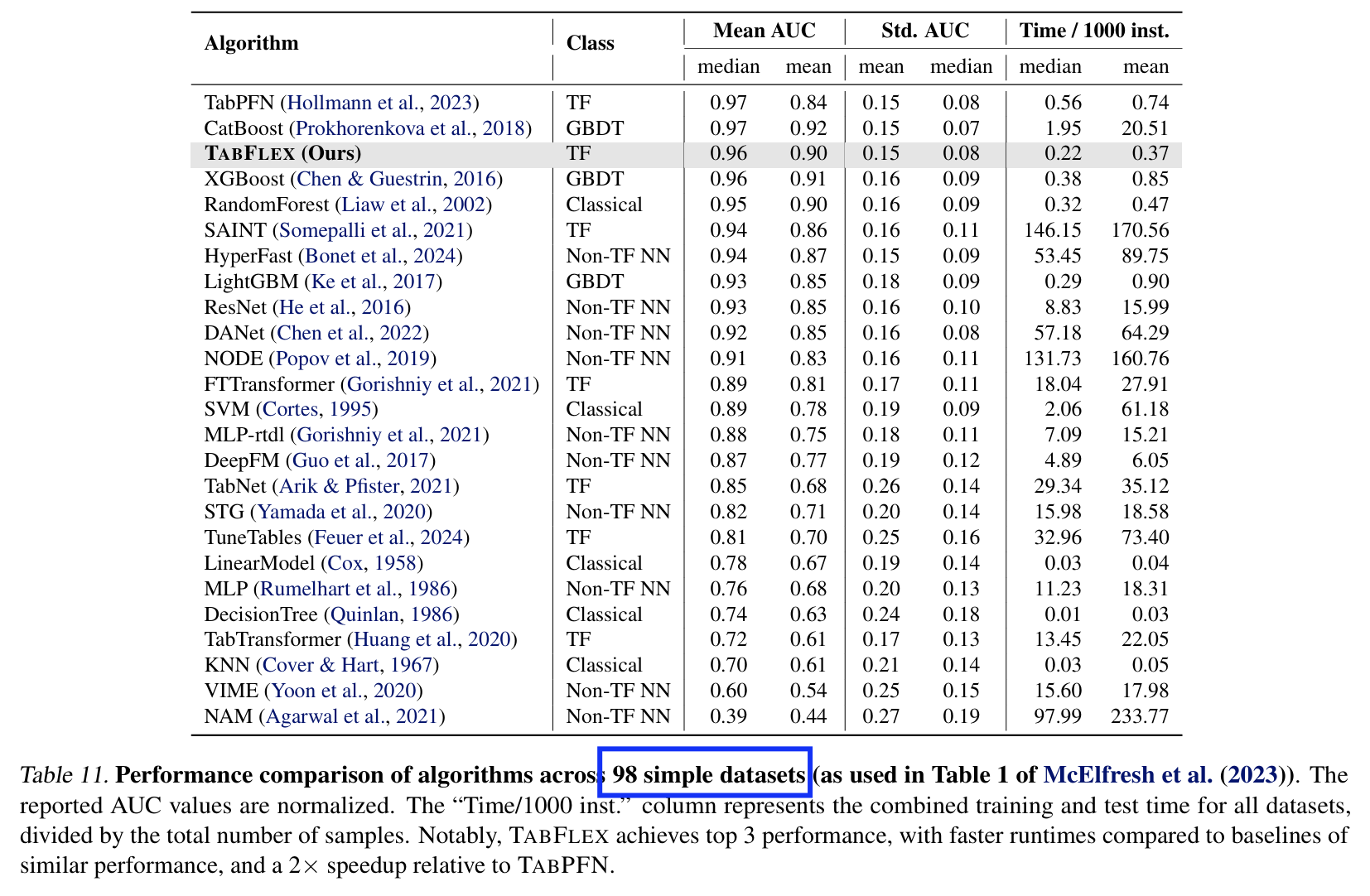
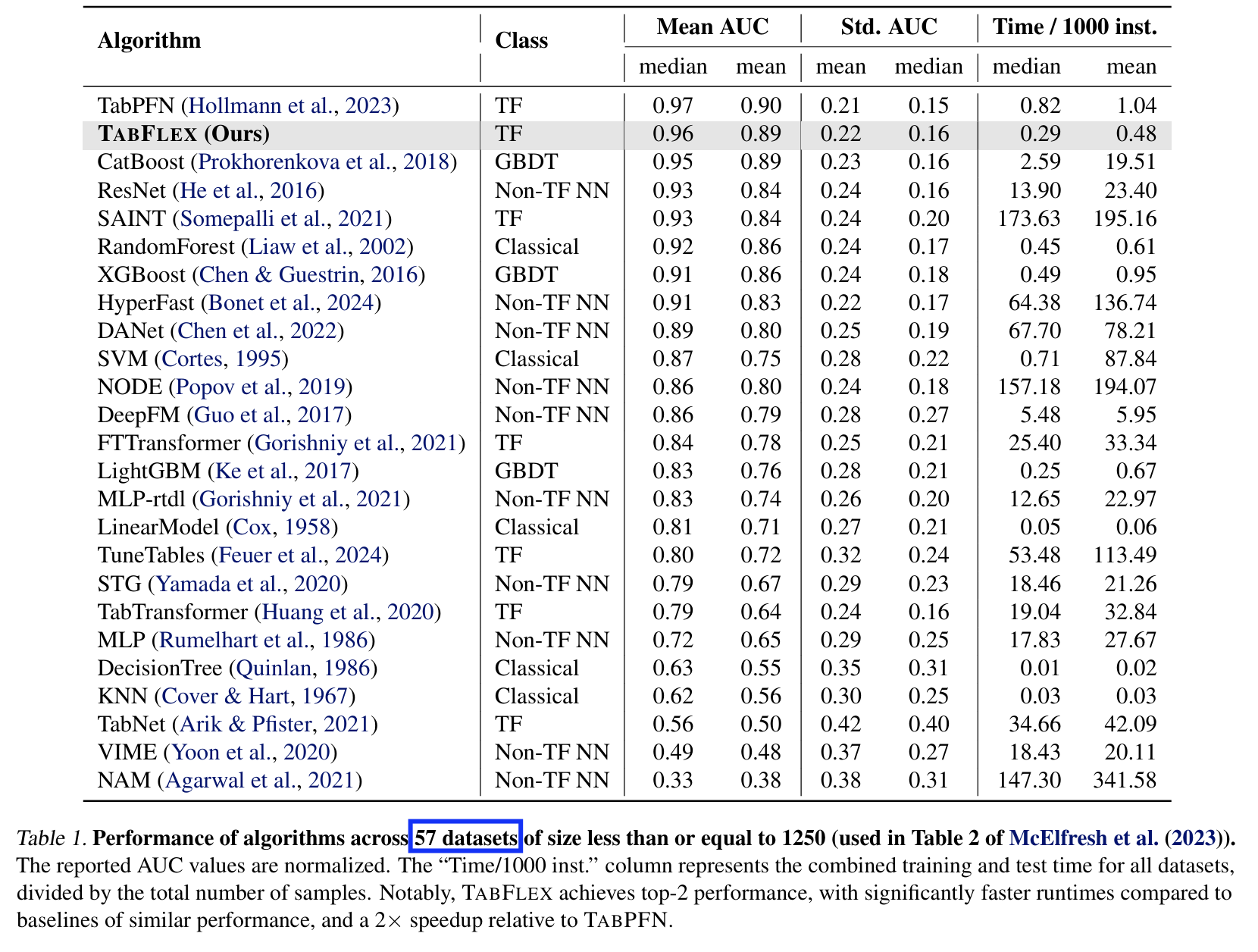
Details

• (Per datasets)
  • Ten different train/test splits \(\rightarrow\) Mean & Std
  • Total runtime per 1000 instances
• (Overall)
  • Median & Mean across datasets
  • Table 11 & Table 1
• Rank: Based on AUC and time

Results

• (vs. TabPFN)
  • Performance: nearly identical
  • Speed: More than 2 x speedup
• (vs. Other methods)
  • Performance: superior

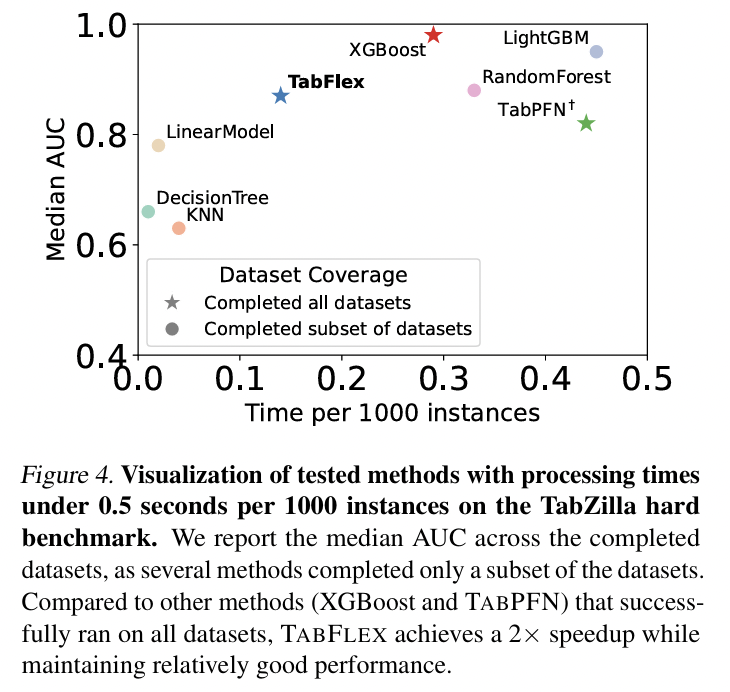
(3) Evaluation on Hard Datasets

Datasets: TabZilla hard benchmark (McElfresh et al., 2023)

• Includes 36 datasets

Hard datasets \(\rightarrow\) Many baselines fail to execute successfully!

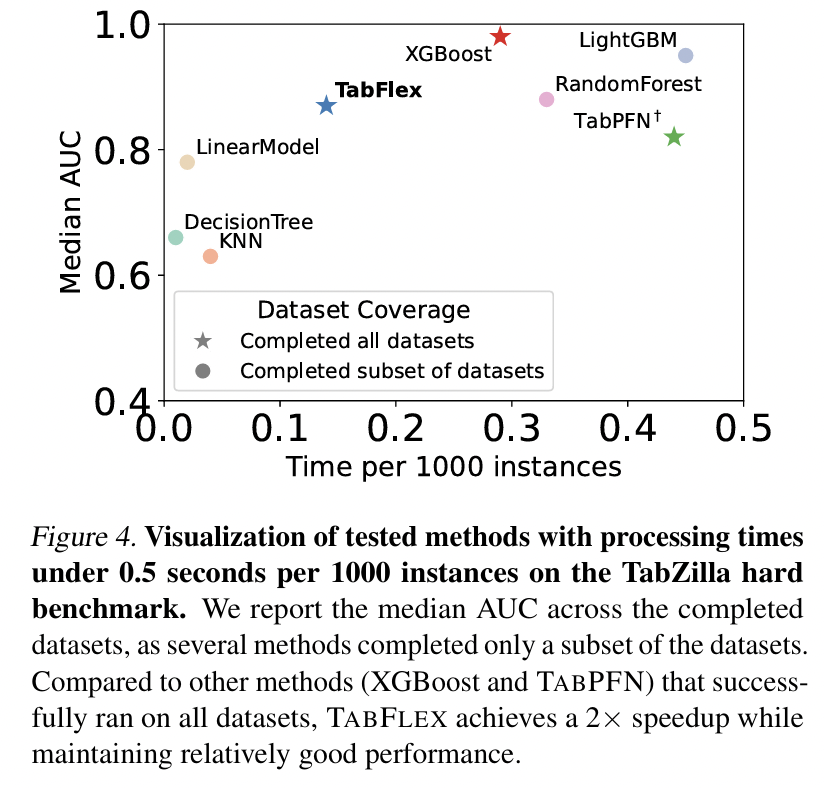
• Median AUC & Runtime per 1000 instances across the 36 datasets
  • Stars = Methods that successfully executed on all datasets
  • Circles = Methods that failed to execute on some datasets
• Focuses on efficient methods
  • Exclude those slower than 0.5 secs per 1000 instances
• Findings: Only TabFlex, TabPFN, XGBoost run successfully!

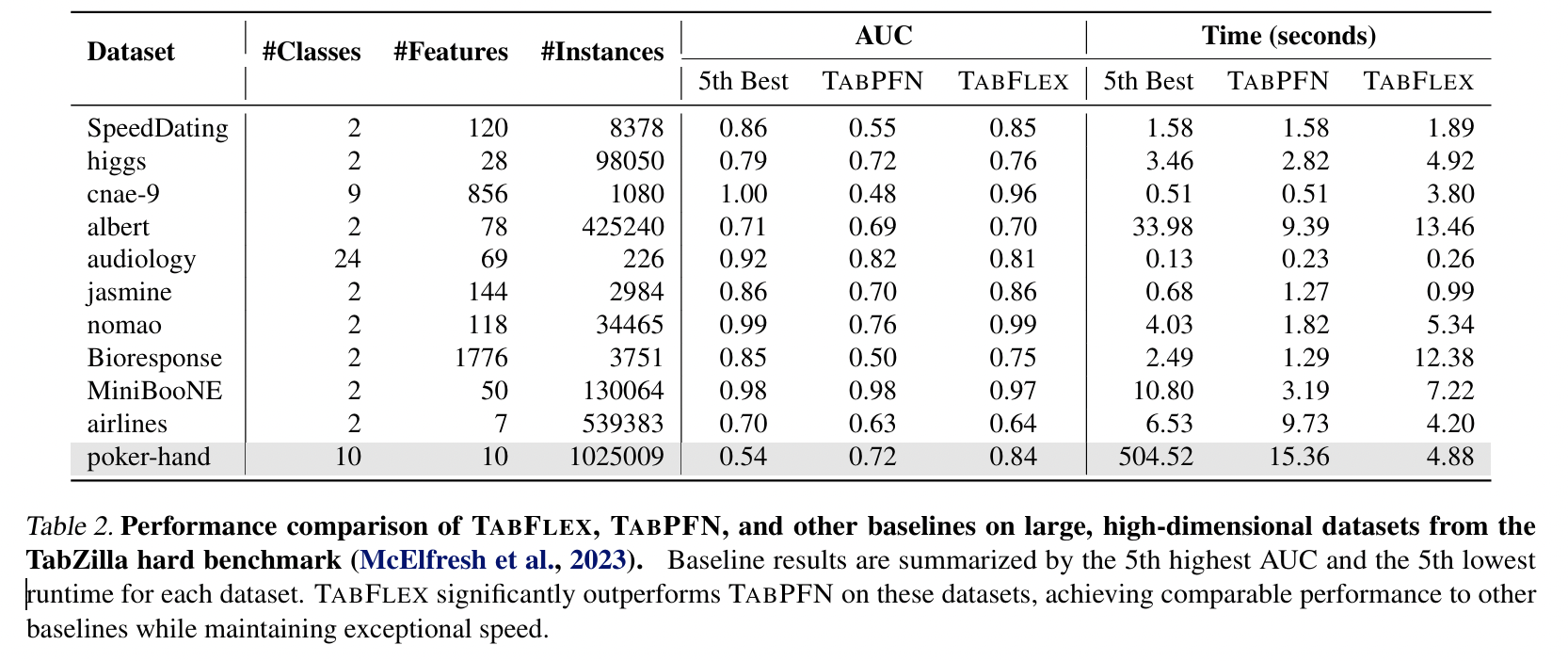
• Focus on 11 high-dimensional and large datasets TabZilla hard benchmark

• As most baselines do not obtain complete results for all datasets…

  \(\rightarrow\) Report the 5th-best AUC and 5th-best runtime

• Findings:

  • TabFlex substantially outperforms TabPFN!
  • With more than 50K instances, TabFlex is significantly faster than the baselines!
    • e.g., poker-hand: over 1M samples

(4) Extension to Regression Tasks

Convert the task into classification by discretizing the target range into bins!

• Targets are discretized into 10 and 100 uniform bins

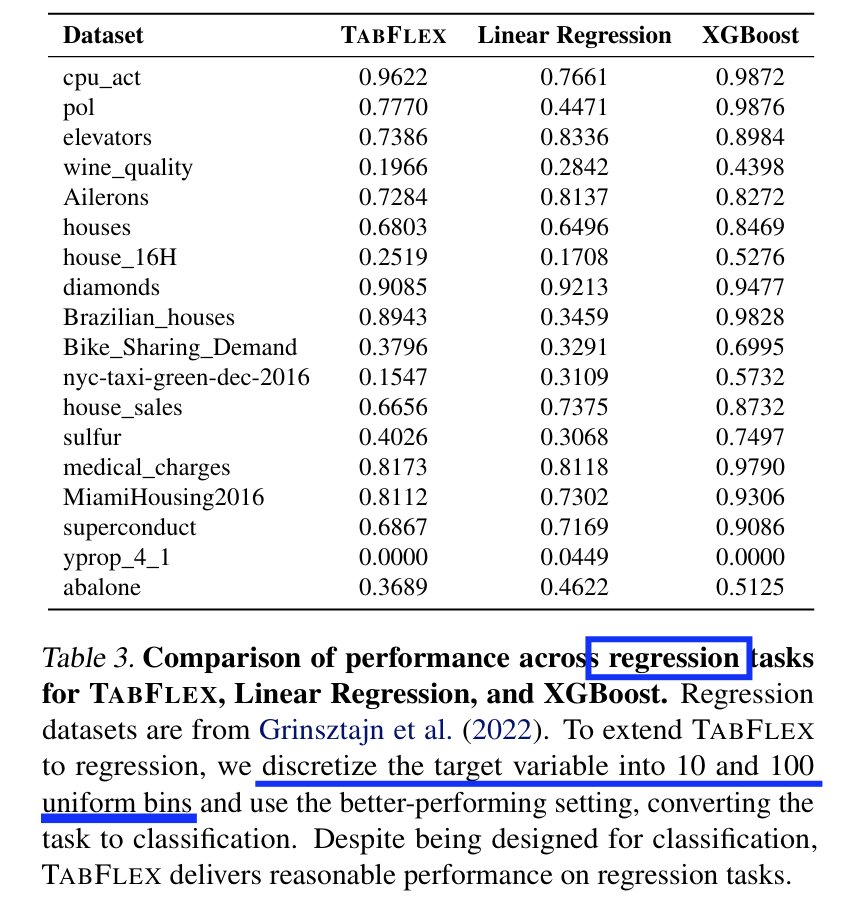
Findings: Reasonable performance (metric ??)

7. Ablation Studies

(1) Fine-Grained Comparison with XGBoost

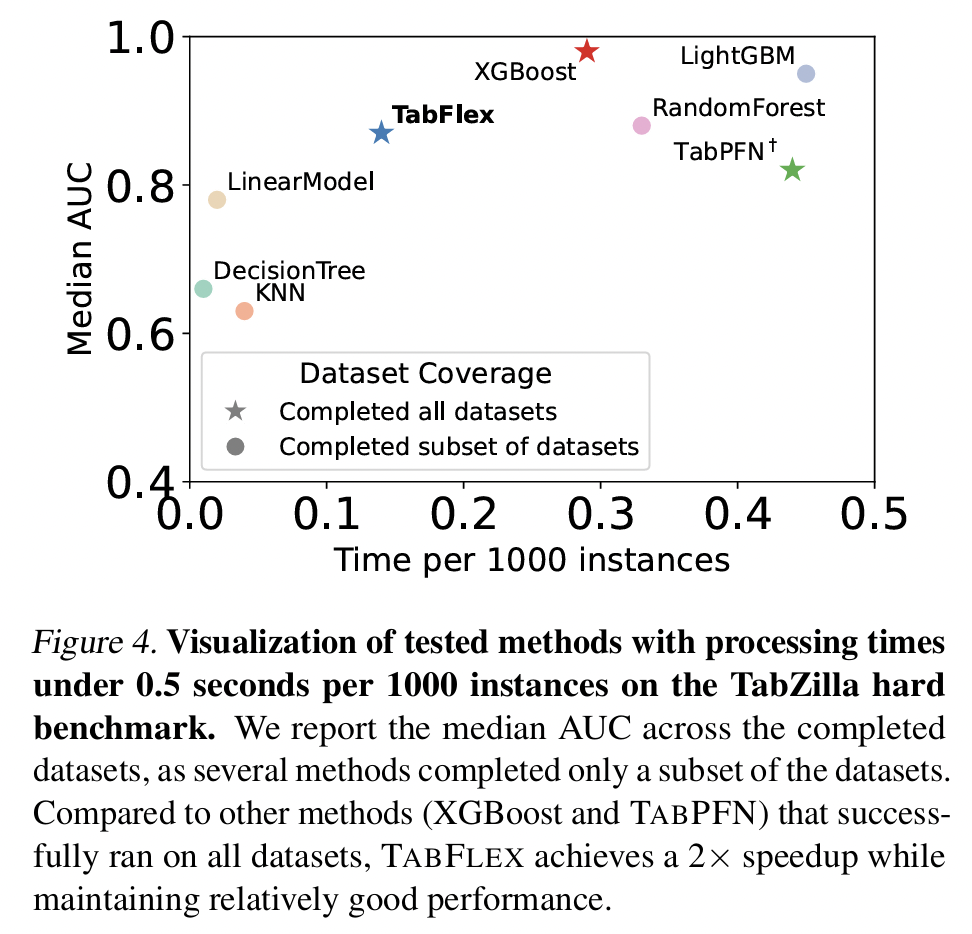
Larger performance gap between TabFlex & XGBoost

(Compared to the simpler datasets shown in Table 1)

\(\rightarrow\) WHY??

More fine-grained comparison using synthetic datasets!

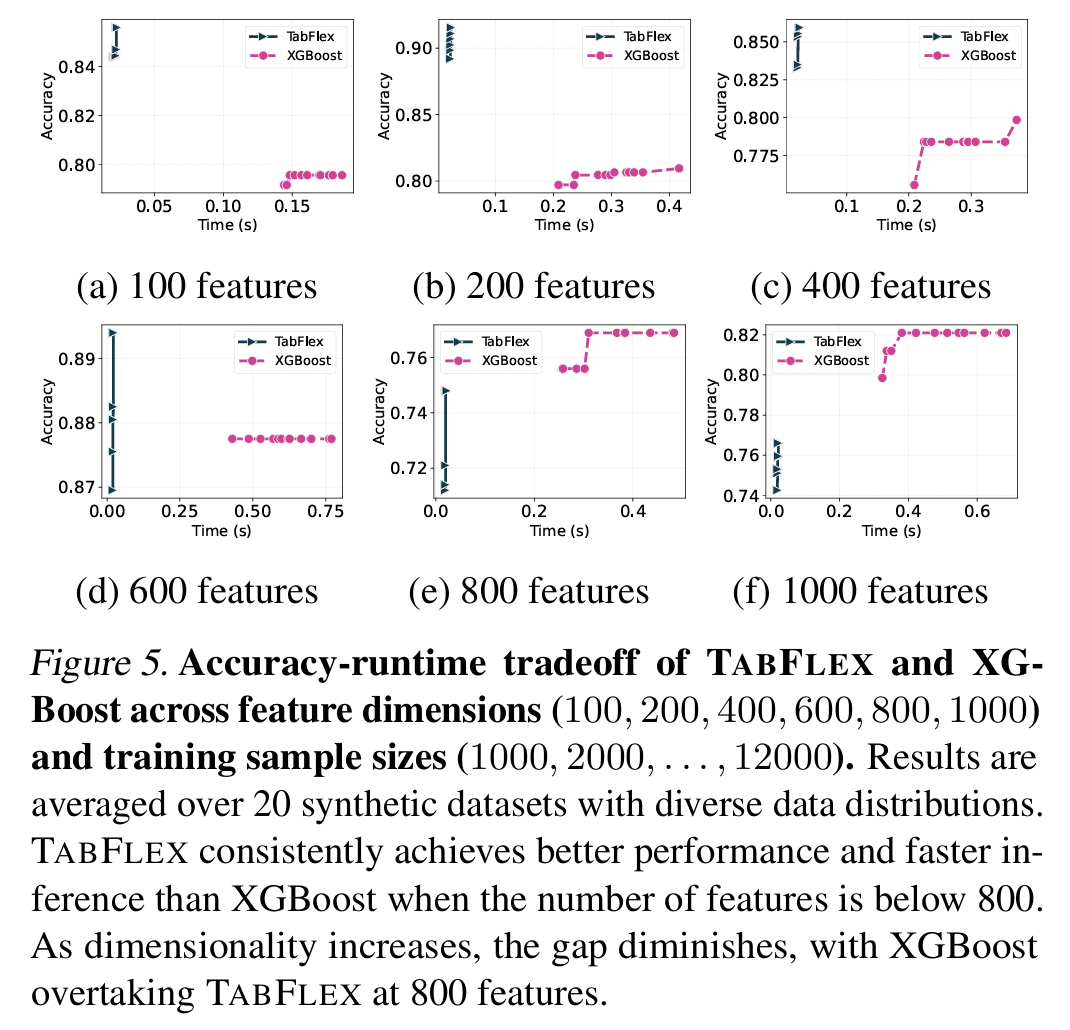
Findings

• TabFlex consistently outperforms XGBoost in both accuracy and inference time,

  when the feature dimensionality is below 800.

• As the number of features increases, the performance gap narrows, and XGBoost eventually surpasses TabFlex
• Nevertheless, TabFlex achieves a stronger overall tradeoff across most settings

(2) Incorporating Data-Efficient Techniques: Dimensionality Reduction and Data Sampling

TabFlex: Uilizes the ICL for prediction

\(\rightarrow\) \(\therefore\) Reducing the complexity of the data can further improve the inference efficiency!

Combine with two data-efficient techniques

• a) Dimensionality reduction
• b) Training data sampling

a) Dimensionality reduction

• Principal Components Analysis (PCA)
• Singular Value Decomposition (SVD)
• Random linear projection

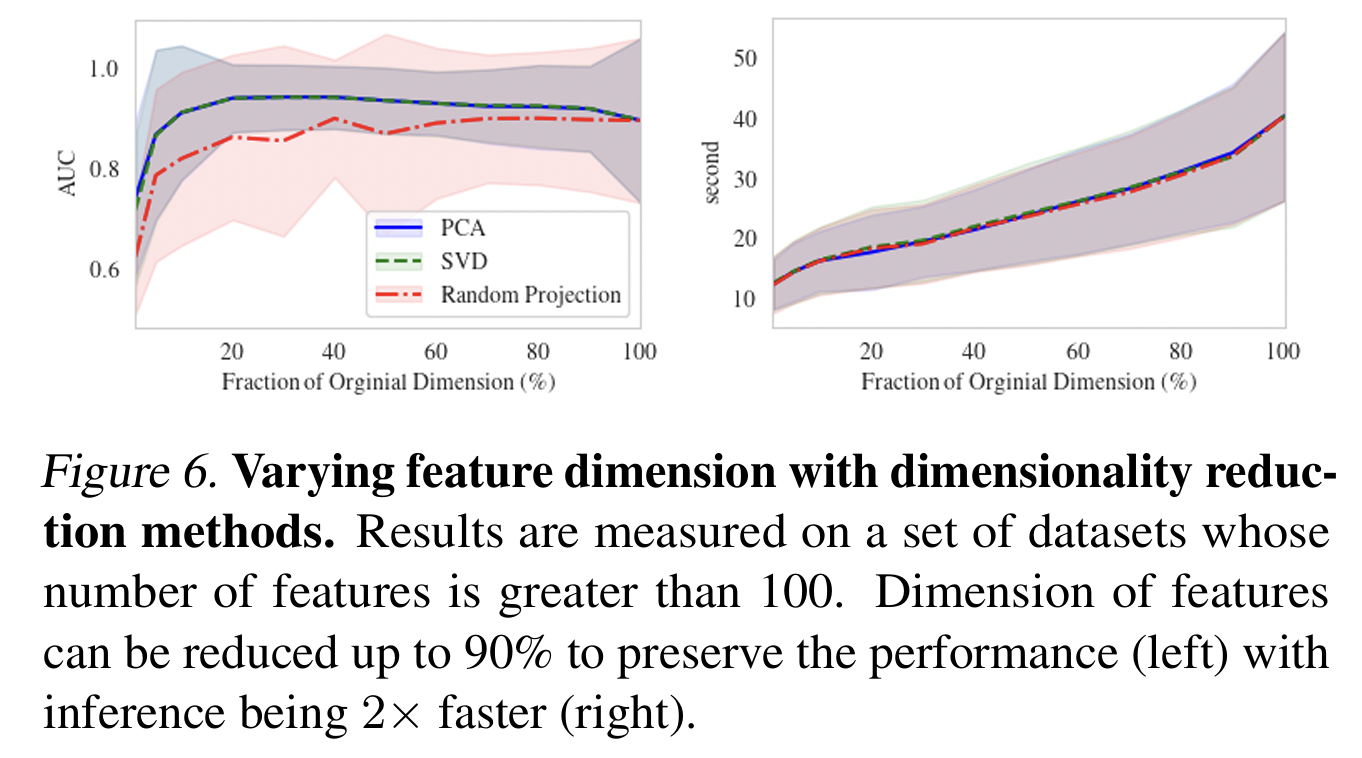
• Datasets: From Table 9 , with \(D>100\)

b) Training data sampling

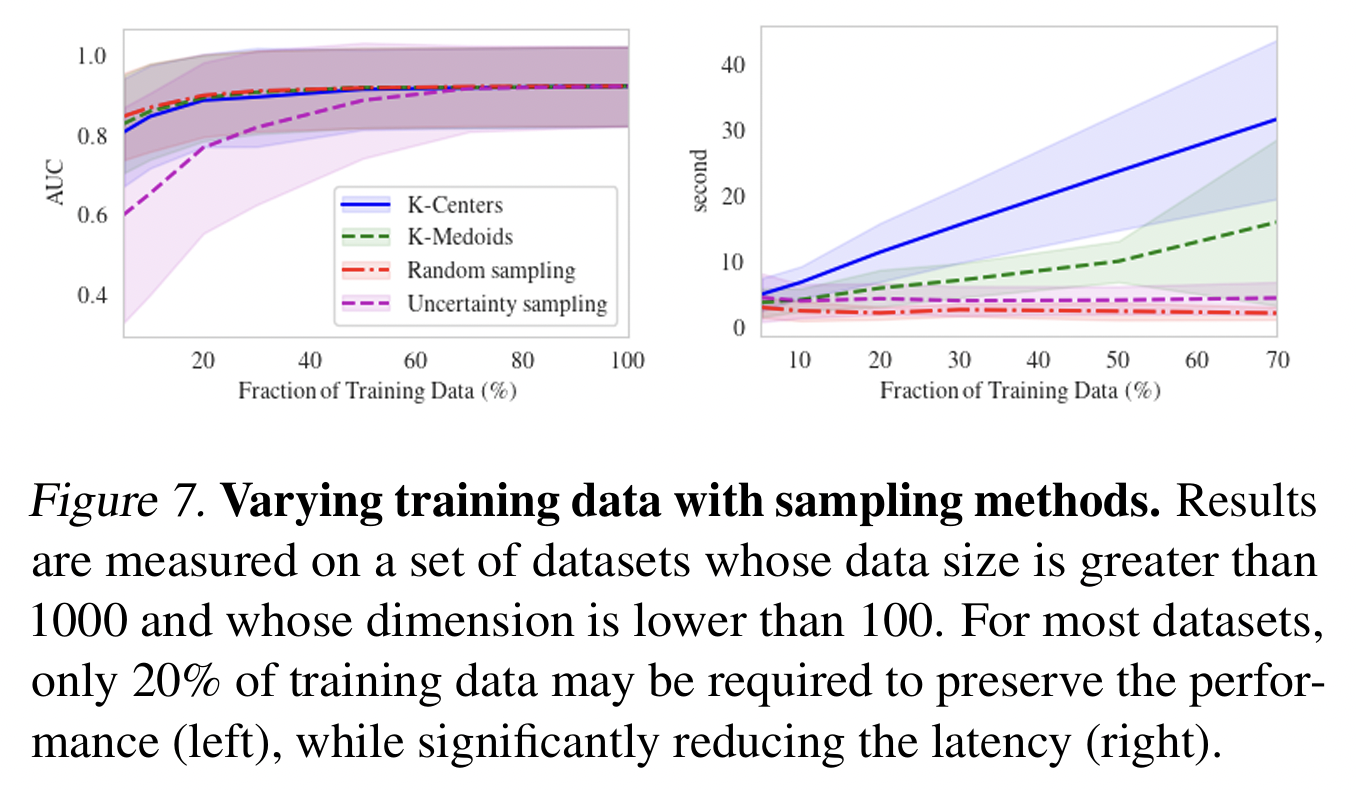
• Training data size with different sampling methods
  • e.g., K-centers, K-medoids, uncertainty sampling, and random sampling
• Datasets: From Table 9, with \(N>1000\) and \(D<100\)
• Findings:
  • Original performance can be preserved with only 20% of training data (while the latency can be significantly reduced)

8. Conclusion & Discussion

## (1) Conclusion

Comprehensive exploration of scalable alternatives to attention

\(\rightarrow\) Choose non-causal linear attention

(2) Limitations & Future Works

Current: Around 2K features

Future works: Scaling to even larger feature spaces!

Further extending TABFLEX to other modalities!

TabPFNv2 is a concurrent work that further improves the performance of TABPFN.

\(\rightarrow\) Investigating how incorporating linear attention might impact TabPFNv2 is also an interesting question for future research