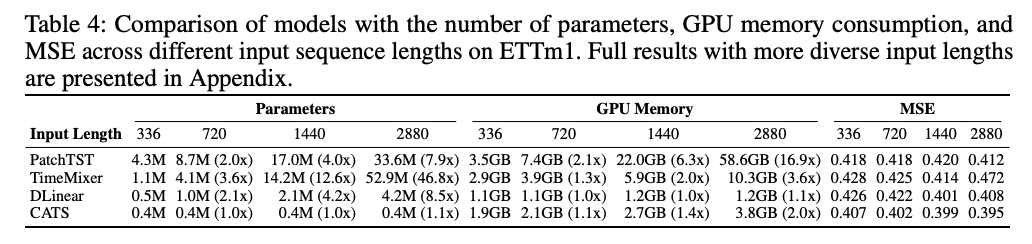
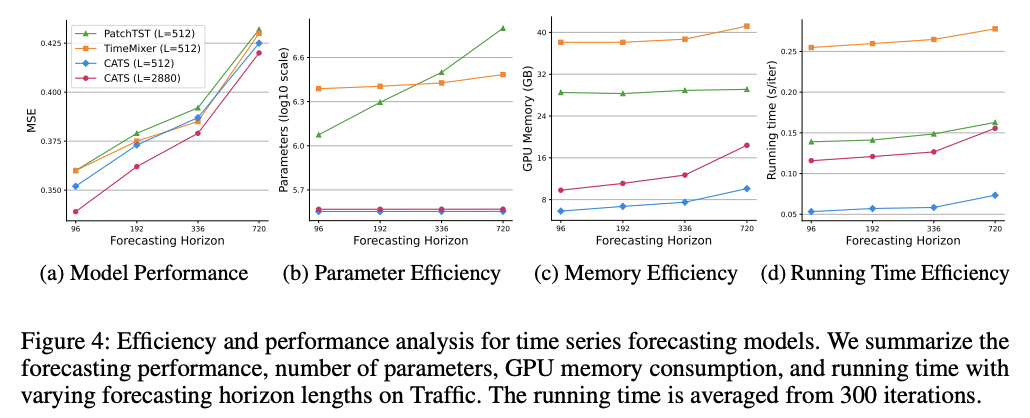
Are Self-Attentions Effective for TS Forecasting?

Are Self-Attentions Effective for TS Forecasting?

Contents

1. Abstract
2. Introduction
3. Temporal Information Encoding
4. Proposed Methodology
5. Experiments

0. Abstract

Transformer: effectiveness ??

This paper: Deals with Effectiveness of self-attentions for TS forecasting.

Cross-Attention-only TS Transformer (CATS)

• Self-attention (X) + Cross-attention (O)
• Establish future horizon dependent parameters as queries and enhanced parameter sharing,

1. Introduction

Are self-attentions effective for time series forecasting?

• (Previous works) [26]
  • limited to substituting attention layers with linear layers
• Previous issues: because of …
  • Self-attention (O)
  • Transformer (X)

\(\rightarrow\) Aim to solve the issues of self-attention

& Propose a new forecasting architecture that achieves higher performance with a more efficient structure

Cross-Attention-only Time Series transformer (CATS)

• Simplifies the original Transformer architecture

  • self-attentions (X)
  • cross-attentions (O)

• Establishes future horizon-dependent parameters as queries

  & Treats past TS data as key and value pairs

  \(\rightarrow\) Enhance parameter sharing & improve long-term forecasting performance.

2. Temporal information encoding

Zeng et al. [26]

• Argued that self-attention is not suitable for TS
• Due to its permutation invariant and anti-order properties
• Self-attnetion
  • Focus on building complex representations
  • Inefficient in maintaining the original context of historical and future values.
• Proposed linear models without any embedding layer

Time-index models ( Woo et al. [22] )

• Model the underlying dynamics with given time stamps

• Imply that preserving the order of TS sequences plays a crucial role in TS forecasting

3. Proposed Methodology

(1) Problem Definition and Notations

MTS forecasting task

• Prediction: \(\tilde{\boldsymbol{X}}=\left\{\mathbf{x}_{L+1}, \ldots, \mathbf{x}_{L+T}\right\} \in\) \(\mathbb{R}^{M \times T}\)
• Target: \(\hat{\boldsymbol{X}}=\left\{\hat{\mathbf{x}}_{L+1}, \ldots, \hat{\mathbf{x}}_{L+T}\right\} \in \mathbb{R}^{M \times T}\)
• Input: \(\boldsymbol{X}=\) \(\left\{\mathbf{x}_1, \ldots, \mathbf{x}_L\right\} \in \mathbb{R}^{M \times L}\).

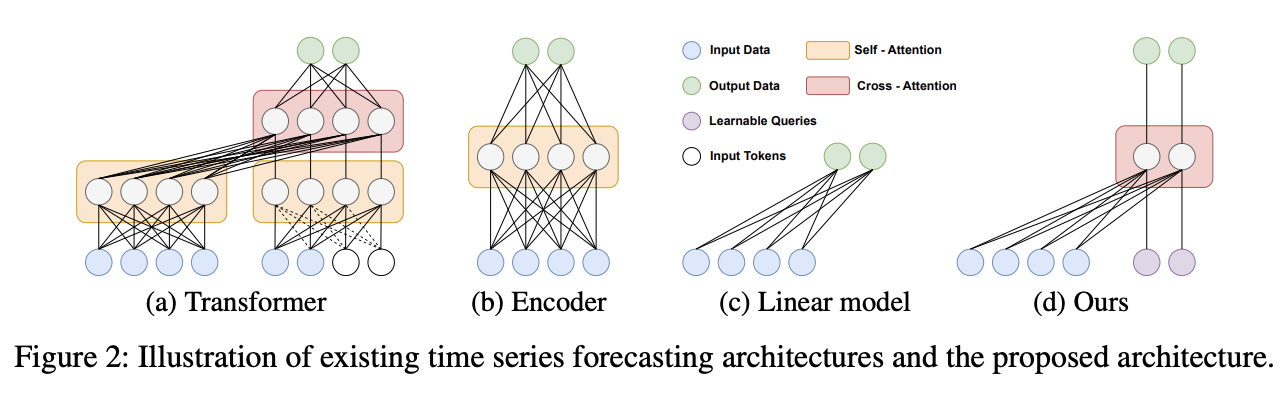
Traditional TS transformers

• Step 1) Embeddding \(\boldsymbol{X}\) to \(\boldsymbol{H}_L \in \mathbb{R}^{D \times L}\)
  • (case1: CI) Considered to separate UTS \(\mathbf{x} \in \mathbb{R}^{1 \times L}\).
  • (case2: Patching) Transforms into patches \(\mathbf{p}=\) \(\operatorname{Patch}(\mathbf{x}) \in \mathbb{R}^{P \times N_L}\)
    • \(\boldsymbol{H}_L=\operatorname{Embedding}(\mathbf{p}) \in \mathbb{R}^{D \times N_L}\).

Notation

• Self-Attention (SA)
• Masked Self-Attention (MSA)
• Cross-Attention (CA)
• LayerNorm (LN)

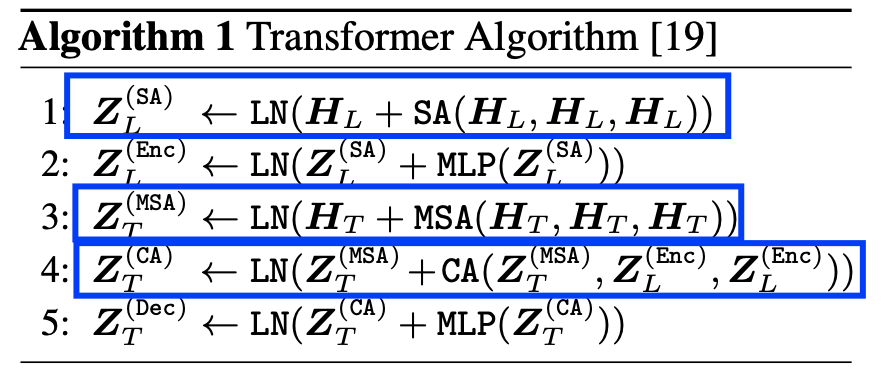
For input tokens \(\boldsymbol{H}_T\) for cross-attention…,

• Positional embedding is often used

Output from the cross-attention, \(\boldsymbol{Z}_T^{(\mathrm{Dec})} \in \mathbb{R}^{D \times N_T}\), is subsequently used to produce the final prediction \(\hat{\boldsymbol{X}}\) through additional layers.

( If no decoder = Encoder-only models (Fig 2b) )

(2) Model Structure

Summary

• Not only preserves the temporal information

• But also utilizes the structural advantages of the Transformer

[Figure 2d]

• Cross-attention Transformer
  • Maintain the periodic properties of TS
  • ( not for self-attention, which has permutation-invariant and anti-order characteristics )
• Replacing with Linear layer??
  • Potential of the transformer architecture itself (excluding self-attention) has been overlooked.

Introduce a novel approach!

\(\rightarrow\) Cross-attention without self-attention

Consists of three key components:

• (A) Cross-Attention with Future as Query
• (B) Parameter Sharing across Horizons
• (C) Query-Adaptive Masking

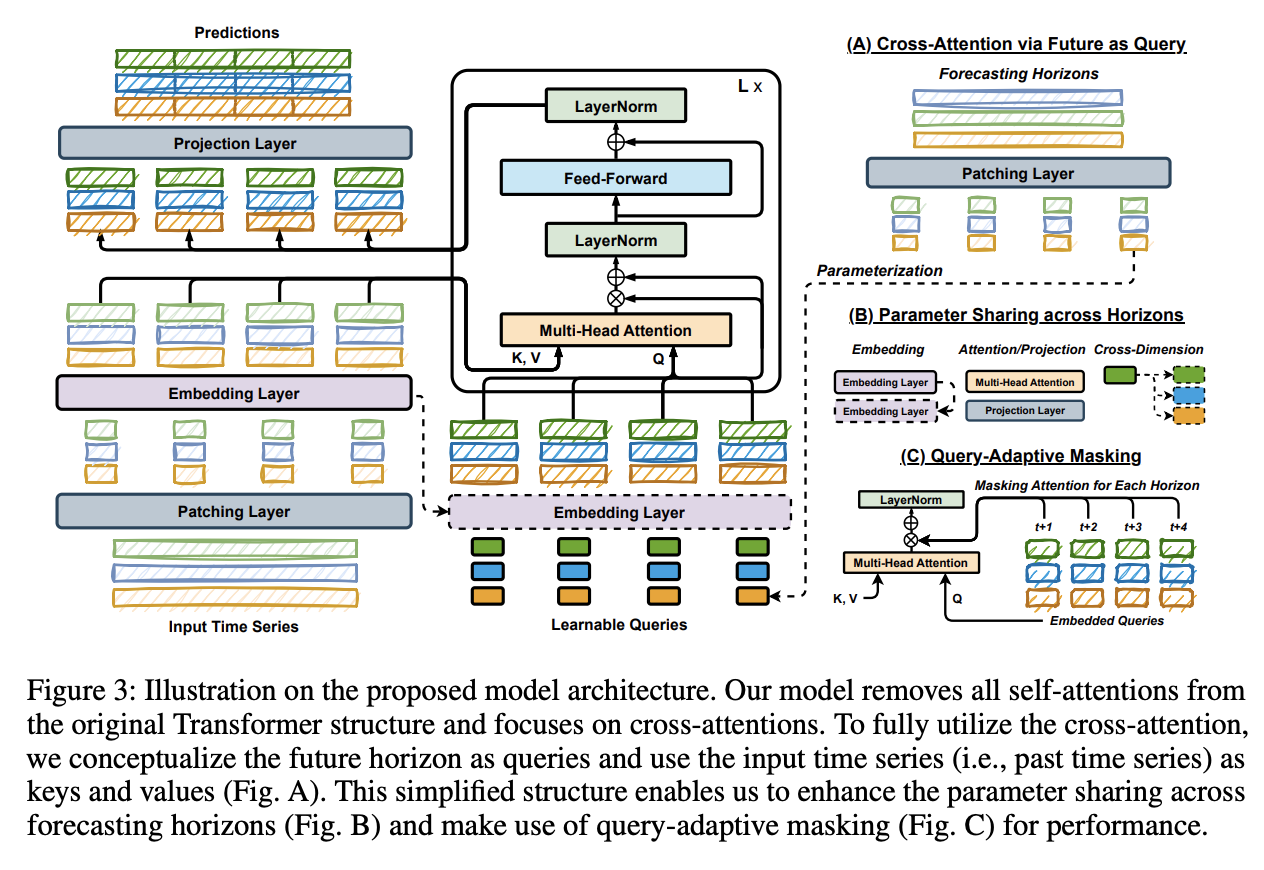
Details

• Remove self-attention & Incorporate cross-attention

  ( + Utilize future data as the query )

• Simplify the architecture by parameter sharing across forecasting horizons.

• Enhance the performance through query-adaptive masking

a) Cross-Attention via Future as Query

Cross-attention mechanism:

• Query: From a different source than the key or value

\(\rightarrow\) Argue that each future horizon should be regarded as a question, i.e., an independent query.

Horizon-dependent parameters (as learnable queries)

Step 1) Create parameters ( = learnable queries \(\mathbf{q} \in \mathbb{R}^P\). )

• For the specified forecasting horizon
  • ex) \(\mathbf{q}_i\) : Horizon-dependent query at \(L+i\).

Step 2) Utilize a cross-attention-only structure in the decoder

• Resulting in an advantage in efficiency.

• DECODER-only model

b) Parameter Sharing across Horizons

Strongest benefits of cross-attention via future horizon as a query \(\mathbf{q}\):

• CA is only calculated on the values from a single forecasting horizon and the input TS

Independent forecasting mechanism : Prediction \(\hat{\mathbf{x}}_{L+i}\) is …

• Depenent on the past samples \(\boldsymbol{X}=\left[\mathbf{x}_1, \ldots, \mathbf{x}_L\right]\) and \(\mathbf{q}_i\)

  & Independent of \(\mathbf{q}_j\) for all \(i \neq j\)

• Notable advantage: a higher level of parameter sharing

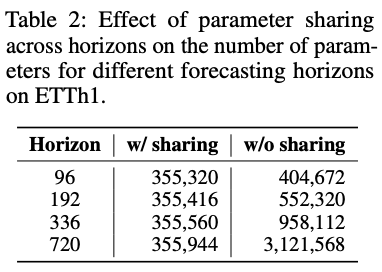
Propose parameter sharing across all possible layers

• Embedding layer
• Multi-head attention

• Projection layer

  for every horizon-dependent query \(\mathbf{q}\)

In other words….

• All horizon queries \(\mathbf{q}_1, \ldots, \mathbf{q}_T\) (or \(\mathbf{q}_1, \ldots, \mathbf{q}_{N_T}\) )
• share the same embedding layer
• used for the input TS \(\mathbf{x}_1, \ldots, \mathbf{x}_L\) (or patches \(\mathbf{p}_1, \ldots, \mathbf{p}_{N_L}\) )
• before proceeding to the cross-attention layer

To maximize the parameter sharing,

also propose cross-dimension sharing

• use the same query parameters for all dimensions.

Projection (prediction) Layer:

• Share the projection layer for each prediction.

  • PatchTST: FC layer as the projection layer
    • for the concatenated outputs \(\boldsymbol{Z}_T^{(\text {Dec) }}\).
    • # of params: \(\left(D \times N_L\right) \times T\).

  • CATS: shares the same projection layer for each prediction.

    • # of params: \(D \times P\),

      ( not proportionally increasing to \(T\). )

c) Query-Adaptive Masking

[Limitation]

High degree of parameter sharing: could lead to…

• overfitting to the keys and values (i.e., past time series data),
• rather than the queries (i.e., forecasting horizon).

[Solution]

To ensure the model focuses on each horizon-dependent query \(\mathbf{q}\)

\(\rightarrow\) Introduce a new technique that masks the attention outputs

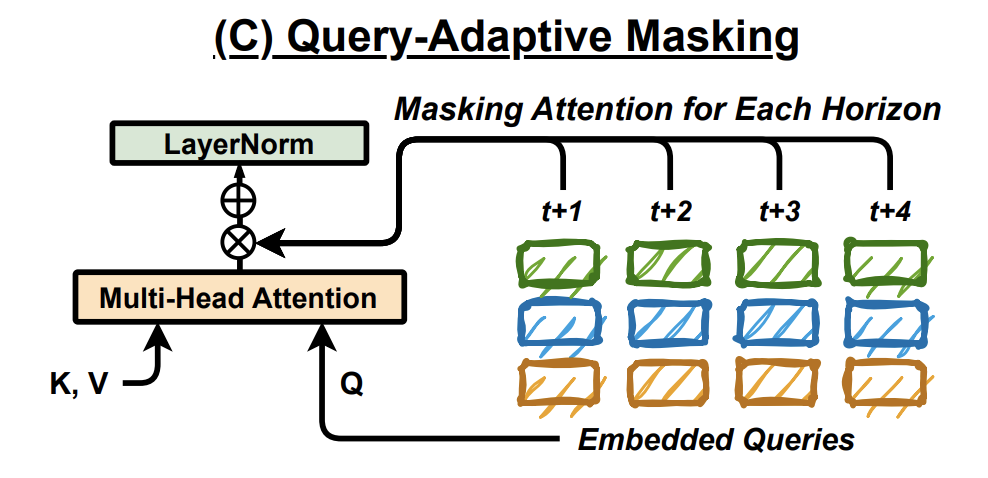
• For each horizon, we apply a mask to the direct connection from Multi-Head Attention to LayerNorm with a probability \(p\).

• Result: Prevents access to the input TS

  \(\rightarrow\) Resulting in only the query to influence prediction

• Helps the layers to concentrate more effectively on the forecasting queries.

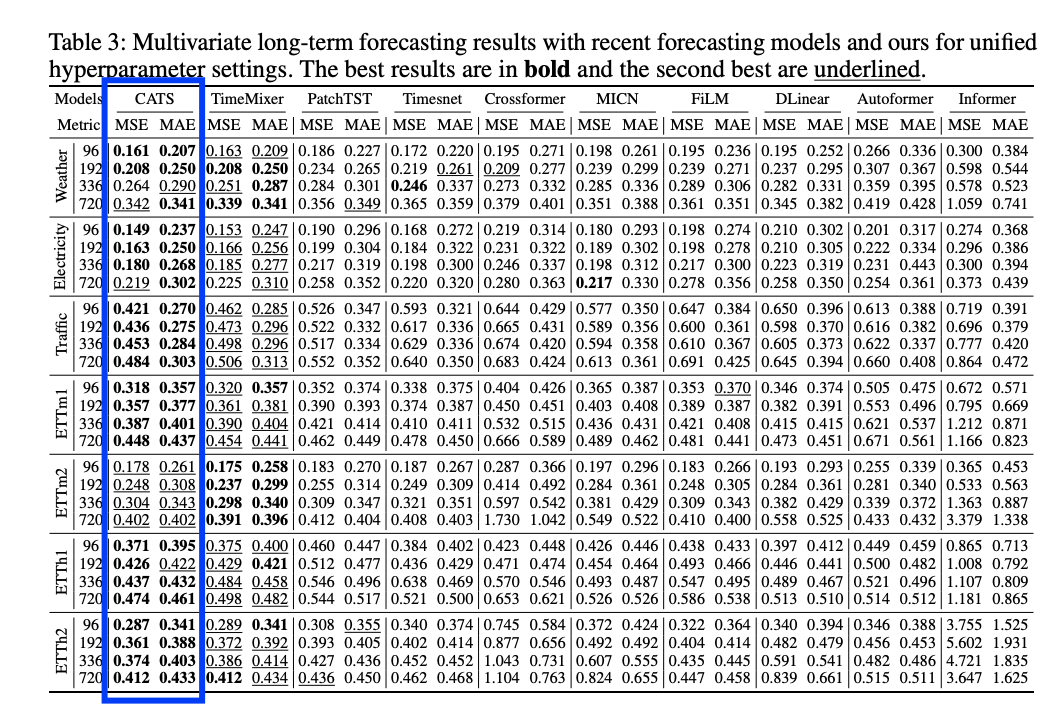
4. Experiments

(1) LTSF

(2) Efficiency & Robust Forecasting for Long Input Sequences