Dance of Channel And Sequence; AN Efficient Attention-based Approach for MTS Forecasting

Dance of Channel And Sequence: AN Efficient Attention-based Approach for MTS Forecasting

Contents

1. Abstract
2. Introduction
3. Related Works
   1. CI Models
   2. CD Models
4. CSFormer
   1. Preliminaries
   2. Dimension-augmented Embedding
   3. Two-stage MSA
   4. Prediction

0. Abstract

It is imperative to acknowledge the intricate interplay among channels

\(\rightarrow\) CI: impractical, leading to information degradation

CSformer

1. Two-stage self-attention mechanism.

• Enable the segregated extraction of

  • (1) sequence-specific
  • (2) channel-specific

  information, while sharing parameters btw sequences and channels.

1. Sequence adapters & Channel adapters

1. Introduction

[CI] PatchTST (Nie et al., 2023)

[CD] TSMixer (Ekambaram et al., 2023), Crossformer (Zhang & Yan, 2023)

• Fall short in capturing the mutual information between sequence and channel information
• Information distortion during data processing

CSformer

• Efficiently extracts and interplays sequence and channel information
• no change to attention in Transformer

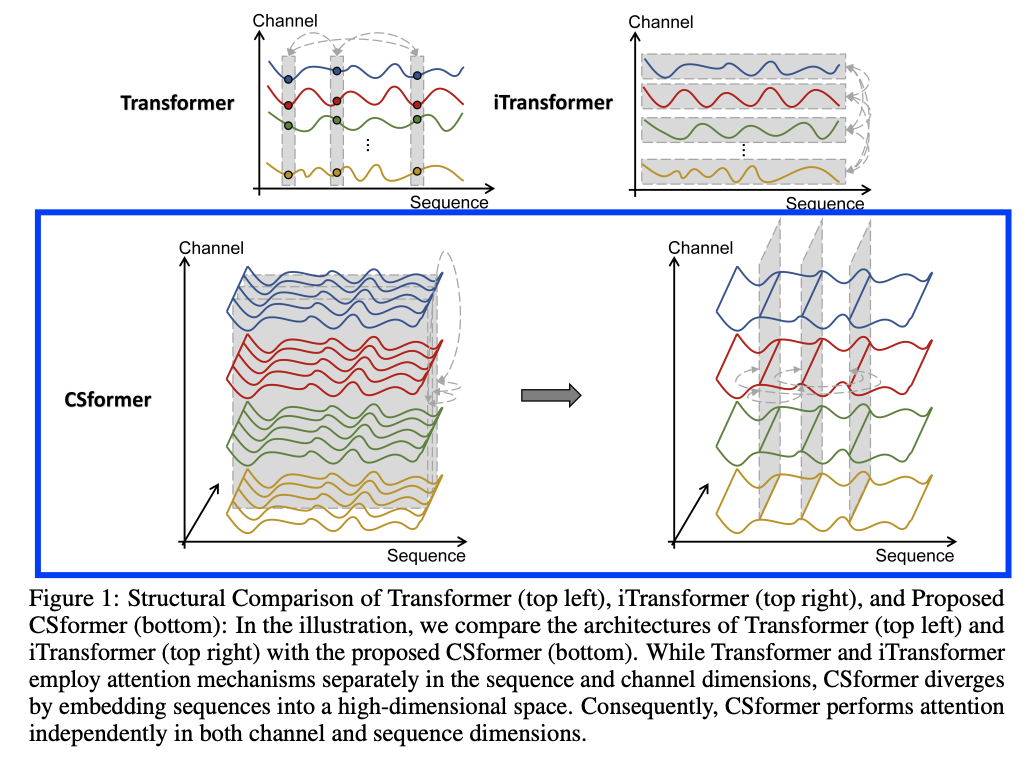
• (1) Dimensionality-augmented embedding
  • Elevates the dimensionality of sequences without compromising the integrity of the original information.
• (2) Shared attention mechanism
  • along the sequence and channel dimensions
  • share parameters, facilitating mutual influence
• (3) Adapter
  • Sequence adapters
  • Channel adapters

2. Related Works

(1) CI models

• DLinear
• PatchTST

(2) CD models

• Crossformer
• TSMixer
• iTransformer

PatchTST (Nie et al., 2023)

• extracting cross-dependency in an inappropriate manner would introduce noises

Motivation for CSformer

\(\rightarrow\) Find an effective way to leverage cross-variable information while adequately extract temporal information simultaneously.

3. CSFormer

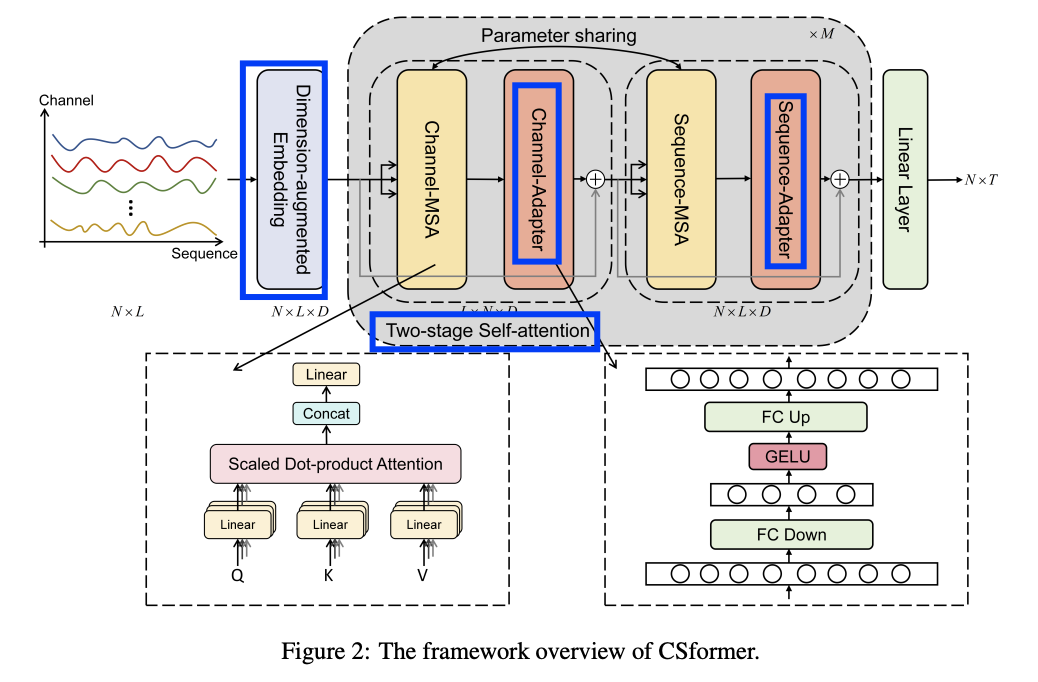
Capable of concurrently learning channel and sequence information.

• Step 1) Dimension-augmented Embedding
• Step 2) Two-stage attention mechanism
  • For channel & sequence
  • Share parameters, facilitating interaction between channel and sequence information
• Step 3) Channel & Sequence adapters
  • To ensure the distinct roles

(1) Preliminaries

Input TS: \(\mathbf{X}=\left\{\mathbf{x}_1, \ldots, \mathbf{x}_L\right\} \in \mathbb{R}^{N \times L}\),

• \(\mathbf{x}_i \in \mathbb{R}^N\) : variables at the \(i\)-th time point
• \(\mathbf{X}^{(k)} \in \mathbb{R}^L\) : sequence of the \(k\)-th variable

Prediction: \(\hat{\mathbf{X}}=\left\{\mathbf{x}_{L+1}, \ldots, \mathbf{x}_{L+T}\right\} \in \mathbb{R}^{N \times T}\).

Model: \(\mathbf{f}_\theta\)

MTS forecasting: \(\mathbf{f}_\theta(\mathbf{X}) \rightarrow \hat{\mathbf{X}}\).

(2) Dimension-augmented Embedding

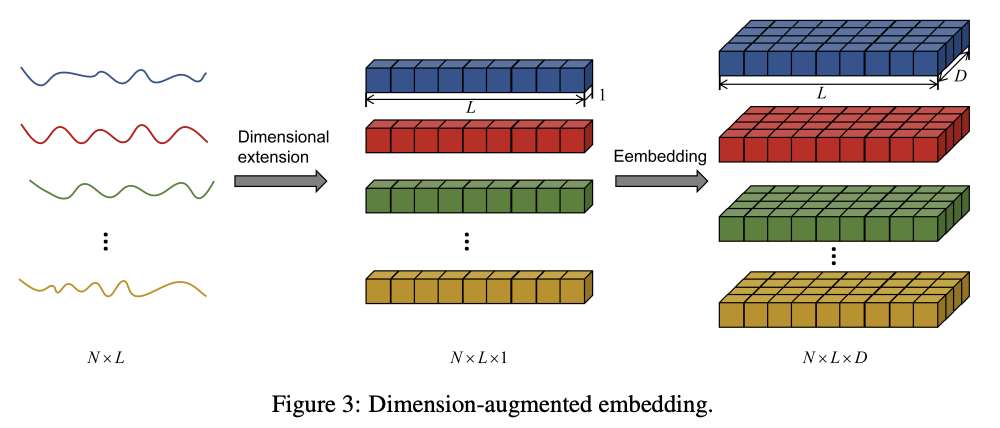
Uplift Embedding

• \(\mathbf{X} \in \mathbb{R}^{N \times L} \rightarrow \mathbf{X} \in \mathbb{R}^{N \times L \times 1}\).
• \(\mathbf{H} \in \mathbb{R}^{N \times L \times D}=\mathbf{X} \times \nu\).
  • Learnable vector \(\nu \in \mathbb{R}^{1 \times D}\),

(3) Two-stage MSA

Consisting of \(M\) blocks

• Each block = Two stage MSA.

Following the output of each MSA,

\(\rightarrow\) Adapter is appended !

Adapter

• Ensure discriminative learning of channel and sequence information
• Comprises two fully connected layers and an activation function layer

a) Channel MSA

Channel-wise attention at each time step to discern inter-channel dependencies

\(\mathbf{Z}_c=\operatorname{MSA}\left(\mathbf{H}_c\right)\),

• where \(\mathbf{H}_c \in \mathbb{R}^{L \times N \times D}\) , \(\mathbf{Z}_c \in \mathbb{R}^{L \times N \times D}\)

\(\mathbf{A}_c=\operatorname{Adapter}\left(\operatorname{Norm}\left(\mathbf{Z}_c\right)\right)+\mathbf{H}_c\).

• where \(\mathbf{A}_c \in \mathbb{R}^{L \times N \times D}\)

b) Sequence MSA

Reshape operation to seamlessly transition into \(\mathbf{H}_s\)

\(\mathbf{Z}_s=\operatorname{MSA}\left(\mathbf{H}_s\right)\).

• where \(\mathbf{H}_s \in \mathbb{R}^{N \times L \times D}\), \(\mathbf{Z}_s \in \mathbb{R}^{N \times L \times D}\)

\(\mathbf{A}_s=\operatorname{Adapter}\left(\operatorname{Norm}\left(\mathbf{Z}_s\right)\right)+\mathbf{H}_s\),

• where \(\mathbf{A}_s \in \mathbb{R}^{N \times L \times D}\)

(4) Prediction

Reshaping: resulting in \(\mathbf{Z} \in \mathbb{R}^{N \times(L * D)}\).

With linear layer: \(\hat{\mathbf{X}} \in \mathbb{R}^{N \times T}\).