Seunghan Lee

Seunghan Lee

Deep Learning, Data Science, Statistics

ContiFormer: Continuous-Time Transformer for Irregular Time Series Modeling


Contents

  1. Abstract
  2. Preliminaries
  3. Methodology
    1. Overview
    2. Embedding Layer
    3. Mamba Pre-processing Layer
    4. MambaFormer Layer
    5. Forecasting Layer
  4. Experiments


0. Abstract

Continuous-time dynamics on Irregular TS (ITS)

  • critical to account for (1) data evolution and (2) correlations that occur continuously


Previous works

  • a) RNN, Transformer models: discrete

    $\rightarrow$ Limitations in generalizing to continuous-time data paradigms.

  • b) Neural ODEs

    • Promising results in dealing with ITS
    • Fail to capture the intricate correlations within these sequences


ContiFormer

  • Extends the relation modeling of Transformer to the continuous-time domain
  • Explicitly incorporates the modeling abilities of continuous dynamics of Neural ODEs with the attention mechanism of Transformers.


1. Introduction

Paragraph 1) Characteristics of ITS

  • (1) Irregularly generated or non-uniformly sampled observations with variable time intervals
  • (2) Still, the underlying data-generating process is assumed to be continuous
  • (3) Relationships among the observations can be intricate and continuously evolving.


Paragraph 2) Challenges for moddel design

  • Divide into equally sized intervals??

$\rightarrow$ Weverely damage the continuity of the data

  • Recent works)
    • Underlying continuous-time process is appreciated for ITS modeling
  • Argue that the correlation within the observed data is also constantly changing over time


Paragraph 3) Two main branches

  • (1) Neural ODEs & SSMs
    • Pros) Promising abilities for capturing the dynamic change of the system over time
    • Cons) Overlook the intricate relationship between observations
  • (2) RNN & Transformers
    • Pros) Capitalizes on the powerful inductive bias of NN
    • Cons) Fixed-time encoding or learning upon certain kernel functions … fails to capture the complicated input-dependent dynamic systems


Paragraph 4) ContiFormer (Continuous-Time Transformer)

  • ContiFormer = (a) + (b)

    • (a) Continuous dynamics of Neural ODEs
    • (b) Attention mechanism of Transformers

    $\rightarrow$ Breaks the discrete nature of Transformer models.

  • Process

    • Step 1) Defining latent trajectories for each observation in the given irregularly sampled data points
    • Step 2) Extends the “discrete” dot-product in Transformers to a “continuous”-time domain
      • Attention: calculated between continuous dynamics.


Contribution

a) Continuous-Time Transformer

  • First to incorporate a continuous-time mechanism into attention calculation in Transformer,

b) Parallelism Modeling

  • Propose a novel reparameterization method, allowing us to parallelly execute the continuous-time attention in the different time ranges

c) Theoretical Analysis

  • Mathematically characterize that various Transformer variants can be viewed as special instances of ContiFormer

d) Experiment Results

  • TS interpolation, classification, and prediction


2. Method

Irregular TS

  • $\Gamma=\left[\left(X_1, t_1\right), \ldots,\left(X_N, t_N\right)\right]$,
    • Observations may occur at any time
    • Observation time points $\boldsymbol{\omega}=\left(t_1, \ldots, t_N\right)$ are with irregular intervals
  • $X=\left[X_1 ; X_2 ; \ldots, X_N\right] \in \mathbb{R}^{N \times d}$.


figure2


Input)

  • (1) Irregular time series $X$
  • (2) Sampled time $\boldsymbol{\omega}$
    • Sequence of (reference) time points
    • $t$ : random variable representing a query time point

Output)

  • Latent continuous trajectory

    ( = captures the dynamic change of the underlying system )


Summary

  • Transforms the discrete observation sequence into the continuous-time domain
  • Attention module ( = Continuous perspective )
    • Expands the dot-product operation in vanilla Transformer to the continuous-time domain
      • (1) Models the underlying continuous dynamics
      • (2) Captures the evolving input-dependent process


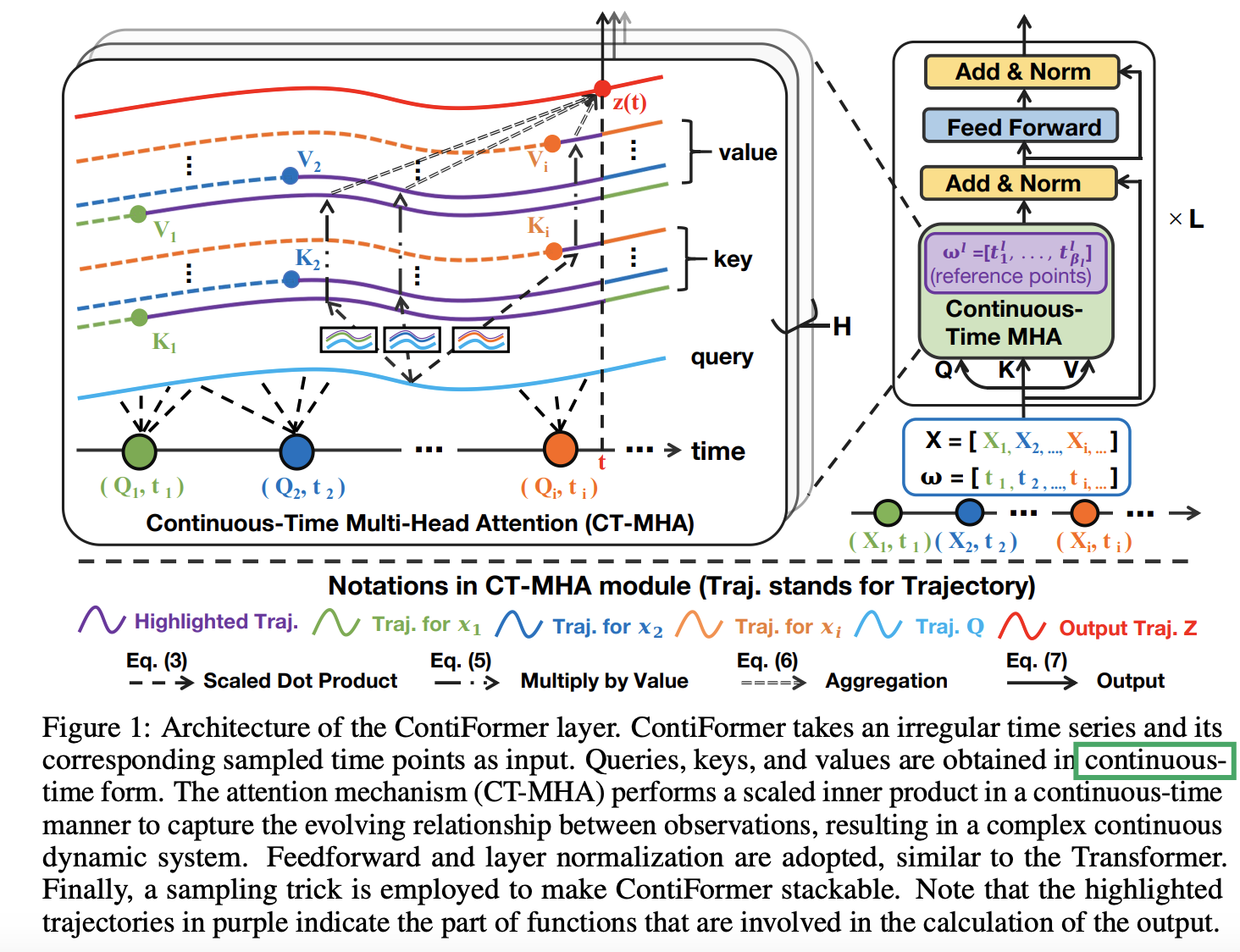
(1) Continuous-Time Attention Mechanism

Core of the ContiFormer layer

  • continuous-time multi-head attention (CT-MHA)
  • Transform $X$ into…
    • $Q=\left[Q_1 ; Q_2 ; \ldots ; Q_N\right]$,
    • $K=\left[K_1 ; K_2 ; \ldots ; K_N\right]$,
    • $V=\left[V_1 ; V_2 ; \ldots ; V_N\right]$.
  • Utilize ODE to define the latent trajectories for each observation.
    • Latent space: assume that the underlying dynamics evolve following linear ODEs
  • Construct a continuous query function
    • by approximating the underlying sample process of the input.


a) Continuous Dynamics from Observations

Attention in continuous form

Step 1) Empoy ODE to define the latent trajectories for each observation

  • ex) first observation: at time point $t_1$
  • ex) last observation: at time point $t_N$

Continuous keys and values:

  • $\mathbf{k}_i\left(t_i\right)=K_i$,
    • $ \mathbf{k}i(t)=\mathbf{k}_i\left(t_i\right)+\int{t_i}^t f\left(\tau, \mathbf{k}_i(\tau) ; \theta_k\right) \mathrm{d} \tau$.
  • $\mathbf{v}_i\left(t_i\right)=V_i$
    • $ \mathbf{v}i(t)=\mathbf{v}_i\left(t_i\right)+\int{t_i}^t f\left(\tau, \mathbf{v}_i(\tau) ; \theta_v\right) \mathrm{d} \tau$.

Notation:

  • $t \in\left[t_1, t_N\right], \mathbf{k}_i(\cdot), \mathbf{v}_i(\cdot) \in \mathbb{R}^d$:
    • Represent the ODE for the $i$-th observation
      • with parameters $\theta_k$ and $\theta_v$,
      • with initial state of $\mathbf{k}_i\left(t_i\right)$ and $\mathbf{v}_i\left(t_i\right)$
  • $f(\cdot) \in \mathbb{R}^{d+1} \rightarrow \mathbb{R}^d$:
    • Controls the change of the dynamics


b) Query Function

To model a dynamic system, queries can be modeled as a function of time

  • Represents the overall changes in the input

Adopt a common assumption that irregular time series is a “discretization” of an underlying continuous-time process

$\rightarrow$ Define a closed-form continuous-time interpolation function (e.g., natural cubic spline) with knots at $t_1, \ldots, t_N$ such that $\mathbf{q}\left(t_i\right)=Q_i$ as an approximation of the underlying process.


c) Scaled Dot Product

Self-attention

  • Calculating the correlation between queries and keys

  • By inner product ( $Q \cdot K^{\top}$ )


Extending the **discrete ** inner-product to its **continuous-time ** domain!!

  • Two real functions: $f(x)$ and $g(x)$
  • Inner product of two functions in a closed interval $[a, b]$ :
    • $\langle f, g\rangle=\int_a^b f(x) \cdot g(x) \mathrm{d} x$.
    • Meaning = How much the two functions “align” with each other over the interval


$\boldsymbol{\alpha}i(t)=\frac{\int{t_i}^t \mathbf{q}(\tau) \cdot \mathbf{k}_i(\tau)^{\top} \mathrm{d} \tau}{t-t_i}$.

Evolving relationship between the..

  • (1) “$i$-th sample” (key)
  • (2) “dynamic system” at time point $t$ (query)
  • in a closed interval $\left[t_i, t\right]$,

$\rightarrow$ To avoid numeric instability during training, we divide the integrated solution by the time difference


Discontinuity at $\boldsymbol{\alpha}_i\left(t_i\right)$…. How to solve?

Define $\boldsymbol{\alpha}_i\left(t_i\right)$ as …

$\boldsymbol{\alpha}i\left(t_i\right)=\lim _{\epsilon \rightarrow 0} \frac{\int{t_i}^{t_i+\epsilon} \mathbf{q}(\tau) \cdot \mathbf{k}_i(\tau)^{\top} \mathbf{d} \tau}{\epsilon}=\mathbf{q}\left(t_i\right) \cdot \mathbf{k}_i\left(t_i\right)^{\top}$.


d) Expected Values

Query time $t \in\left[t_1, t_N\right]$,

Value of an observation at time point $t$: expected value from $t_i$ to $t$

= $\widehat{\mathbf{v}}i(t)=\mathbb{E}{t \sim\left[t_i, t\right]}\left[\mathbf{v}i(t)\right]=\frac{\int{t_i}^t \mathbf{v}_i(\tau) \mathrm{d} \tau}{t-t_i}$


e) Multi-Head Attention

Summary

  • Allows for the modeling of complex, time-varying relationships between keys, queries, and values

  • Allows for a more fine-grained analysis of data by modeling the input as a continuous function of time

Continuous-time attention ( given a query time $t$ )

$\begin{aligned} \operatorname{CT}-\operatorname{ATTN}(Q, K, V, \boldsymbol{\omega})(t) & =\sum_{i=1}^N \widehat{\boldsymbol{\alpha}}i(t) \cdot \widehat{\mathbf{v}}_i(t)
\text { where } \widehat{\boldsymbol{\alpha}}_i(t) & =\frac{\exp \left(\boldsymbol{\alpha}_i(t) / \sqrt{d_k}\right)}{\sum{j=1}^N \exp \left(\boldsymbol{\alpha}_j(t) / \sqrt{d_k}\right)} \end{aligned}$.


Simultaneous focus on different input aspects

Stabilizes training by reducing attention weight variance


Multi-head: $\operatorname{CT}-\operatorname{MHA}(Q, K, V, \boldsymbol{\omega})(t)=\operatorname{Concat}\left(\operatorname{head}{(1)}(t), \ldots, \operatorname{head}{(\mathrm{H})}(t)\right) W^O$.


(2) Continuous-Time Transformer

$\begin{aligned} & \tilde{\mathbf{z}}^l(t)=\mathrm{LN}\left(\operatorname{CT}-\operatorname{MHA}\left(X^l, X^l, X^l, \omega^l\right)(t)+\mathbf{x}^l(t)\right)
& \mathbf{z}^l(t)=\operatorname{LN}\left(\operatorname{FFN}\left(\tilde{\mathbf{z}}^l(t)\right)+\tilde{\mathbf{z}}^l(t)\right) \end{aligned}$.


a) Sampling Process

ContiFormer layer

  • Output: Continuous function $\mathbf{z}^l(t)$ w.r.t. time as the output
  • Input: Discrete sequence $X^l$


How to incorporate $\mathbf{z}^l(t)$ into NN?

$\rightarrow$ Establish reference time points for the output of each layer


Reference time points

  • Used to discretize the layer output
  • Correspond to either
    • Input time points (i.e., $\boldsymbol{\omega}$ )
    • Task-specific time points.

Assume that the reference points for the $l$-th layer is $\boldsymbol{\omega}^l=\left[t_1^l, t_2^l, \ldots, t_{\beta_l}^l\right]$,

$\rightarrow$ Input to the next layer $X^{l+1}$ : sampled as $\left{\mathbf{z}^l\left(t_j^l\right) \mid j \in\left[1, \beta_l\right]\right}$

Categories:

Updated:

You May Also Enjoy

3 minute read

6 minute read

4 minute read

less than 1 minute read