Frequency Adaptive Normalization For Non-stationary Time Series Forecasting
Contents
- Abstract
- Introduction
-
FAN
- Experiments
0. Abstract
Non-stationarity in TS
- (previous) RevIN
- Limited to expressing basic trends
- Incapable of handling seasonal patterns.
\(\rightarrow\) Propose a new instance normalization solution
Frequency adaptive normalization (FAN)
-
Handles both dynamic trend and seasonal patterns.
-
Employs the Fourier transform
- To identify instance-wise predominant frequent components
-
Discrepancy of those frequency components between inputs and outputs
= Explicitly modeled as a prediction task
-
Model-agnostic method
1. Introduction
Toy example) Simplest non-stationary signals
- Time-variant signal with a gradually damping frequency
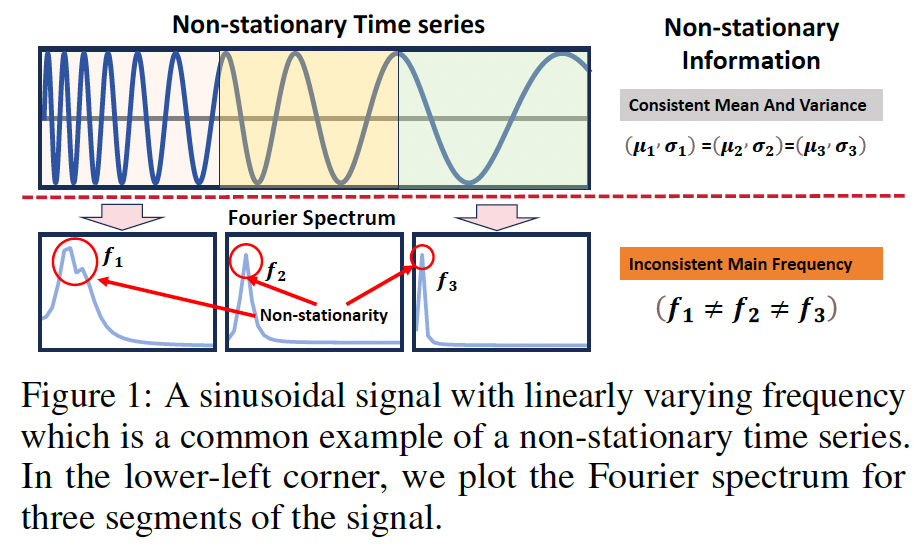
Previous methods
- Can hardly distinguish this type of change in the time domain.
\(\rightarrow\) Changes in periodic signals can be easily identified with the instance-wise Fourier transform \(\left(f_1 \neq f_2 \neq f_3\right)\).
Principal Fourier components
-
Provide a more effective representation of non-stationarity
( compared to statistical values )
Frequency Adaptive Normalization (FAN).
Mitigates the impacts from the non-stationarity, by filtering top \(K\) dominant components in the Fourier domain for each input instance,
Can handle unified non-stationary fact
- composed of both trend and seasonal patterns.
Removed patterns might evolve from inputs to outputs
\(\rightarrow\) Employ a pattern adaptation module
- To forecast future non-stationary information
Contributions
-
Limitations of RevIN in using temporal distribution statistics
\(\rightarrow\) Introduce FAN, which adeptly addresses both trend and seasonal non-stationary patterns
- Explicitly address pattern evolvement with a simple MLP
- Predicts the top \(K\) frequency signals of the horizon series
- Applies these predictions to reconstruct the output.
- Apply FAN to four general backbones
2. FAN
Problem Definition
Notation
- \(\mathcal{X} \in \mathbb{R}^{N \times D}\),
- Task: \(\mathcal{X}_{t-L: t} \rightarrow \mathcal{X}_{t+1: t+H}\),
- where \(\mathcal{X}_{t-L: t} \in \mathbb{R}^{L \times D}\) and \(\mathcal{X}_{t+1: t+H} \in \mathbb{R}^{H \times D}\).
- \(\mathbf{X}_t \in \mathbb{R}^{L \times D}\) and \(\mathbf{Y}_t \in \mathbb{R}^{H \times D}\) .
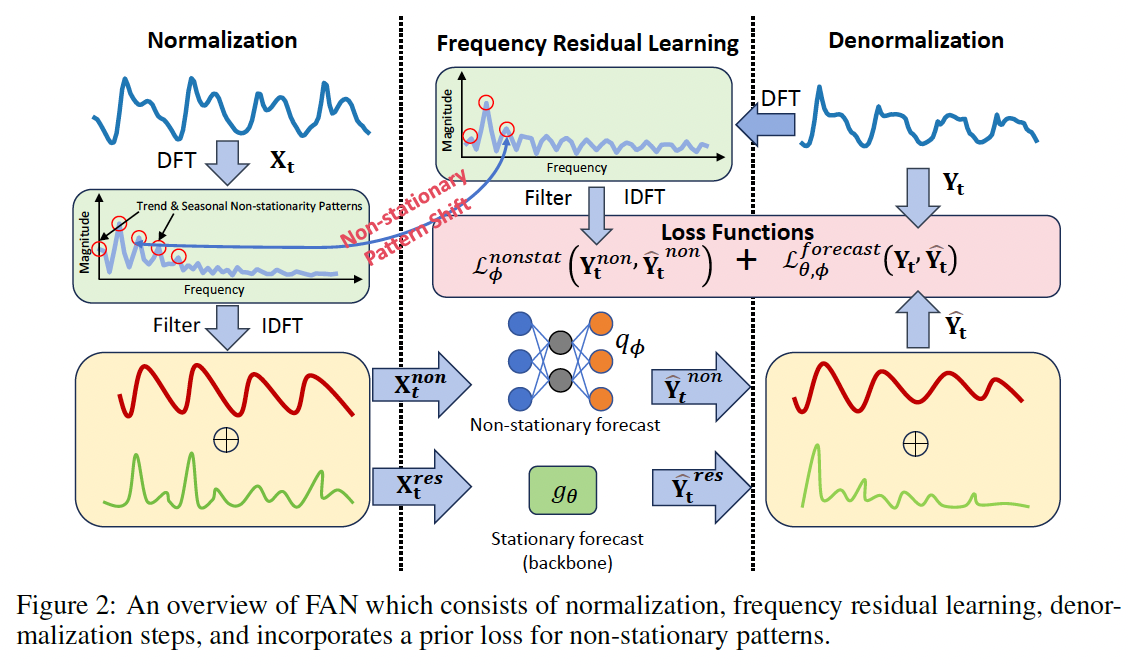
Symmetrically structured instance-wise norm & denorm
- (1) Norm: Removes the impacts of non-stationary signals
- Through frequency domain decomposition
- (2) Denorm: Addresses potential shifts in frequency components between the input and output
- Supported by a prediction module
(1) Frequency-based Normalization
Removes the top \(K\) dominant components in the frequency domain
- Backbone can concentrate on the stationary aspects
- Frequency Residual Learning (FRL)
- Apply the FRL to each dimension in a CI manner
- Restores the top \(K\) components into time domain components \(\mathbf{X}_t^{\text {non }}\) with \(\operatorname{IDFT}(\cdot)\).
- \(\mathbf{X}_t^{\text {non }}=\operatorname{IDFT}\left(\operatorname{Filter}\left(\mathcal{K}_t, \mathbf{Z}_t\right)\right)\).
- \(\mathbf{Z}_t=\operatorname{DFT}\left(\mathbf{X}_t\right)\), where \(\mathbf{Z}_t \in \mathbb{C}^{T \times D}\)
- \(\mathcal{K}_t=\operatorname{TopK}\left(\operatorname{Amp}\left(\mathbf{Z}_t\right)\right)\).
- \(\mathbf{X}_t^{\text{res}}=\mathbf{X}_t-\mathbf{X}_t^{\text{non}}\).
(2) Forecast & Denormalization
\(\hat{\mathbf{Y}}_t=\hat{\mathbf{Y}}_t^{\text {res }}+\hat{\mathbf{Y}}_t^{\text{non}}\).
- \(\hat{\mathbf{Y}}_t^{\text {res }}=g_\theta\left(\mathbf{X}_t^{\text {res }}\right)\).
- Forecast backbone model (\(g_\theta\))
\(\hat{\mathbf{Y}}_t^{\text {non }}\): with Non-stationarity shift forecasting
- Use a simple MLP model \(q_\phi\) to directly predict future values of the composite top \(K\) frequency components
-
\[\hat{\mathbf{Y}}_t^{\text {non }}=q_\phi\left(\mathbf{X}_t^{\text {non }}, \mathbf{X}_t\right)=\mathbf{W}_3 \operatorname{ReLU}\left(\mathbf{W}_2 \operatorname{Concat}\left(\operatorname{ReLU}\left(\mathbf{W}_1 \mathbf{X}_t^{n o n}\right), \mathbf{X}_t\right)\right)\]
- Since \(\mathbf{X}_t^{\text {non }}\) only contains top \(K\) frequency information, concatenate the top \(K\) components with the original input \(\mathbf{X}_t\) to handle potential frequency variations.
Loss Functions.
Incorporate a prior guidance loss
- For the prediction of principal frequency components
\(\phi, \theta=\underset{\phi, \theta}{\arg \min } \sum_t\left(\mathcal{L}_\phi^{\text {nonstat }}\left(\mathbf{Y}_t^{\text {non }}, \hat{\mathbf{Y}}_t^{\text {non }}\right)+\mathcal{L}_{\theta, \phi}^{\text {forecast }}\left(\mathbf{Y}_t, \hat{\mathbf{Y}}_t\right)\right)\).
- \(\mathcal{L}_\phi^{\text {nonstat }}\): Ensures \(q_\phi\) accurately predict the non-stationary principal frequency component
- \(\mathcal{L}_{\theta, \phi}^{\text {forecast }}\) : Guarantees that both model optimizes along the overall forecast accuracy
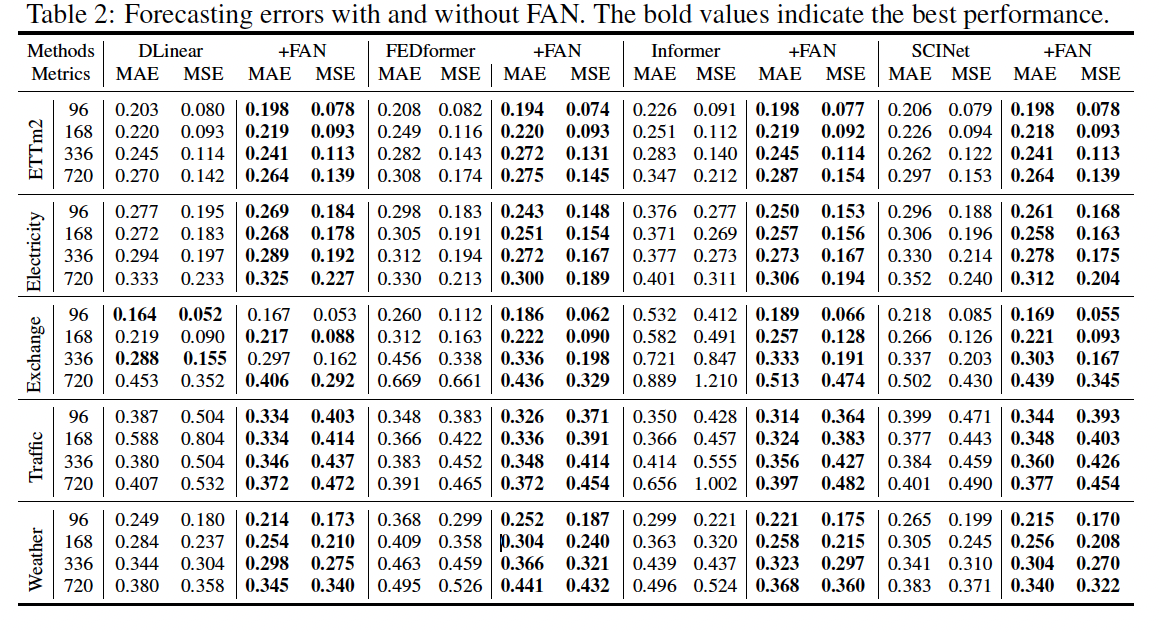
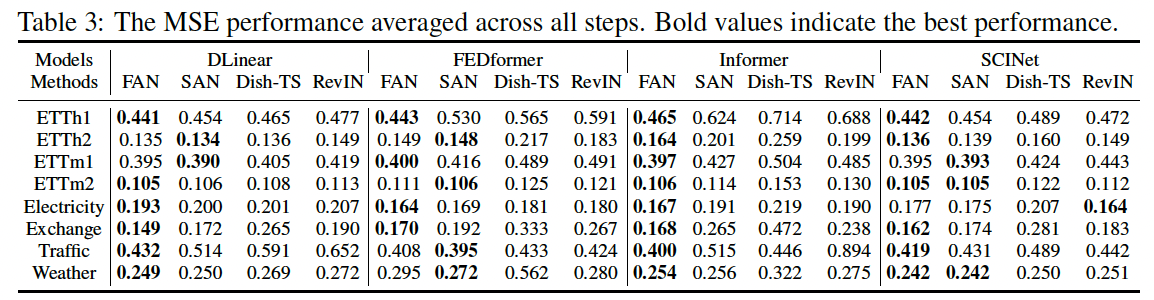
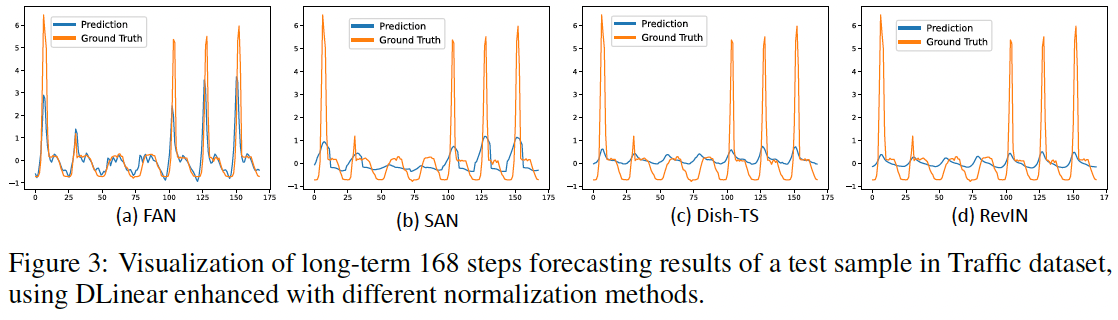
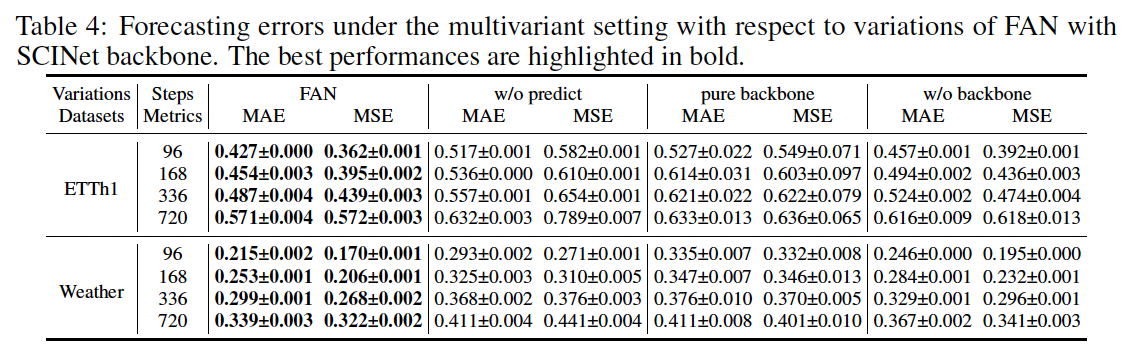
3. Experiments