GAFormer; Enhancing TS Transformers Through Group-Aware Embeddings

GAFormer: Enhancing TS Transformers Through Group-Aware Embeddings

Contents

1. Abstract
2. Preliminaries

0. Abstract

Novel approach for learning data-adaptive position embeddings

\(\rightarrow\) Incorporate learned spatial and temporal structure

How?

• Introduces “group tokens”

• Constructs an instance-specific “group embedding (GE) layer”

  • Assigns input tokens to a select number of learned group tokens

    \(\rightarrow\) Incorporating structural information into the learning process.

Group-Aware Transformer (GAFormer)

Both spatial and temporal group embeddings

\(\rightarrow\) Significantly enhance the performance of several backbones

1. Introduction

Position embeddings (PE)

• Encode the relative ordering between channels and over different points in time

Standard PE can be problematic for the following reasons

• (1) No predetermined ordering or “spatial position” for different channels in TS
• (2) Relationships across channels and time segments might be instance-specific

\(\rightarrow\) These characteristics of TS make conventional PE inadequate!

GAFormer

Learn both channel and temporal structure in TS

\(\rightarrow\) Integrate this information into our tokens through “group embeddings”

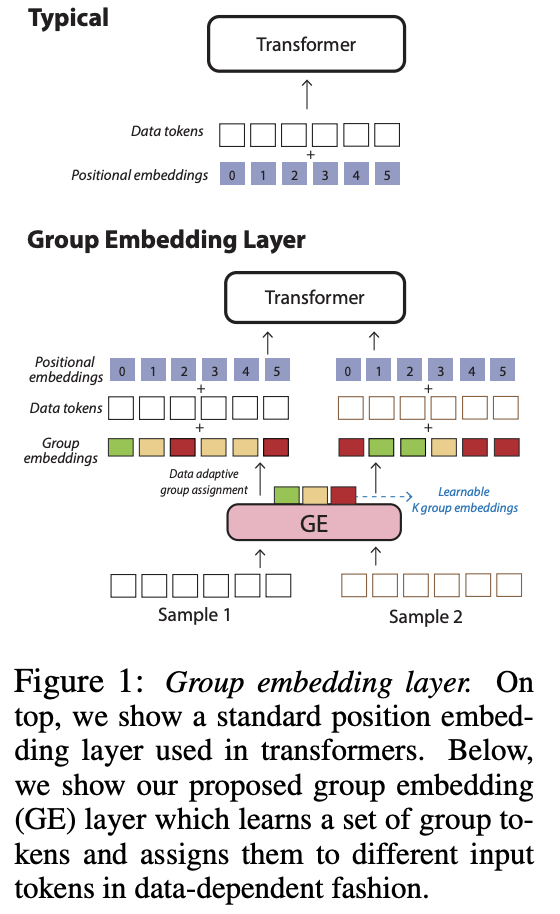
Details

• Learns a concise set of group-level tokens
• Determines how to adaptively assign them to individual samples
  • How? Based on the similarity between …
    • (1) Group embedding
    • (2) Specific sample embeddings
• Integrate both spatial and temporal group embeddings
• By decomposing grouping into either the spatial or temporal dimension, leads to enhanced interpretability

2. Method

(1) Group Embeddings

Conventional approach

• Input: Sequence of tokens \(X=\left[\mathbf{x}_1, \ldots, \mathbf{x}_N\right] \in \mathbb{R}^{N \times D}\)
• PE: \(P=\left[\mathbf{p}_1, \ldots, \mathbf{p}_N\right] \in \mathbb{R}^{N \times D}\)
• Input + PE = \(X_{P E}=\left[\mathbf{x}_1+\mathbf{p}_1, \ldots, \mathbf{x}_N+\mathbf{p}_N\right]\).

Result in \(X_{P E} \leftarrow X+P\).

Proposal

In contrast to this fixed scheme for PEs …

Group embeddings (GEs)

• In a data-adaptive manner
• Pass the input sequence to Enc \((\cdot)\)
  • Obtain \(\left[\operatorname{Enc}(X)_1, \ldots, \operatorname{Enc}(X)_N\right]\).
• Procedure
  • (1) Projection
    • Projected to \(K<D\) dimensions with \(W \in \mathbb{R}^{D \times K}\).
  • (2) Softmax
    • Effectively sparsify the coefficients that assign group tokens to input tokens
    • Select a small number of group embeddings to each token

Summary) Group embedding operation \(\mathrm{GE}(X)\)

• \(\operatorname{GE}(X)=\operatorname{SoftMax}(\operatorname{Enc}(X) \cdot W) \cdot G\).
• \(X_{G E} \leftarrow X+\operatorname{GE}(X)\).

(2) GAFormer: A Group-Aware SpationTemporal Transformer

Spatiotemporal transformer

• Concurrently extracts both temporal and spatial grouping structures, through learning group embeddings

a) Tokenization Layer

• Patchify: \(X \in \mathbb{R}^{C \times P \times L}\),
• Token Embedding: \(Z=\operatorname{Token}(X) \in \mathbb{R}^{C \times P \times D}\).
  • via Transformer + learnable PE, in a CI manner

b) Spatial Group Embeddings

For Channel-wise interactions

• Slice TS spatially
  • Result: \(Z_S\) = Set of \(P\) sequences of length \(C\).
• Use group embedding strategy to learn spatial structure
  • with spatial group embedding (SGE) layer
• Result: Spatial set of group tokens \(G_S \in \mathbb{R}^{K_S \times D}\),
  • where \(K_S\) is the number of groups
• Spatial operations: \(Z^{\prime}=\operatorname{Trans-S}\left(Z_S+\operatorname{SGE}\left(Z_S\right)\right)\).
  • Trans-S \((\cdot)\): Spatial transformer encoder
    • Operates on sequences of tokens that are at the same point in time but vary across their channel
    • Effect: Extract different spatial groupings for each time period.

c) Temporal Group Embeddings

For Temporal interactions

• Use dimension reduction layer \(H(\cdot)\)

  • Result: \(Z_T=\) \(H\left(\left[Z_1^{\prime}, \ldots, Z_P^{\prime}\right]\right) \in \mathbb{R}^{P \times D^{\prime}}\),
    • where \(C\) channels of \(D\)-dim tokens are bottlenecked into one token of \(D^{\prime}\)-dim

• Use group embedding strategy to learn temporal structure

  • with temporal group embedding (TGE) layer

• Temporal operation: \(Z^{\text {final }}=\text { Trans- } \mathrm{T}\left(Z_T+\operatorname{TGE}\left(Z_T\right)\right)\)

  • Trans-T : Temporal transformer encoder

GAFormer maintains a temporal set of group tokens:

• \(G_T \in \mathbb{R}^{K_T \times D^{\prime}}\) with \(K_T\) groups.