InjectTST; A Transformer Method of Injecting Global Information into Independent Channels for Long Time Series Forecasting

InjectTST: A Transformer Method of Injecting Global Information into Independent Channels for Long Time Series Forecasting

Contents

1. Abstract
2. Introduction
   1. CI vs. CM
   2. InjectTST
   3. Contributions
3. Methodology
   1. CI Backbone
   2. Global Mixing Module
   3. Self-Contextul Attention Module

0. Abstract

CI > CD??

Channel dependency remains an inherent characteristic of MTS,

Designing a model that incorporates merits of both

• (1) channel-independent
• (2) channel-mixing

InjectTST

Instead of designing a CM model,

Retain the CI backbone

& gradually inject global information into individual channels in a selective way

Modules

• (1) Channel identifier
  • Help Transformer distinguish channels for better representation.
• (2) Global mixing module
  • Produces cross-channel global information
• (3) Self-contextual attention module
  • Independent channels can selectively concentrate on useful global information without robustness degradation, and channel mixing is achieved implicitly.

1. Introduction

(1) CI vs. CM

Advantages of CI

• (1) Noise mitigation:

  • Focus on individual channel forecasting,

    without being disturbed by noise from other channels

• (2) Distribution drift mitigation:

  • Alleviate the distribution drift problem of MTS

Advantages of CM

• (1) High information capacity:
  • Excel in capturing channel dependencies
  • Bring more information to the forecasting
• (2) Channel specificity:
  • Carried out simultaneously, enabling the model to fully capture the distinct characteristics of each channel

Goal: design an effective model with merits of both CI & CD

Challenges of CI + CM

• (CI) Inherently contradictory to channel dependencies
• (CM) Existing denoising methods and distribution drift-solving methods still struggle to make CM frameworks as robust as CI

(2) InjectTST

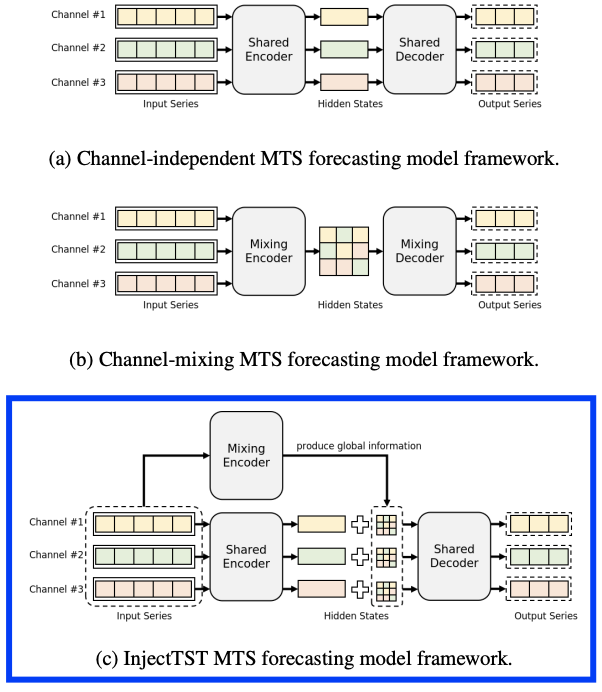
Components

• (1) Channel identifier
• (2) Global mixing module
• (3) Self-contextual attention (SCA)

a) Channel identifier

• Trainable embedding for each channel
  • extracting unique representation of channels
• Distinguishing channels for the Transformer in the injection period

b) Global mixing module

• Produce global information for subsequent injection
• Transformer encoder is used for a high-level global representation.

c) Self-contextual attention (SCA)

• For harmless information injection
• Context = Global information
  • Injection via a modified cross attention , with minimal noise disturb.

(3) Contributions

1. Both CI & CM

   • CI as backbones

   • CM information is viewed as context

     & injected into individual channels in a selective way

2. Inject TST
   • Injection MTS forecasting method for global information into CI Transformer models
   • (1) Channel identifier: to identify each channel
   • (2) Two kinds of global mixing modules: mix channel information effectively
   • (3) Cross attention-based SCA module: to inject valuable global information into individual channels.
3. Experiments

2. Methodology

Notation

• Input MTS \(\boldsymbol{X}=\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_L\right)\),
  • \(\boldsymbol{x}_t=\) \(\left(x_{t, 1}, x_{t, 2}, \ldots, x_{t, M}\right), t=1,2, \ldots, L\).
• Target MTS \(\boldsymbol{Y}=\left(\boldsymbol{x}_{L+1}, \ldots, \boldsymbol{x}_{L+T}\right)\).

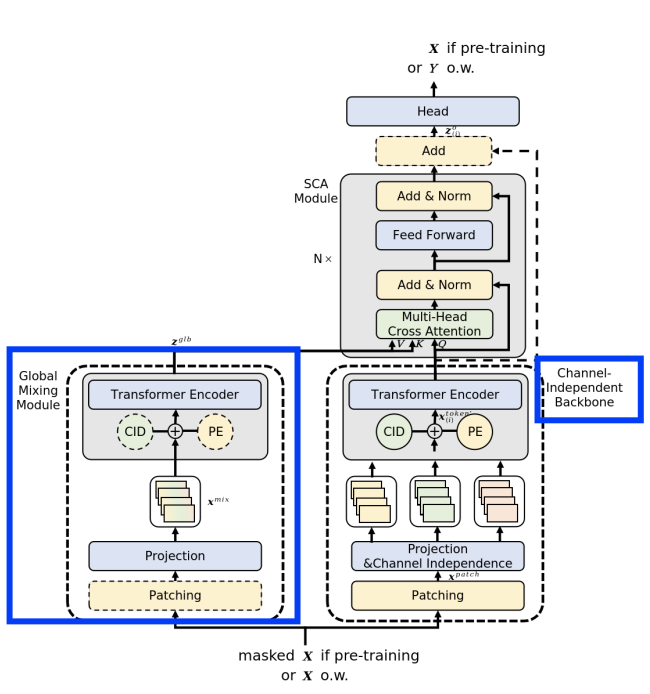
(1) CI Backbone

a) Patching and Projection

\(\boldsymbol{x}^{\text {token }}=\boldsymbol{x}^{\text {patch }} \boldsymbol{W}+\boldsymbol{U}\).

• where the output \(\boldsymbol{x}^{\text {token }} \in \mathbb{R}^{M \times P N \times D}\).

[Patching]

• Before) \(\boldsymbol{X} \in \mathbb{R}^{L \times M}\)
• After) \(\boldsymbol{x}^{\text {patch }} \in \mathbb{R}^{M \times P N \times P L}\),
  • \(P L\) : the length of each patch
  • \(P N\) : the number of patches in each channel

[Linear projection]

• Projection: \(\boldsymbol{W} \in \mathbb{R}^{P L \times D}\) ,
• Learnable positional encoding: \(\boldsymbol{U} \in \mathbb{R}^{P N \times D}\)

b) Channel Identifier

CI = treats channels with a shared model \(\rightarrow\) Cannot distinguish the channels ( = lacking channel specificity )

Channel identifier

\(\boldsymbol{x}^{\text {token' }}=\boldsymbol{x}^{\text {token }}+\boldsymbol{V}=\boldsymbol{x}^{\text {patch }} \boldsymbol{W}+\boldsymbol{U}+\boldsymbol{V} \text {. }\).

• Learnable tensor \(\boldsymbol{V} \in \mathbb{R}^{M \times D}\).

\(\boldsymbol{z}_{(i)}=\text { Encoder }^{\text {ci }}\left(\boldsymbol{x}_{(i)}^{\text {token' }}\right), i=1,2, \ldots, M\).

• \(\boldsymbol{x}^{\text {token' }}\) is input into the “CI” Transformer encoder

(2) Global Mixing Module

Input: \(\boldsymbol{X}\)

Goal: Produce global information & Inject into eaach channel

Two kinds of effective global mixing modules

• (a) CaT (channel as a token)
• (b) PaT (patch as a token)

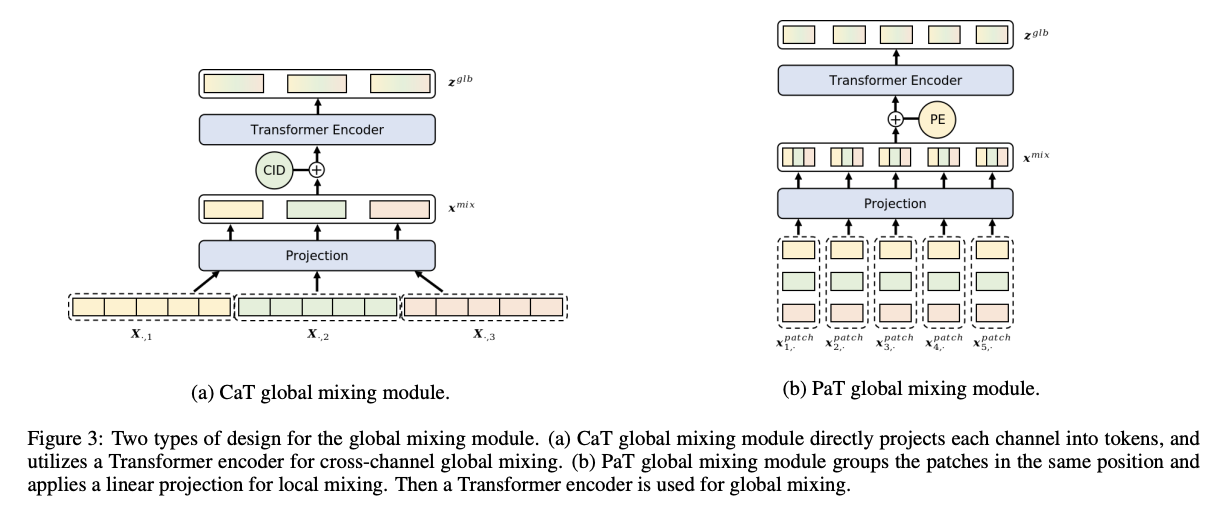
a) CaT Global Mixing Module

Directly projects each channel into a token.

\(\boldsymbol{x}^{m i x}=\boldsymbol{X}^{\mathrm{T}} \boldsymbol{W}_{\text {mix }}\).

• \(\boldsymbol{W}_{\text {mix }} \in \mathbb{R}^{L \times D}\).
• \(\boldsymbol{x}^{m i x} \in \mathbb{R}^{M \times D}\).

Final global information

\(\boldsymbol{z}^{g l b}=\text { Encoder }{ }^{\text {mix }}\left(\boldsymbol{x}^{\text {mix }}+\boldsymbol{V}\right)\).

• channel identifier \(\boldsymbol{V}\)

b) PaT Global Mixing Module

Fuses information within the patch level

\(\boldsymbol{x}^{\text {mix }}=\boldsymbol{x}^{\text {patch }} \boldsymbol{W}_{\text {mix }}\).

• Reshapes the patches into dimensions of \(P N \times(M \cdot P L)\)
• \(\boldsymbol{W}_{\text {mix }} \in \mathbb{R}^{(M \cdot P L) \times D}\) is applied on the grouped patches.
• \(\boldsymbol{x}^{m i x} \in \mathbb{R}^{P N \times D}\).

Final global information

\(\boldsymbol{z}^{g l b}=\text { Encoder }^{\text {mix }}\left(\boldsymbol{x}^{\text {mix }}+\boldsymbol{U}\right)\).

• positional encoding \(\boldsymbol{U}\)

\(\rightarrow\) PaT is more stable, while CaT is outstanding in some special datasets

(3) Self-Contextual Attention Module

Must inject global information into each channel ***with minimal impact on the robustnessv

\(\rightarrow\) use cross attention

\(\boldsymbol{z}_{(i)}^o=\operatorname{SCA}\left(\boldsymbol{z}_{(i)}, \boldsymbol{z}^{g l b}, \boldsymbol{z}^{g l b}\right)\).

• [K,V] context \(\boldsymbol{z}^{g l b}\)
• [Q] channel information \(\boldsymbol{z}_{(i)}\)

Others

• Finally, a linear head is appended to produce the prediction

• SSL as PatchTST