TOTEM; TOkenized Time Series EMbeddings for General Time Series Analysis

TOTEM: TOkenized Time Series EMbeddings for General Time Series Analysis

Contents

1. Abstract

0. Abstract

Unified modeling

• (1) common backbone
• (2) unification across tasks and domains

Discrete, learnt, TS data representations

\(\rightarrow\) Enable generalist, cross-domain training

TOTEM

TOkenized Time Series EMbeddings

• Simple tokenizer architecture

  • embeds TS data from varying domains

    using a discrete vectorized representation

• Learned via SSL

• Works across multiple tasks and domains

• Minimal to no tuning

Experiments

• Extensive evaluation on 17 real world TS datasets across 3 tasks
• Specialist (i.e., training a model on each domain)
• Generalist (i.e., training a single model on many domains)

https://github.com/SaberaTalukder/TOTEM.

1. Introduction

(1) Specialist vs. Generalist

( = in terms of dataset, not task )

Specialist-training ( = Previous works )

• trained on a single TS domain

Generalist-training

• simultaneously trained on multiple TS domains

\(\rightarrow\) Both can be tested under various regimes

• (1) In-domain testing
• (2) Zero-shot testing ( = cross-domain setting )

(2) Zero-shot forecasting

case 1) Forecaster ~

• trains on one dataset
• then predicts on a separate dataset

case 2) Forecaster ~

• trains on a subset of channels (which we call sensors) from one dataset
• then zero-shot forecasts on the remaining sensors in the same dataset

\(\rightarrow\) Both are specialists!

( \(\because\) trained on only one (or a subset of one) dataset )

(3) Restricted by task!

Methods study only single test!

• forecasting (Wu et al., 2021; Woo et al., 2022)
• anomaly detection (Xu et al., 2021; He & Zhao, 2019)
• …

Recently, Unified w.r.t model architecture

• ex) exploring language and vision backbones on various TS tasks

  (Zhou et al., 2023; Wu et al., 2022a)

\(\rightarrow\) Still… utilize specialist training :(

(4) Quantization / Discrete

Vector quantized variational autoencoders (VQVAEs)

Goal of this paper

• Develop a streamlined framework for learning a tokenized data representation (using VQVAEs)
• broad range of tasks & data domains
• minimal to no tuning

Explore the value of a VQVAE-based tokenizer for …

• Imputation
• Anomaly detection
• Forecasting

Utilize SSL + Discrete tokens

(5) Contributions

1. Propose TOTEM

   • Simple tokenizer architecture for TS analysis
   • Works across domains and tasks
   • Minimal to no tuning.

2. SOTA results

3. Extensive evaluation in the generalist setting

   ( = training a single model on multiple domains)

   ( + in in-domain and zero-shot testing regimes )

3. Method

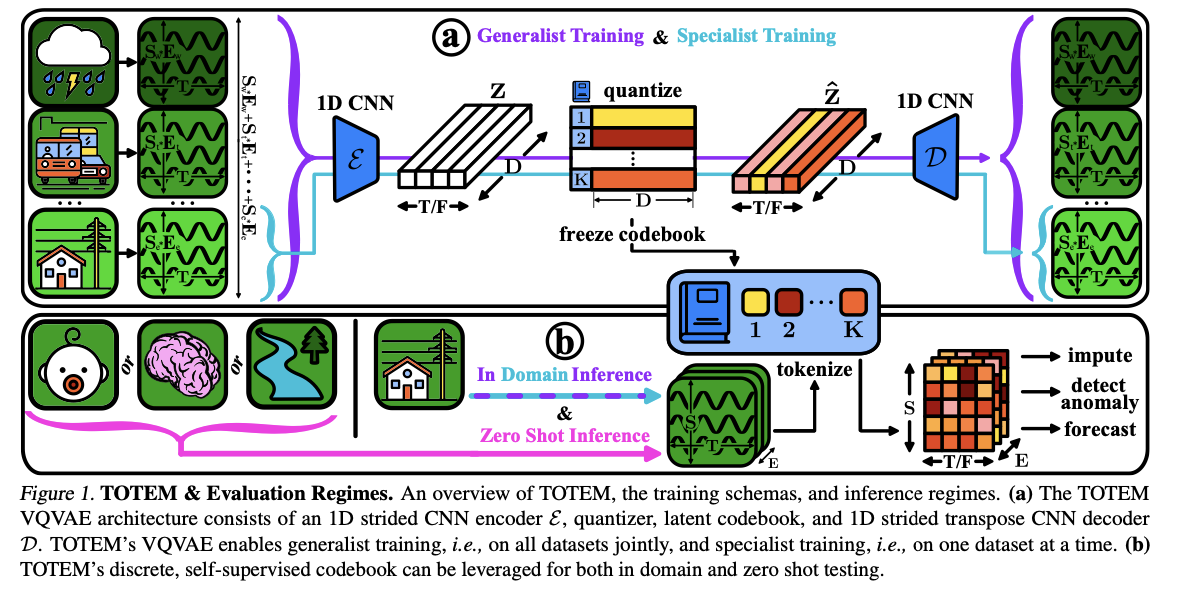
(1) Outline

DISCRETE TS tokenization

(1) Enables the design of GENERAL models

• across a variety of TS domains, tasks

(2) Design a SINGLE tokenizer architecture

• generally applicable without extensive data engineering
• suitable for varying data dimensionalities across different tasks.

(2) Data Engineering

Operate directly on time steps! ( less DE )

\(\rightarrow\) Enables generalist-training!

• as differing data domains have widely varying sampling rates leading to distinct auxiliary features and frequency profiles.

(3) Varying Dimensionality

Notation

• \(E\) examples (i.e. number of distinct recordings)
• \(S\) sensor channels
• \(T\) time steps

\(\rightarrow\) Formally expressed as \(\left\{\mathbf{x}_j\right\}_{j=1}^E \subset \mathbb{R}^{S \times T}\).

Even within a single task and single data domain

( = where \(S\) does not change )

\(\rightarrow\) \(E\) and \(T\) take on a wide range of values.

Tokenizer of TOTEM

• handles varying dimensionality across \(E, S\), and \(T\)
• by creating non-overlapping tokens along the time-dimension

(4) Differing Tasks

Three tasks

• (1) Imputation
  • 1-1) intake a masked TS \(\mathbf{x}_{\mathrm{m}} \in \mathbb{R}^{S \times T_{\text {in }}}\)
  • 1-2) reconstruct and impute \(\mathrm{x} \in \mathbb{R}^{S \times T_{\mathrm{in}}}\)
• (2) Anomaly detection
  • 2-1) intake a corrupted TS \(\mathbf{x}_{\text {corr }} \in \mathbb{R}^{S \times T_{\text {in }}}\)
  • 2-2) reconstruct \(\mathbf{x} \in \mathbb{R}^{S \times T_{\text {in }}}\).
• (3) Forecasting
  • 3-1) intake \(\mathbf{x} \in \mathbb{R}^{S \times T_{\text {in }}}\)
  • 3-2) predicts \(\mathbf{y} \in \mathbb{R}^{S \times T_{\text {out }}}\)

TOTEM’s tokenizer is performant across all tasks

(5) TOTEM Implementation

Single tokenizer architecture

• Enables generalist modeling
  • across differing domains and tasks
• Inspiration from the VQVAE

Original VQVAE: Dilated CNN

• ( stride=2, window-size=4 )
• operate on a larger input area / coarser scale
• rooted in the high sampling rates of raw audio waveforms
  • sampling rates are not a trait shared by many TS domains.

When adapting the VQVAE for general TS analysis….

TOTEM VQVAE

1. Operates directly on time steps ( = no data engineering )

2. Creates discrete, non-overlapping tokens

   • along the time dimension of length \(F\), where \(F<T\),

   • Enables training and testing on variable length

3. Maintains the same architecture and objective

   ( regardless of the downstream task )

4. Aims to capture maximal information within a large receptive field by:

   • (1) using a strided non-causal CNN w/o dilation

   • (2) training on long TS inputs

   • (3) pre-striding the data by a stride of 1

     ( so the tokenizer learns from maximal inputs )

Architecture

1. Encoder \(\mathcal{E}\)

   • strided 1D convolutions compressing the TS by a cumulative stride of \(F\).

2. Quantizer

3. Latent codebook \(\mathcal{C}=\left\{\mathbf{c}_i\right\}_{i=1}^K\)

   • consists of \(K D\)-dim codewords \(\mathbf{c}_i \in \mathbb{R}^D\).

4. Decoder \(\mathcal{D}\)

   • reverse architecture of the encoder \(\mathcal{E}\),

   • consisting of \(1 \mathrm{D}\) transpose convolutions

     ( with a cumulative stride of \(1 / F\) )

Procedure

Step 1) Takes in UTS \(\left\{\mathbf{x}_i \in \mathbb{R}^T\right\}_{i=1}^{E \cdot S}\)

• obtained by flattening the sensor channel of MTS

• makes TOTEM’s VQVAE sensor-agnostic

  \(\rightarrow\) Enabling TOTEM’s generalist-training and zero-shot-testing

Step 2) Encoder \(\mathcal{E}\) maps …

• UTS \(\mathbf{x} \in \mathbb{R}^T\)
• to \(\mathbf{z}=\mathcal{E}(\mathbf{x}) \in \mathbb{R}^{T / F \times D}\),

Step 3) Via codebook…

• Replace \(\mathbf{z}\) with \(\hat{\mathbf{z}} \in \mathbb{R}^{T / F \times D}\)
  • such that \(\hat{\mathbf{z}}_j=\mathbf{c}_k\), where \(k=\arg \min _i \mid \mid \mathbf{z}_j-c_i \mid \mid _2\).

Step 4) Decoder \(\mathcal{D}\)

• Map the quantized \(\hat{\mathbf{z}}\) to a reconstructed TS \(\hat{\mathbf{x}}=\mathcal{D}(\hat{\mathbf{z}}) \in \mathbb{R}^T\).

Summary

• Learn \(\mathcal{E}, \mathcal{D}\), and \(\mathcal{C}\) by optimizing the \(\mathcal{L}=\mathcal{L}_{\text {rec }}+\alpha \cdot \mathcal{L}_{\mathrm{cmt}}\)
  • Reconstruction loss \(\mathcal{L}_{\text {rec }}=\frac{1}{E \cdot S} \sum_i \mid \mid \mathbf{x}_i-\hat{\mathbf{x}}_i \mid \mid _2^2\)
  • Commitment loss \(\mathcal{L}_{\mathrm{cmt}}\),
    • which allows the codebook to update despite the the nondifferentiable arg min operation during quantization.

Imputation & Anomaly detection

• can be directly solved with just TOTEM’s VQVAE

  (\(\because\) they are fundamentally data representation tasks )

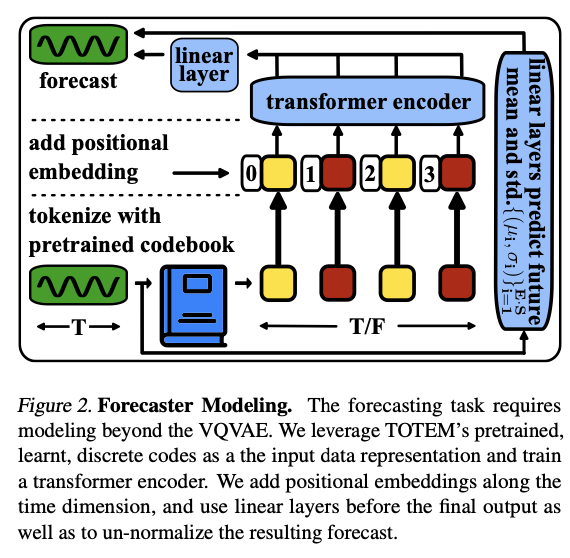
Forecasting

( = further modeling is required ( Figure 2 ) )

• Step 1) Via trained code book …

  convert \(\mathbf{x}_s \in \mathbb{R}^{T_{\text {in }}}\) to a sequence of \(T_{\text {in }} / F\) discrete tokens.

• Step 2-1) Via Forecaster (1) transformer encoder …

  ( = multi-head attention layers )

  • processes these tokenized TS independently for each sensor
  • adding time-based positional encodings
  • predicts the forecasted measurements \(\overline{\mathbf{y}}_s \in \mathbb{R}^{T_{\text {out }}}\) for \(s=1, \ldots, S\),

• Step 2-2) via Forecaster (2)

  • takes in \(\mathbf{x}_s\) and predicts \(\mu_s\) and \(\sigma_s\), for each sensor \(s=1, \ldots, S\) to unnormalize the data.

• Step 3) Result: \(\mathbf{y}_s=\sigma_s \cdot \overline{\mathbf{y}}_s+\mu_s\).

The forecaster is trained in a supervised fashion

4. Experimental Setup

(1) Overview

Specialist

• training on a single domain (Tables 1, 3, 5)

Generalist

• training on multiple domains (Tables 2, 4, 6)

In-domain

• testing on the training domain

Zero-shot

• testing on a separate domain from training.

(2) Setup

• Three random seeds
• Evaluation metrics
  • MSE (↓), MAE (↓), precision P (↑), recall R (↑), and F1 score (↑)
  • As various metrics .. \(\rightarrow\) Average number of best results

(3) Baselines

Two families of approaches

• (multitask) for multiple tasks
  • GPT2, TimesNet
• (singletask) for a specific task
  • others

(4) 17 Datasets

12 benchmark datasets

• weather [W], electricity [E], traffic [T], ETTm1 [m1], ETTm2 [m2], ETTh1 [h1], ETTh2 [h2], SMD, MSL, SMAP, SWAT, PSM
• commonly used for
  • imputation
  • anomaly detection
  • forecasting

( + for Zero shot settings )

5 benchmark datasets

• neuro2 [N2], neuro5 [N5], and saugeen river flow [R], U.S. births [B], and sunspot [S]

5. Imputation

Input & Output

• Input: masked time series \(\mathbf{x}_{\mathrm{m}} \in\) \(\mathbb{R}^{S \times T_{\text {in }}}\)
• Output: \(\mathbf{x} \in \mathbb{R}^{S \times T_{\text {in }}}\)

Four canonical masking percentages

• \[12.5 \%, 25 \%, 37.5 \%, 50 \%\]

Metric: MSE and MAE

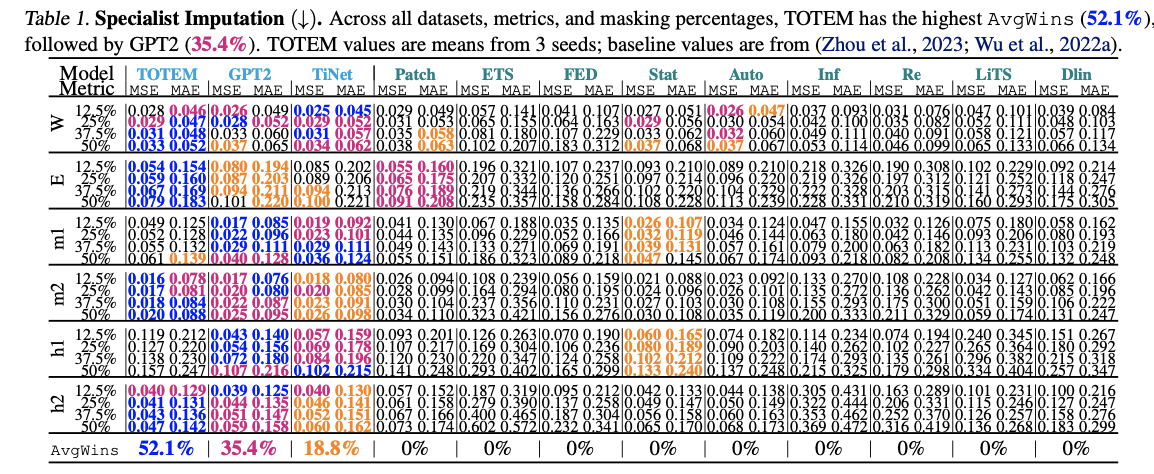
(1) Specialict

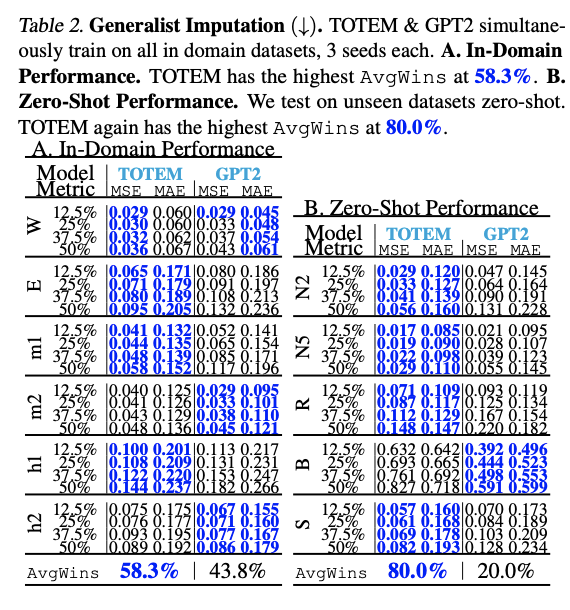
(2) Generalist

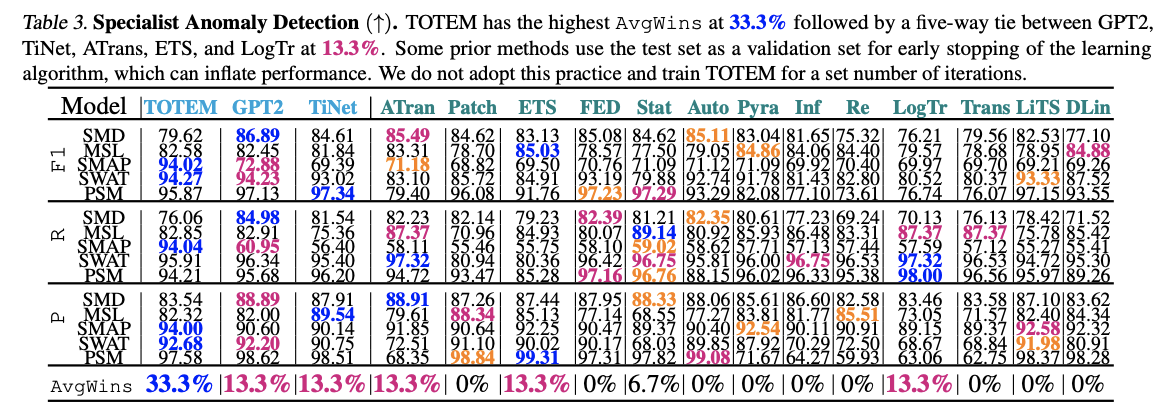
6. Anomaly Detection

Input & Output

• Input: corrupted time series \(\mathbf{x}_{\text {corr }} \in \mathbb{R}^{S \times T_{\text {in }}}\)
• Output: \(\mathbf{x} \in \mathbb{R}^{S \times T_{\text {in }}}\)

Amount of corruption is considered known, at \(\mathrm{A} \%\).

Metric: Precision P ( \(\uparrow\) ), Recall R ( \(\uparrow\) ), and F1 Score ( \(\uparrow\) ).

Etc

• Several prior works: use the test set as a validation set for early stopping!!!!
• TOTEM: have a held out test set

(1) Specialist

(2) Generalist

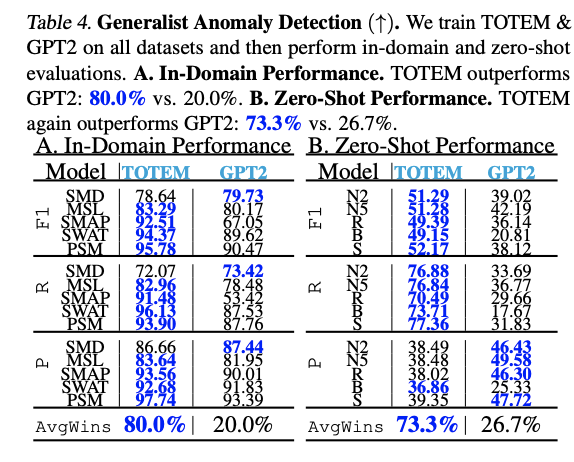
~ ing …