TiVaT; Jonit-Axis Attention for TIme Series Forecasting with Lead-Lag Dynamics

TiVaT: Jonit-Axis Attention for TIme Series Forecasting with Lead-Lag Dynamics

Contents

1. Abstract
2. Introduction
3. Methodology

0. Abstract

Simultaneously capturing both TD & CD (VD) remains a challenging

Previous works

• CD models: handle these dependencies separately
• Limitation in lead-lag dynamics.

TiVaT (Time-Variable Transformer)

(1) Integrates TD& VD via Joint-Axis (JA) attention

• Capture variate-temporal dependencies

(2) Further enhanced by Distance-aware Time-Variable (DTV) Sampling

• Reduces noise and improves accuracy through a learned 2D map that focuses on key interactions

1. Introduction

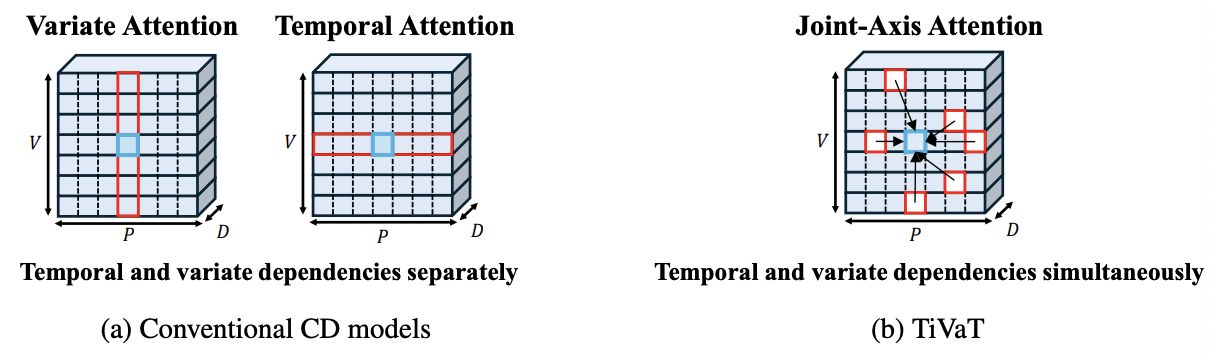
CD models = Handle temporal and inter-variable dependencies separately

\(\rightarrow\) Limiting their ability to capture more complex interactions between variables and temporal dynamics

( i.e. lead-lag relationships )

Why not do both?

\(\rightarrow\) Significant increase in computational cost and model complexity

TiVaT (Time-Variable Transformer)

Capture both temporal and variate dependencies simultaneously

Joint-Axis (JA) attention mechanism

A key feature of TiVaT

= Integration of offsets inspired by

• deformable attention (Zhu et al., 2020)
• Distance-aware Time-Variable (DTV) Sampling

DTV Sampling technique

Constructs a learned 2D map to capture both spatial and temporal distances between variables and time steps

• Not only reduces computational overhead
• But also mitigates noise!

\(\rightarrow\) Scale efficiently to high-dimensional datasets without sacrificing performance.

Incorporates TS decomposition

• To capture long-term trends and cyclical patterns

2. Methodology

Notation

• \(\mathbf{X}=\left\{\mathbf{x}_{T-L_H+1}, \ldots, \mathbf{x}_T\right\} \in \mathbb{R}^{L_H \times V}\) .
  • \(\mathbf{X}_{(t,:)} \in \mathbb{R}^V\),
  • \(\mathbf{X}_{(:, v)} \in \mathbb{R}^{L_H}\),
• \(\mathbf{Y}=\left\{\mathbf{x}_{T+1}, \ldots, \mathbf{x}_{T+L_F}\right\} \in \mathbb{R}^{L_F \times V}\).

MTS forecasting is challenging because it requires capturing complex relationships along both the variate and temporal axes

(1) Overview

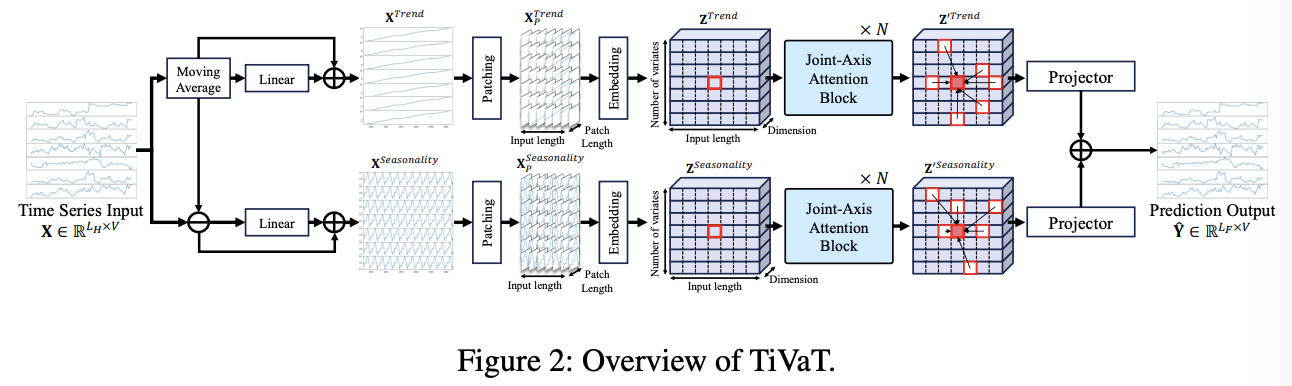
\(\begin{aligned} \mathbf{X}^{\text {Trend }} & =M A(\mathbf{X}) \\ \mathbf{X}^{\text {Seasonality }} & =\mathbf{X}-\mathbf{X}^{\text {Trend }} \\ \mathbf{X}^{\text {Trend }} & =\mathbf{X}^{\text {Trend }}+\text { Linear }\left(\mathbf{X}^{\text {Trend }}\right) \\ \mathbf{X}^{\text {Seasonality }} & =\mathbf{X}^{\text {Seasonality }}+\text { Linear }\left(\mathbf{X}^{\text {Seasonality }}\right), \end{aligned}\).

Decomposed components

• \(\mathbf{X}^{\text {Trend }}\) and \(\mathbf{X}^{\text {Seasonality }}\)
• Processed through separate sibling architectures

Architectures

• (1) Patching + Embedding
  • 1-1) Patch: \(X_P \in \mathbb{R}^{L_N} \times V \times L_P\)
  • 1-2) Token: \(Z \in \mathbb{R}^{L_N \times V \times D}\)
    • Via embedding layer \(E: \mathbb{R}^{L_N \times V \times L_P} \rightarrow \mathbb{R}^{L_N \times V \times D}\)
• (2) JA attention blocks
• (3) Projector
  • 3-1) Trend prediction
  • 3-2) Seasonality prediction
  • Common predictor
    • \(\operatorname{Proj}: \mathbb{R}^{L_N \times V \times D} \rightarrow\) \(\mathbb{R}^{L_F \times V}\)

Summary

• \(\hat{\mathbf{Y}}=\operatorname{Proj}\left(\operatorname{Enc}\left(E\left(X_P^{\text {Trend }}\right)+P E\right)\right)+\operatorname{Proj}\left(\operatorname{Enc}\left(E\left(X_P^{\text {Seasonality }}\right)+P E\right)\right)\).

(2) Joint-Axis Attention Module

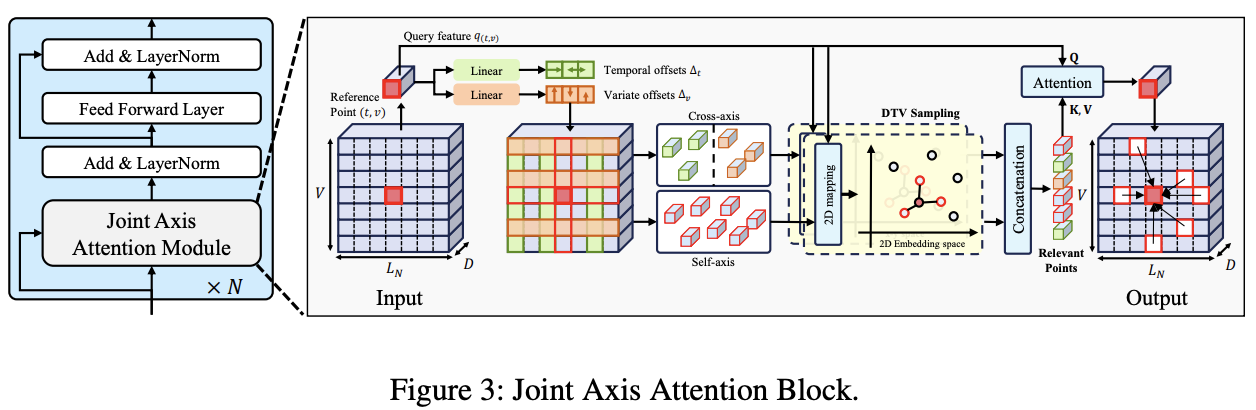
Joint-Axis Attention block

• Transformer encoder block
  • Replacing self-attention with the JA attention module

• Inspired by Deformable attention module (Zhu et al., 2020),

  = Capture relationships between a feature vector \(Z_{(t, v)}\) and other feature vectors \(Z_{\left(t^{\prime}, v^{\prime}\right)}\), where \(t \neq t^{\prime}, v \neq v^{\prime}\), or both.

• Unlike the deformable attention, the JA attention module uses offset points as guidelines to minimize information loss

• Uses the DTV sampling to capture relationships with other points that are highly relevant

• Efficient compared to full attention
  • As it avoids processing less relevant points

Deformable Attention

Introduced to tackle the inefficiencies of self-attention operations in CV

How does it work?

• Extracts offset points

  • based on the query feature \(q_{(t, v)}\) at the reference point \((t, v)\)

• Attention operation is performed accordingly

• Efficiently consider all axes,

  while also offering computational efficiency compared to self-attention at every location.

[ Fig. 3 ]

• \(Z \in \mathbb{R}^{L_N \times V \times D}\).

  • [TS] Temporal & variable axes
  • [CV] Width & height axes

• Offset points can indentify relationships between

  • the reference point
  • the other data points

  across both axes.