VCformer; Variable Correlation Transformer with Inherent Lagged Correlation for MTS Forecasting

VCformer: Variable Correlation Transformer with Inherent Lagged Correlation for Multivariate Time Series Forecasting

Contents

1. Abstract
2. Introduction
3. Related Works
4. Method
   1. Background
   2. Structure Overview
   3. Variable Correlation Attention

0. Abstract

Vanilla point-wise self-attention mechanism ?? NO!

Variable Correlation Transformer (VCformer)

• Utilizes Variable Correlation Attention (VCA) module
  • to mine the correlations among variables
• VCA calculates and integrates the cross-correlation scores corresponding to different lags between queries and keys
• Koopman Temporal Detector (KTD)
  • to better address the non-stationarity in TS

\(\rightarrow\) Extract both multivariate correlations and temporal dependencies

https://github.com/CSyyn/VCformer.

1. Introduction

Addressing the limitations of vanilla variable point-wise attention

Variable Correlation Transformer (VCformer)

• Exploit lagged correlation inherent in MTS

  • through the Variable Correlation Attention (VCA) module

• VCA module

  • calculates the global strength of correlations between each query and key across different feature.

  • Not only computes autocorrelations akin to those in Autoformer

    But also extends this concept to determine lagged crosscorrelations among various variates.

• ROLL operation + Hadamard products
  • to approximate these lagged correlations effectively
• Adaptively aggregates lagged correlation over various lag lengths
• Koopman Temporal Detector (KTD) module
  • inspired by Koopman theory in dynamics

Contributions

1. VCformer
   • Both variable correlations and temporal dependencies of MTS.
2. Two things
   1. Fully exploit lagged correlations among different variates
   2. KD to effectively address non-stationarity
3. SOTA

2. Related Works

CI vs. CD

pass

iTransformer [Liu et al., 2023a]

• revolutionizes the vanilla Transformer
• By inverting the duties of the
• (1) traditional attention mechanism
• (2) feed-forward network
• Roles
  • (1) Capturing multivariate correlations
  • (2) Learning nonlinear representations
• Adopt the classical self-attention mechanism based on point-wise method, which does not fully exploit the relationship among variable sequences.

3. Method

Input: \(\mathbf{X}=\) \(\left\{\mathbf{x}_1, \ldots, \mathbf{x}_T\right\} \in \mathbb{R}^{T \times N}\)

Target: \(\mathbf{Y}=\left\{\mathbf{x}_{T+1}, \ldots, \mathbf{x}_{T+H}\right\} \in\) \(\mathbb{R}^{H \times N}\)

(1) Background

1. Limitation of vanilla variable attention
   • in modelling feature-wise dependencies.
2. Variable cross-correlation attention mechanism
   • operates across the feature channels
3. Koopman theory
   • Treat TS as dynamics
4. KTD module
   • Combine it with the variable cross-correlation attention
   • To learn both channels and time-steps dependencies

a) Limitation of Vanilla Variable Attnetion

Self-attention module

• employs the linear projections to get \(\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{T \times D}\),
  • \(Q=\left[\mathbf{q}_1, \mathbf{q}_2, \ldots, \mathbf{q}_T\right]^{\top}\) ,
  • \(K=\left[\mathbf{k}_1, \mathbf{k}_2, \ldots, \mathbf{k}_T\right]^{\top}\),
• Pre-Softmax attention score
  • \(\mathbf{A}_{i, j}=\) \(\left(\mathbf{Q K}^{\top} / \sqrt{D}\right)_{i, j} \propto \mathbf{q}_i^{\top} \mathbf{k}_j\).

Nevertheless, feature-wise information,

( where each of the \(D\) features corresponds to an entry of \(\mathbf{q}_i \in \mathbb{R}^{1 \times D}\) or \(\mathbf{k}_j \in \mathbb{R}^{1 \times D}\) )

\(\rightarrow\) Absorbed into such inner-product representation :(

iTransformer [Liu et al., 2023a]

• inverted Transformer, to capture cross-variable dependencies

  • instead computes \(K^{\top} Q \in \mathbb{R}^{D \times D}\).

• Suitable for capturing instantaneous cross-correlation,

  but it is insufficient for MTS data which is coupled with the intrinsic temporal dependencies.

\(\rightarrow\) Variates of MTS data can be correlated with each other, yet with a lag interval!!

( = lagged cross-correlation in MTS analysis [John and Ferbinteanu, 2021; Chandereng and Gitter, 2020; Shen, 2015]. )

b) Non-linear Dynamics Tackled by Koopman Theory

Koopman theory [Koopman, 1931; Brunton et al., 2022]

• linear dynamical system can be represented as an infinite-dimensional non-linear Koopman operator \(\mathcal{K}\)

• which operates on a space of measurement functions \(g\), such that..

  \(\mathcal{K} \circ g\left(x_t\right)=g\left(\mathbf{F}\left(x_t\right)\right)=g\left(x_{t+1}\right)\).

Dynamic Mode Decomposition(DMD) [Schmid and Sesterhenn, 2008]

• seeks the best fitted matrix \(K\) to approximate infinite-dimensional operator \(\mathcal{K}\) by collecting the observed system states
• Limitation: highly nontrivial to find appropriate measurement functions \(g\) as well as the Koopman operator \(\mathcal{K}\).

Koopman theory serves as a connection between ..

• finite-dimensional nonlinear dynamics
• infinite-dimensional linear dynamics

Proposal: KTD module (to tackle nonlinear dynamics)

• Consider TS data \(\mathbf{X}=\left\{\mathbf{x}_1, \ldots, \mathbf{x}_T\right\}\) as observations of a series of dynamic system states,
  • where \(\mathbf{x}_i \in \mathbb{R}^N\) is the system state.

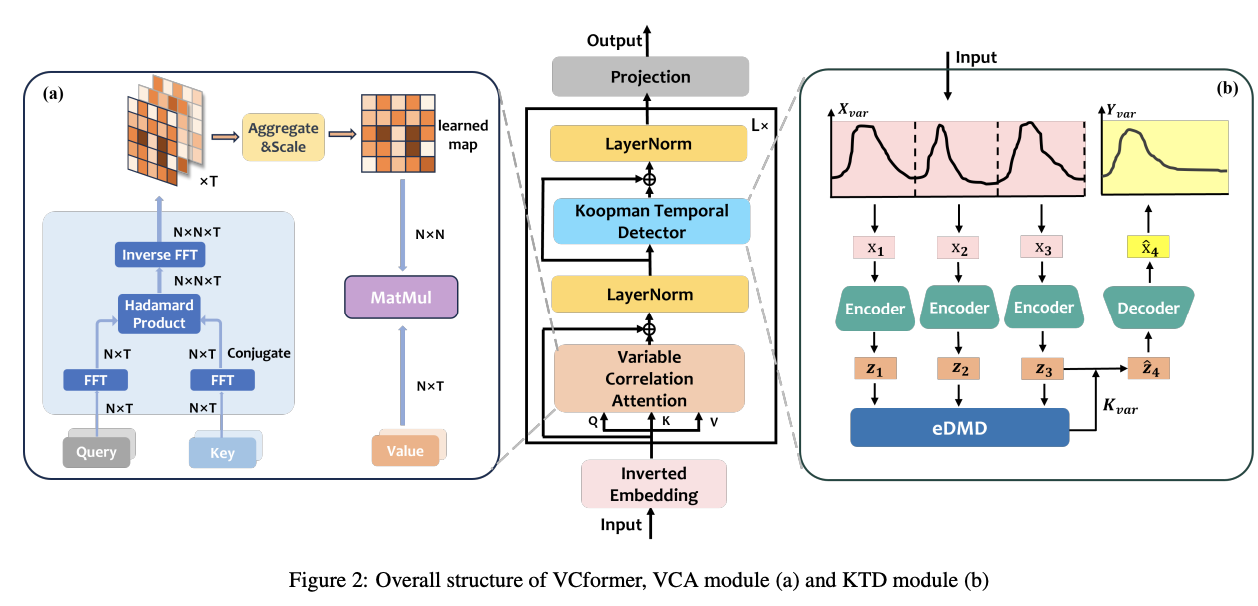
(2) Structure Overview

[1] Following the same Encoder-only structure as iTransformer

\(\rightarrow\) Adopt the Inverted Embedding : \(\mathbb{R}^T \mapsto \mathbb{R}^D\),

• which regards each UTS as the embedded token

[2] Stacking \(L\) layers with VCA and KTD modules

• [VCA] cross-variable relationships
• [KTD] temporal dependencies

[3] Final prediction (by the Projection) \(: \mathbb{R}^D \mapsto \mathbb{R}^H\).

(3) Variable Correlation Attention

a) Lagged Cross-correlation Computing

Stochastic process theory [Chatfield and Xing, 2019]

• Real discrete-time process \(\left\{\mathcal{X}_t\right\}\),
• Autocorrelation \(R_{\mathcal{X}, \mathcal{X}}(\tau)\)
  • \(R_{\mathcal{X}, \mathcal{X}}(\tau)=\lim _{L \rightarrow \infty} \frac{1}{L} \sum_{\tau=1}^L \mathcal{X}_t \mathcal{X}_{t-\tau}\).

Approximation for the autocorrelation of variates \(i\) :

• \(R_{\mathbf{q}_i, \mathbf{k}_i}(\tau)=\sum_{\tau=1}^T\left(\mathbf{q}_i\right)_t \cdot\left(\mathbf{k}_i\right)_{t-\tau}=\mathbf{q}_i \odot \operatorname{ROLL}\left(\mathbf{k}_i, \tau\right)\).
  • queries \(Q=\left[\mathbf{q}_1, \mathbf{q}_2, \ldots, \mathbf{q}_N\right]\)
  • keys \(K=\) \(\left[\mathbf{k}_1, \mathbf{k}_2, \ldots, \mathbf{k}_N\right]\)
    • where \(\mathbf{q}_i, \mathbf{k}_j \in \mathbb{R}^{T \times 1}\),
  • \(\operatorname{ROLL}\left(\mathbf{k}_i, \tau\right)\): elements of \(\mathbf{k}_i\) shift along the time dimension

This idea was also harnessed in Autoformer [Wu et al., 2021].

Similarly, we can compute the cross-correlation between variate \(i\) and \(j\) by

• \(\text { LAGGED-COR }\left(\mathbf{q}_i, \mathbf{k}_j\right)=\mathbf{q}_i \odot \operatorname{ROLL}\left(\mathbf{k}_j, \tau\right)\).

b) Scores Aggregation

Total correlation of variate \(i\) and \(j\),

= Aggregate different lags \(\tau\) from 1 to \(T\)

( with learnable parameters \(\lambda=\) \(\left[\lambda_1, \lambda_2, \ldots, \lambda_T\right]\) )

• \(\operatorname{COR}\left(\mathbf{q}_i, \mathbf{k}_j\right)=\sum_{\tau=1}^T \lambda_i R_{\mathbf{q}_i, \mathbf{k}_j}(\tau)\).

VCA performs softmax on the learned multivariate correlation map \(\mathbf{A} \in \mathbb{R}^{N \times N}\) at each row and obtains the output via …

• \(\operatorname{VCA}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{SOFTMAX}(\operatorname{COR}(\mathbf{Q}, \mathbf{K})) \mathbf{V}\).

(4) Koopman Temporal Detector (KTD)

Pass

(5) Efficient Computation

Pass