(paper) A benchmark study on time series clustering

A benchmark study on time series clustering (2020)

Contents

1. Abstract
2. Introduction
3. Benchmark methods
   1. Clustering methods
   2. Evaluation methods

0. Abstract

8 popular clustering methods ( of 3 categories )

• 1) partitional
• 2) hierarchical
• 3) density-based

3 types of distance measures

• 1) Euclidean
• 2) DTW (Dynamic Time Warping)
• 3) shape-based

1. Introduction

data : UCR(University of California) time series

• 128 datasets
• split into train/test
• accompanied by 3 baseline straw man classification accuracy scores

2. Benchmark methods

(1) Clustering methods

2 major design criteria in clustering methods

• 1) clustering algorithm
• 2) distance measure

a) clustering algorithm

• [1] partitional
  • ex) K-means, K-medoids, Fuzzy C-means
• [2] density-based
  • ex) Density Peaks (2019)
    • recent popularity, particularly for TS clustering
    • not sensitive to density parameter
    • needs the number of cluster \(k\) in advance
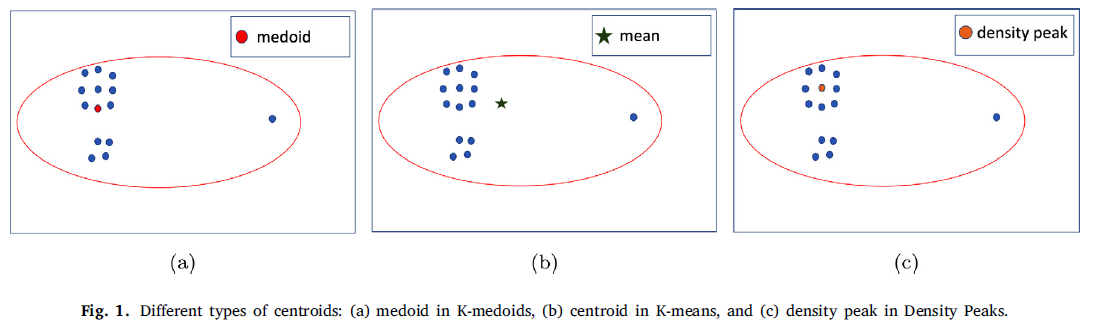
    • 2 phases
      • step 1) find centroids ( =density peaks )
      • step 2) assign data points to closes centroid
    • 2 input params :
      • number of clusters (\(k\))
      • local neighborhood distance (\(d\))
• [3] hierarchical
  • agglomerative (bottom-up) / divisive (top-down)

b) distance measure

• [1] Euclidean
  • two time series \(T 1=\left(T 1_{1}, T 1_{2}, \ldots, T 1_{n}\right)\) and \(T 2=\left(T 2_{1}, T 2_{2}, \ldots, T 2_{n}\right)\)
  • \(d(T 1, T 2)=\sqrt{\sum_{i}^{n}\left(T 1_{i}-T 2_{i}\right)^{2}}\).
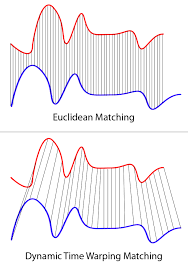
• [2] Dynamic time warping
  • mapping of points between a pair of time series, \(T_1\) & \(T_2\)
  • designed to minimize pairwise Euclidean distance
  • one of most accurate SIMILARITY measures for ts data
• [3] Shape-based distance
  • shift-invariant & scale-invariant
  • calculates cross-correlation between 2 t.s data
  • value between 0.0~2.0
    • 0.0 : identical
    • 2.0 : maximally different shape
  • to ensure scale-invariance…
    • normalize! \(T^{\prime}=\frac{T-\mu}{\sigma}\).

(2) Evaluation methods

metrics for assessing clustering : (1) external & (2) internal

• [1] external : with class labels
  • ex) RI, ARI, AMI, FMS…
• [2] internal : without class labels
  • ex) Silhouette score, Davies-Bouldin index, Calinski-Harabasz index…