Deep MTS Embedding Clustering via Attentive-Gated Autoencoder (2020)
Contents
- Abstract
- Introduction
- DeTSEC : Deep Time Series Embedding Clustering
0. Abstract
propose a DL-based framework for clustering MTS, with varying length
\(\rightarrow\) propose DeTSEC (Deep Time Series Embedding Clustering)
1. Introduction
DeTSEC (Deep Time Series Embedding Clustering)
- different domains OK
- varying length OK
2 stages
- step 1) Recurrent autoencoder exploits attention & gating mechanism to produce a preliminary embedding representation
- step 2) Clustering Refinement stage
- stretch the embedding manifold towards the corresponding cluters
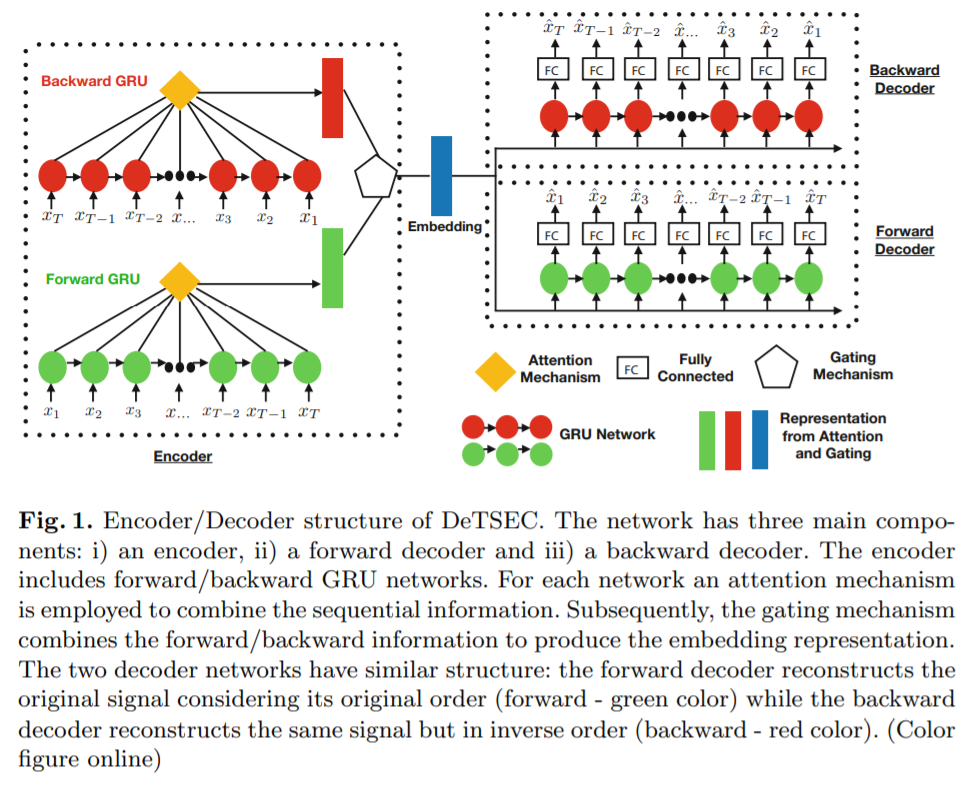
2. DeTSEC : Deep Time Series Embedding Clustering
Notation
-
\(X=\left\{X_{i}\right\}_{i=1}^{n}\) : multivariate time-series
-
\(X_{i} \in X\) : time-series
where \(X_{i j} \in R^{d}\) = multidimensional vector of the time-series \(X_{i}\) at timestamp \(j\), with \(1 \leq j \leq T\)
-
\(d\) : dimensionality of \(X_{i j}\)
-
\(T\) : maximum time-series length
-
-
\(X\) can contain time-series with DIFFERENT length
Goal
- partition \(X\) in a given number of clusters
2 stages
-
stage 1) GRU based autoencoder
-
for each GRU unit, attention is applied,
to combine the information coming from different timestamps
-
-
stage 2) refine the representation, by taking into account a 2-fold task
- 1) reconstruction
- 2) another one devoted to stretch the embedding manifold towards clustering centroids
3 different compontents
- 1) encoder
- 2-1) backward decoder
- 2-2) forward decoder
Loss Function
(1) autoencoder network
\(\begin{aligned} L_{a e}=& \frac{1}{ \mid X \mid } \sum_{i=1}^{ \mid X \mid } \mid \mid X_{i}-\operatorname{dec}\left(\operatorname{enc}\left(X_{i}, \Theta_{1}\right), \Theta_{2}\right) \mid \mid _{2}^{2} \\ &+\frac{1}{ \mid X \mid } \sum_{i=1}^{ \mid X \mid } \mid \mid \operatorname{rev}\left(X_{i}\right)-\operatorname{dec}_{b a c k}\left(\operatorname{enc}\left(X_{i}, \Theta_{1}\right), \Theta_{3}\right) \mid \mid _{2}^{2} \end{aligned}\).
(2) regularizer term
\(\frac{1}{ \mid X \mid } \sum_{i=1}^{ \mid X \mid } \sum_{l=1}^{n C l u s t} \delta_{i l} \mid \mid \text { Centroids }_{l}-\operatorname{enc}\left(X_{i}, \Theta_{1}\right) \mid \mid _{2}^{2}\).
(3) Total loss : (1) + (2)
