(paper) Informer ; Beyond Efficient Transformer for Long Sequence Time-Series Forecasting

Informer ; Beyond Efficient Transformer for Long Sequence Time-Series Forecasting (2021)

Contents

1. Abstract
2. Introduction
3. Preliminary
   1. LSTF problem definition
   2. Encoder-decoder architecture
4. Methodology
   1. Efficient self-attention mechanism
   2. Encoder
   3. Decoder

0. Abstract

많은 real world problem : LONG sequence time-series 예측을 필요로 함

\(\rightarrow\) LSTF (LONG sequence time-series forecasting)

• 그러기 위해, need to capture precise “LONG-range dependency” coupling between input & output

그러는데에 있어서 역시 최고는 TRANSFORMER!

하지만, Transformer의 문제점?

• 1) quadratic time complexity
• 2) high memory usage
• 3) inherent limitation of encoder-decoder architecture

이 문제들을 극복하기 위해, “Informer”를 제안함

( = efficient transformer-based model for LSTF )

Informer의 3가지 특징

• (1) ProbSparse self-attention mechanism
  • time complexity & memory usage : \(O(L \log L)\)
• (2) self-attention distilling highlights dominating attention by halving
• (3) generative style decoder

1. Introduction

LSTF (Long sequence time-series forecasting) 풀기!

( 대부분의 기존 work들은 short-term… )

아래 그림은 LSTM을 사용하여 short & long term을 예측한 결과!

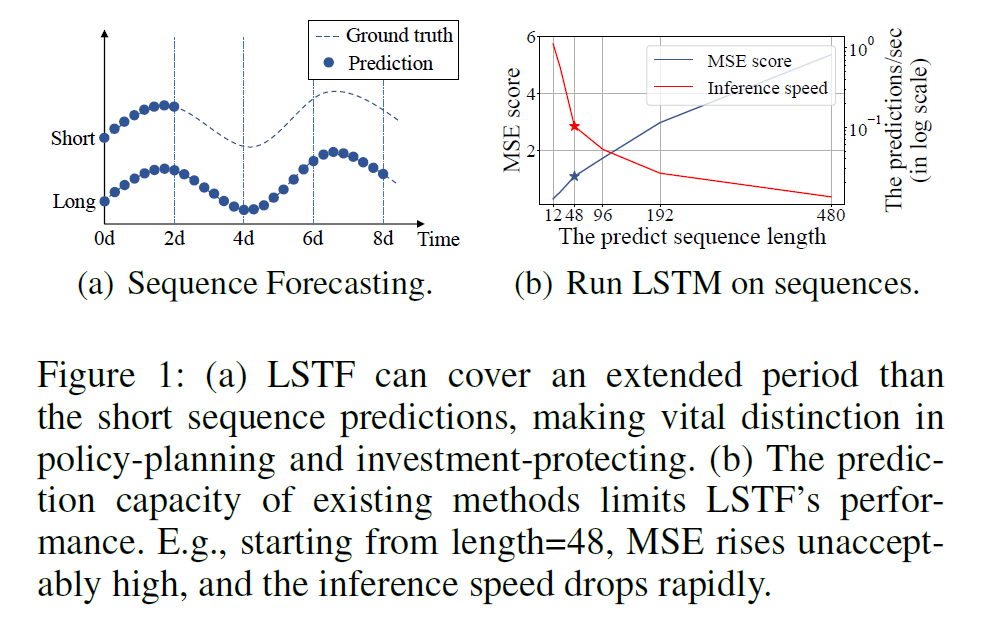
Challenge of LSTF

long-sequence에서도 잘 예측해야하는게 매우 hard! 그러기 위해…

• 요건 1) extraordinary long-range alignment ability
• 요건 2) efficient operations on long sequence input&output

\(\rightarrow\) 이 요건 2) 가 Transformer를 사용하는데에 있어서 문제점!

우리는 이 Transformer을 보다 efficient하게 만들 수 없을까?

Limitations of Transformer

• 한계 1) Quadratic computation of self-attention
• 한계 2) Memory bottleneck in stacking layers for long inputs
• 한계 3) Speed Plunge in predicting long outputs

한계 1)을 풀기 위해 나왔던 기존의 연구들

• Sparse Transformer / LogSparse Transformer / Longformer / Reformer / Linformer / Transformer-XL / Compressive Transformer …

한계 2&3)을 풀기 위해 나왔던 연구들은 없다!

• 이게 바로 “Informer”가 풀고자 했던 것! ( 한계 1)은 물론이고 )

Contributions

• 1) Propose Informer to successfully enhance prediction capacity in LSTF problems

• 2) Propose ProbSparse self-attention for efficiency
• 3) Propose self-attention distilling operation to privilege dominating attention scores
• 4) Propose generative style decoder to acquire long sequence output with only one forward step

2. Preliminary

(1) LSTF problem definition

Input : (at time \(t\) )

• \(\mathcal{X}^{t}=\left\{\mathbf{x}_{1}^{t}, \ldots, \mathbf{x}_{L_{x}}^{t} \mid \mathbf{x}_{i}^{t} \in \mathbb{R}^{d_{x}}\right\}\).

Output :

• \(\left\{\mathbf{y}_{1}^{t}, \ldots, \mathbf{y}_{L_{y}}^{t} \mid \mathbf{y}_{i}^{t} \in \mathbb{R}^{d_{y}}\right\} .\).

LSTF problem = LONG = \(L_{y}\) 가 크다

Univariate이 아닌 Multivariate case : \(\left(d_{y} \geq 2\right)\)

(2) Encoder-decoder architecture

위 문제를 풀기 위한 DL은 주로 Encoder-decoder 구조를 가진다

• Encode : \(\mathcal{X}^{t}\) \(\rightarrow\) \(\mathcal{H}^{t}=\left\{\mathbf{h}_{1}^{t}, \ldots, -\mathbf{h}_{L_{h}}^{t}\right\}\)

• Decode : \(\mathcal{H}^{t}=\left\{\mathbf{h}_{1}^{t}, \ldots, \mathbf{h}_{L_{h}}^{t}\right\}\) \(\rightarrow\) \(\mathcal{Y}^{t}\)

Inference step : “dynamic decoding”

• 1) decoder computes a \(\mathbf{h}_{k+1}^{t}\) from \(\mathbf{h}_{k}^{t}\) & other necessary outputs from \(k\) -th step )
• 2) predict the \((k+1)\) -th sequence \(\mathbf{y}_{k+1}^{t}\) using \(\mathbf{h}_{k+1}^{t}\)

3. Methodology

제안한 Informer

• encoder-decoder 구조를 가지면서
• LSTF 문제를 풀고자함

(1) Efficient self-attention mechanism

일반적인 attention

• \(\mathcal{A}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{Softmax}\left(\mathrm{QK}^{\top} / \sqrt{d}\right) \mathbf{V}\).

\(i\) -th query’s attention

• \(\mathcal{A}\left(\mathbf{q}_{i}, \mathbf{K}, \mathbf{V}\right)=\sum_{j} \frac{k\left(\mathbf{q}_{i}, \mathbf{k}_{j}\right)}{\sum_{l} k\left(\mathbf{q}_{i}, \mathbf{k}_{l}\right)} \mathbf{v}_{j}=\mathbb{E}_{p\left(\mathbf{k}_{j} \mid \mathbf{q}_{i}\right)}\left[\mathbf{v}_{j}\right]\).
  • where \(p\left(\mathbf{k}_{j} \mid \mathbf{q}_{i}\right)=k\left(\mathbf{q}_{i}, \mathbf{k}_{j}\right) / \sum_{l} k\left(\mathbf{q}_{i}, \mathbf{k}_{l}\right)\).
• requires the quadratic times dot-product computation and \(\mathcal{O}\left(L_{Q} L_{K}\right)\) memory usage

\(\rightarrow\)“SPARSITY” self-attention score 사용의 필요성!

Query Sparsity Measurement

Dominant dot-product pair = Uniform 분포와 차이가 클 것!

( \(q\left(\mathrm{k}_{j} \mid \mathrm{q}_{i}\right)=1 / L_{K}\) )

\(\rightarrow\) KL-divergence로 이를 측정

\(K L(q \| p)=\ln \sum_{l=1}^{L_{K}} e^{\mathbf{q}_{i} \mathbf{k}_{l}^{\top} / \sqrt{d}}-\frac{1}{L_{K}} \sum_{j=1}^{L_{K}} \mathbf{q}_{i} \mathbf{k}_{j}^{\top} / \sqrt{d}-\ln L_{K}\).

상수 부분 버리면, \(i\)-th query’s sparsity measurement는 :

\(M\left(\mathbf{q}_{i}, \mathbf{K}\right)=\ln \sum_{j=1}^{L_{K}} e^{\frac{\mathbf{a}_{i} \mathbf{k}_{j}^{\top}}{\sqrt{d}}}-\frac{1}{L_{K}} \sum_{j=1}^{L_{K}} \frac{\mathbf{q}_{i} \mathbf{k}_{j}^{\top}}{\sqrt{d}}\).

직관적 의미

• \(M\left(\mathbf{q}_{i}, \mathbf{K}\right)\) 가 크다
• \(p\) 가 diverse하다
• dominate dot-product pairs를 가질 가능성이 높다

ProbSparse Self-attention

상위 \(u\)개의 dominant query만을 사용!

\(\mathcal{A}(\mathbf{Q}, \mathbf{K}, \mathbf{V})=\operatorname{Softmax}\left(\frac{\overline{\mathbf{Q}} \mathbf{K}^{\top}}{\sqrt{d}}\right) \mathbf{V}\).

• \(M(\mathbf{q}, \mathbf{K})\) 가 높은 Top-\(u\) query만을 사용한 \(\overline{\mathrm{Q}}\)

(2) Encoder

key : Allowing for Processing Longer Sequential Inputs under the Memory Usage Limitation

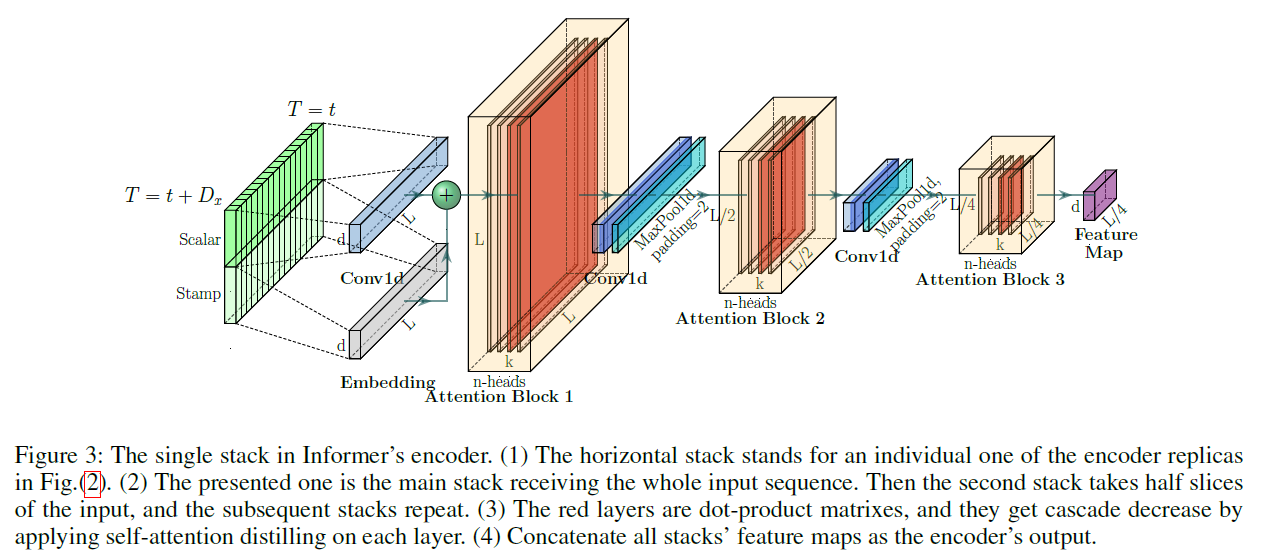
• extract robust “long-range” dependency of long sequential inputs
• input : \(\mathbf{X}_{\text {en }}^{t} \in \mathbb{R}^{L_{x} \times d_{\text {model }}}\).

Self-attention Distilling

encoder’s feature map has “redundant” combinations of value \(\mathbf{V}\)

\(\rightarrow\) distilling operation to privilege the superior ones

( = make a focused self-attention )

\(\mathbf{X}_{j+1}^{t}=\) MaxPool \(\left(\operatorname{ELU}\left(\operatorname{Conv} 1 \mathrm{~d}\left(\left[\mathbf{X}_{j}^{t}\right]_{\mathrm{AB}}\right)\right)\right)\).

• 1-D convolutional filters (kernel width=3) o
• max-pooling layer with stride 2
• downsample \(\mathbf{X}^{t}\) into its half slice after stacking a layer

\(\rightarrow\) reduces the whole memory usage to be \(\mathcal{O}((2-\epsilon) L \log L)\)

(3) Decoder

key : Generating Long Sequential Outputs Through One Forward Procedure

• composed of stack of 2 identical multi-head attention layers

• feed decoder with…

  \(\mathbf{X}_{\mathrm{de}}^{t}=\operatorname{Concat}\left(\mathbf{X}_{\text {token }}^{t}, \mathbf{X}_{0}^{t}\right) \in \mathbb{R}^{\left(L_{\text {token }}+L_{y}\right) \times d_{\text {model }}}\).

  • \(\mathbf{X}_{\text {token }}^{t} \in \mathbb{R}^{L_{\text {token }} \times d_{\text {model }}}\) : start token
  • \(\mathbb{R}^{L_{y} \times d_{\text {model }}}\) : target sequence (set scalar as 0)

• “Masked” multi-head attention in ProbSparse self-attention

  • avoids auto-regressive

Generative Inference

• dynamic decoding

• instead of choosing specific flags as the token….

  sample \(L_{tkoen}\) long sequence in the input sequence

  ( ex. earlier slice before the output sequence )

• example)

  • 미래의 168 point ( = 7일 x 24시 ) 예측하고 싶음

  • 예측 시작 시점의 앞선 5일을 start token으로써 사용하기

    \(\mathbf{X}_{\mathrm{de}}=\left\{\mathbf{X}_{5 d}, \mathbf{X}_{0}\right\}\).

Loss Function = MSE