(paper) Learning Representations for Time Series Clustering

Learning Representations for Time Series Clustering (2019)

Contents

1. Abstract
2. Introduction
3. Related Works
   1. raw-data-based methods
   2. feature-based methods
4. DTCR (Deep Temporal Clustering Representation)
   1. Deep Temporal Representation Clustering
   2. Encoder Classification task
   3. Overall Loss Function
   4. Pseudo-code

0. Abstract

TS clustering : essential, when category information is not available

propose a novel unsupervised temporal representation learning model, called..

• DTCR (Deep Temporal Clustering Representation)

DTCR

• integrates “(1) temporal reconstruction” & “(2) K-means objective” into seq2seq
• obtain cluster-specific temporal representations

1. Introduction

Feature-based methods

• extracted features & clusters
• robust to noise & filter out irrelevant information
• reduce data dimension & improve efficiency
• BUT, most are domain-dependent

Deep Learning models

• seq2seq

  • learn general representations from sequence data in unsupervised manner

• [THIS PAPER]

  • aim to learn a non-linear temporal representation for time-series clustering, using seq2seq

  • relies on the capabilities of encoder

Propose DTCR (Deep Temporal Clustering Representation)

• 1) generate CLUSTER-SPECIFIC temporal representations
• 2) integrates “(1) temporal reconstruction” & “(2) K-means objective” into seq2seq
• 3) adapts bidirectional Dilated RNN as encoder

2. Related Works

time series clustering

• 1) raw-data-based methods
• 2) feature-based methods

(1) raw-data-based methods

• mainly modify distance function

• ex) k-DBA ( = K-means + DTW )

• ex) k-SC ( K-Spectral Centroid )

  • uncover the temporal dynamics, using similarity metric that is invariant to scaling/shifting

• ex) k-Shape

  • considers the shapes of time series
  • using a normalized version of cross-correlation measure

• above are sensitive to outliers & noise

  ( \(\because\) all time points are taken into account )

(2) feature-based methods

• 1) mitigates the impact of noise / outliers
• 2) reduce dimensionality
• divide feature-based methods into
  • (1) two-stage approaches : extract features \(\rightarrow\) clustering
  • (2) jointly optimize

DTC (Deep Temporal Clustering)

• use “auto encoder” & “clustering layer”
• learn non-linear cluster representation
• clustering layer : designed by measuring KL-divergence between predicted & target distn

3. DTCR (Deep Temporal Clustering Representation)

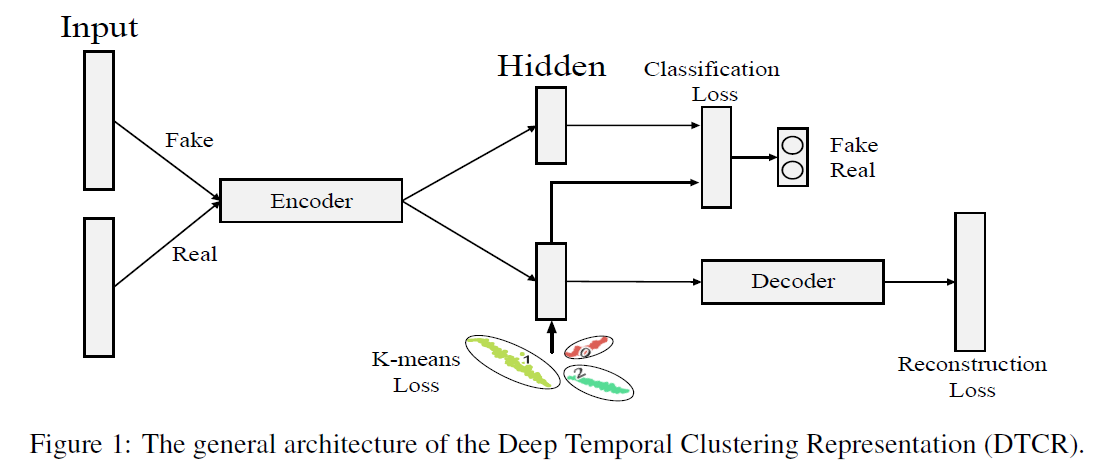
Summary

• (1) [ENCODER] raw time series \(\rightarrow\) latent space of representation

• (2) [DECODER] representations \(\rightarrow\) reconstruct input

  ( + K-means objective is integrated….to guide representation learning )

• propose fake-sample generation & auxiliary classification task to enhance encoder

(1) Deep Temporal Representation Clustering

Notation

• \(n\) : number of time series ( \(n>1\) : MTS )
• \(D=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}\).
  • each time series \(x_{i}\) : contains \(T\) ordered real values
  • \(\boldsymbol{x}_{\boldsymbol{i}}=\left(x_{i, 1}, x_{i, 2}, \ldots x_{i, T}\right)\).
• encoder & decoder
  • \(f_{\text {enc }}: \boldsymbol{x}_{\boldsymbol{i}} \rightarrow \boldsymbol{h}_{\boldsymbol{i}}\).
  • \(f_{\text {dec }}: h_{i} \rightarrow \hat{x}_{i}\).
• \(m\)-dim latent representation : \(h_{i} \in \mathbb{R}^{m}\).
  • \(h_{i}=f_{\text {enc }}\left(x_{i}\right)\).
• decoded output :
  • \(\hat{\boldsymbol{x}}_{\boldsymbol{i}}=f_{\text {dec }}\left(\boldsymbol{h}_{\boldsymbol{i}}\right)\).

Reconstruction Loss : MSE

• \(\mathcal{L}_{\text {reconstruction }}=\frac{1}{n} \sum_{i=1}^{n} \mid \mid \boldsymbol{x}_{\boldsymbol{i}}-\hat{\boldsymbol{x}_{\boldsymbol{i}}} \mid \mid _{2}^{2}\).

• not sufficient!

  ( not suitable for clustering task )

K-means Objective

• \(\mathcal{L}_{K-\text { means }}=\operatorname{Tr}\left(\boldsymbol{H}^{\boldsymbol{T}} \boldsymbol{H}\right)-\operatorname{Tr}\left(\boldsymbol{F}^{\boldsymbol{T}} \boldsymbol{H}^{\boldsymbol{T}} \boldsymbol{H} \boldsymbol{F}\right)\).
  • minimization of \(\mathrm{K}\)-means = trace maximization problem associated with the Gram matrix \(\boldsymbol{H}^{T} \boldsymbol{H}\)
  • static data matrix \(\boldsymbol{H} \in \mathbb{R}^{m \times N}\)
  • \(\boldsymbol{F} \in \mathbb{R}^{N \times k}\) is the cluster indicator matrix.
• use as regularization term

Final Objective

\(\min _{\boldsymbol{H}, \boldsymbol{F}} J(\boldsymbol{H})+\frac{\lambda}{2}\left[\operatorname{Tr}\left(\boldsymbol{H}^{\boldsymbol{T}} \boldsymbol{H}\right)-\operatorname{Tr}\left(\boldsymbol{F}^{\boldsymbol{T}} \boldsymbol{H}^{\boldsymbol{T}} \boldsymbol{H} \boldsymbol{F}\right)\right], \text { s.t. } \boldsymbol{F}^{\boldsymbol{T}} \boldsymbol{F}=\boldsymbol{I}\).

• \(J(\boldsymbol{H})\) : 1) + 2)
  • 1) reconstruction loss
  • 2) classification loss

(2) Encoder Classification task

better encoder = better representation

\(\rightarrow\) propose a fake-sample generation strategy & auxiliary classification task

fake-sample generation

• generate its fake version by randomly shuffling some time steps

• number of selected time steps = \(\lfloor\alpha \times T\rfloor\)

  ( where \(\alpha \in(0,1]\) is a hyper-parameter we set to \(0.2\) )

auxiliary classification task

• train the encoder to detect whether a given time series is REAL or FAKE

• trained by minimizing …

  \(\mathcal{L}_{\text {classification }}=-\frac{1}{2 N} \sum_{i=1}^{2 N} \sum_{j=1}^{2} 1\left\{y_{i, j}=1\right\} \log \frac{\exp \hat{y}_{i, j}}{\sum_{j=1}^{2} \exp \left(\hat{y}_{i, j}\right)}\).

  where \(\hat{y}_{i}=W_{f c 2}\left(\boldsymbol{W}_{f c 1} h_{i}\right)\).

  • \(y_{i}\) : 2-dim one-hot vector ( = answer )
  • \(\hat{y}_{i}\) : classification result
  • \(\boldsymbol{W}_{f c 1} \in \mathbb{R}^{m \times d}, \boldsymbol{W}_{f c 2} \in \mathbb{R}^{d \times 2}\).

(3) Overall Loss Function

\(\mathcal{L}_{D T C R}=\mathcal{L}_{\text {reconstruction }}+\mathcal{L}_{\text {classification }}+\lambda \mathcal{L}_{K-\text { means }}\).

(4) Pseudo-code