(paper) Neural Basis Expansion analysis with exogenous variables ; Forecasting electricity prices with NBEATSx

Neural Basis Expansion analysis with exogenous variables ; Forecasting electricity prices with NBEATSx (2021)

Contents

1. Abstract
2. Introduction
3. Literature Review
   1. DL & Sequence Modeling
   2. Electricity Price Forecasting (EPF)
4. NBEATSx Model
   1. Stacks and Blocks
   2. Residual Connections

0. Abstract

neural basis expansion analysis (NBEATS) to incorporate exogenous factors

• extend its capabilities by including “exogenous variables”

1. Introduction

DL for forecasting tasks … example )

• ESRNN (Exponential Smoothing Recurrent Neural Network)
• NBEATS (Neural Basis Expansion Analysis)

Still, 2 possible improvements!

• 1) integration of time-dependent exogenous variables
• 2) interpretability of NN outputs

2. Literature Review

(1) DL & Sequence Modeling

a) basic models

• RNN, LSTM, GRU

b) adoptions of Conv & Skip-connection within RNN

• WaveNet
• Dilated RNN (DRNN)
• Temporal Convolutional Network (TCN)

c) Seq2Seq

• better forecasting performance than classical statistical methods

(2) Electricity Price Forecasting (EPF)

EPF task : predicting the spot & forward prices in the market

• mostly focus on predicting “24 hours of the next day”
  • either at “point” or “probabilistic” setting
• majority of NN solving EPF suffer…
  • too short/limited to ONE market test period

3. NBEATSx Model

decomposes the object signal by performing separate local nonlinear projection of the target data onto basis functions across its different blocks

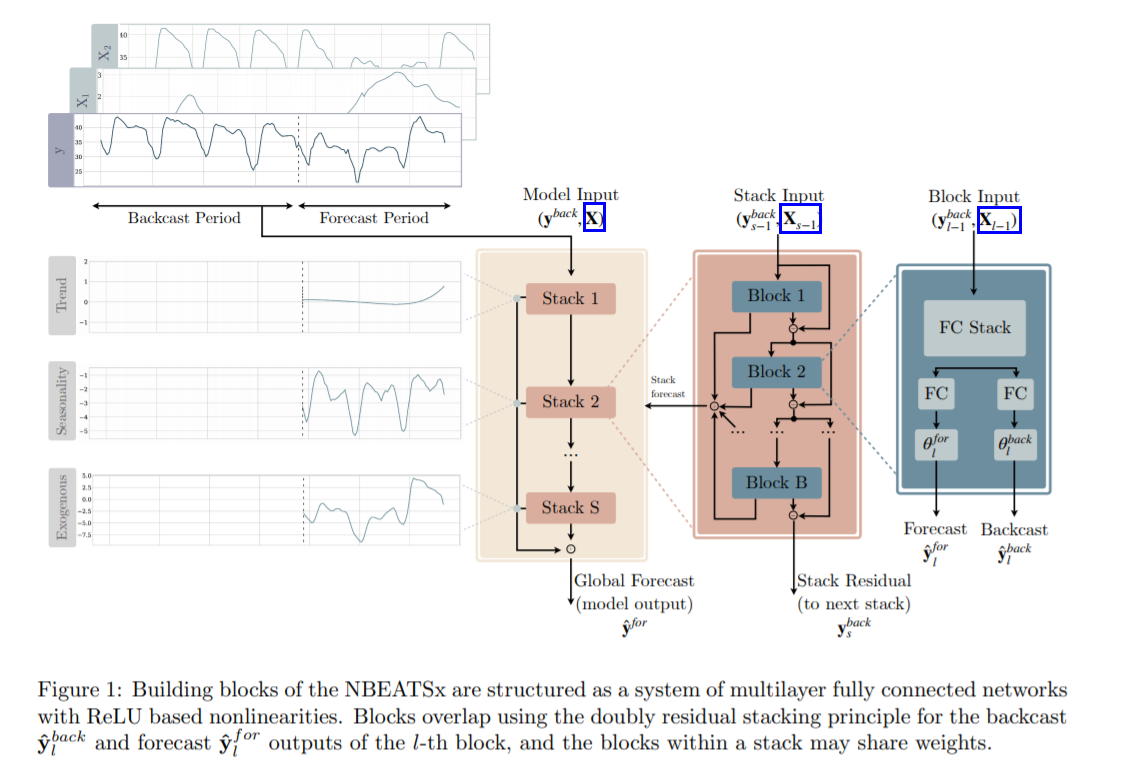
• each block consists of FCNN, which learns expansion coefficients for back&forecast
  • backcast : used to clean the inputs of subsequent blocks
  • forecast : summed to compose the final prediction

• notation

  • objective signal : \(\mathbf{y}\)

  • inputs for the model = 1) + 2)

    • 1) backcast window vector \(\mathbf{y}^{\text {back }}\) of length \(L\)

      ( \(L\) = length of the lags )

    • 2) forecast window vector \(\mathbf{y}^{\text {for }}\) of length \(H\)

      ( \(H\) = forecast horizon )

• original NBEATS : admits \(\mathbf{y}^{\text {back }}\)

  NBEATSx : admits \(\mathbf{y}^{\text {back }}\) & \(\mathbf{X}\) ( =exogenous matrix )

(1) Stacks and Blocks

NBEATSx is composed by S stacks of B blocks

( first transformation )

\(\mathbf{h}_{l} =\mathbf{F C N N}_{l}\left(\mathbf{y}_{l-1}^{b a c k}, \mathbf{X}_{l-1}\right)\).

• \(\boldsymbol{\theta}_{l}^{f o r} =\mathbf{L I N E A R}^{f o r}\left(\mathbf{h}_{l}\right)\).
• \(\boldsymbol{\theta}_{l}^{\text {back }}=\mathbf{L I N E A R}^{\text {back }}\left(\mathbf{h}_{l}\right)\).

( second transformation )

\(\hat{\mathbf{y}}_{l}^{b a c k}=\sum_{i=1}^{ \mid \theta_{l}^{b c k} \mid } \theta_{l, i}^{\text {back }} \mathbf{v}_{l, i}^{\text {back }} \equiv \boldsymbol{\theta}_{l}^{\text {back }} \mathbf{V}_{l}^{\text {back }}\).

\(\hat{\mathbf{y}}_{l}^{f o r}=\sum_{i=1}^{ \mid \boldsymbol{\theta}_{l}^{\text {for}} \mid } \theta_{l, i}^{\text {for }} \mathbf{v}_{l, i}^{f o r} \equiv \boldsymbol{\theta}_{l}^{\text {for }} \mathbf{V}_{l}^{\text {for }}\).

• block’s basis vectors : \(\mathbf{V}_{l}^{\text {back }}\) & \(\mathbf{V}_{l}^{\text {for}}\)

(2) Residual Connections

connections between blocks :

• \(\mathbf{y}_{l}^{\text {back }}=\mathbf{y}_{l-1}^{\text {back }}-\hat{\mathbf{y}}_{l-1}^{\text {back }}\).
• \(\hat{\mathbf{y}}^{\text {for }}=\sum_{l=1}^{S \times B} \hat{\mathbf{y}}_{l}^{\text {for }}\).

이하는 NBEATS와 동일하므로 생략