Precursor-of-Anomaly Detection for Irregular Time Series

Precursor-of-Anomaly Detection for Irregular Time Series

https://arxiv.org/pdf/2306.15489

Contents

1. Abstract
2. Introduciton
3. Preliminaries
4. Proposed Methods
   1. Problem statement
   2. Overall workflow
   3. NN based on co-evolving NCDEs
   4. Training algorithm
5. Experiments
   1. Regular TS
   2. Irregular TS

Abstract

Precursor-of-Anomaly (PoA) detection.

• Propose a novel type of AD

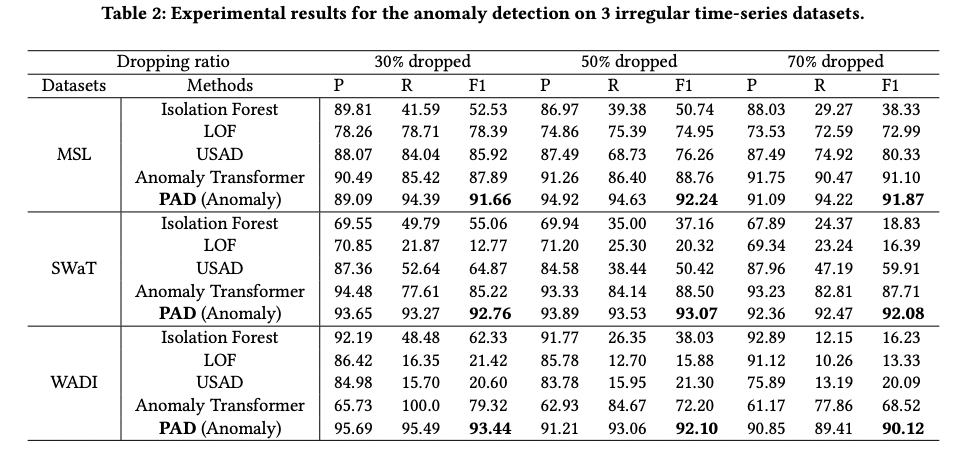
(Conventional) AD vs. PoA

• (Conventional) AD: Focuses on determining whether a **GIVEN time series ** is anomaly
• PoA: Focuses on determining whether a **FUTURE time series ** is anomaly

Proposed algorithm: Neural controlled differential equation-based NN

1. Introduction

Contributions

1. First to solve both AD & PoA
2. Propose PAD (NCDE-based unified framework)
3. Design a (1) multi-task & (2) knowledge distillation learning method

4. Self-supervised learning (SSL)

5. Propose an augmentation method to create artificial anomalies for SSL
6. Regular & Irregular TS experiments + Code provided
   • https://github.com/sheoyon-jhin/PAD

2. Preliminaries

Differential equations

• Neural Ordinary Differential Equations (NODE)
• Neural Controlled Differential Equations (NCDE)

NODE vs. NCDE

• NODE:
  • \(\mathbf{z}(T)=\mathbf{z}(0)+\int_0^T f\left(\mathbf{z}(t), t ; \theta_f\right) d t\).
• NCDE:
  • \(\begin{aligned} z(T) & =z(0)+\int_0^T f\left(z(t) ; \theta_f\right) d X(t) \\ & =z(0)+\int_0^T f\left(z(t) ; \theta_f\right) \frac{d X(t)}{d t} d t \end{aligned}\).

3. Proposed Methods

(1) Problem statement

Notation & Settings

• MTS: \(\mathbf{x}_{0: T}=\left\{\mathbf{x}_0, \mathbf{x}_1, \ldots, \mathbf{x}_T\right\}\), where., \(\mathbf{x}_t \in \mathbb{R}^N\).
  • (Irregular TS) Time-interval between two consecutive observations is not a constant
  • (Regular TS) Time0interval is fixed
• Window-based approach
  • \(x_{0:T}\) is divided into non-overlapping windows
    • i.e., \(w_i=\) \(\left[\mathbf{x}_{t_0^l}, \mathbf{x}_{t_i^l}, \ldots, \mathbf{x}_{t_b^l}\right]\) where \(t_j^i=i \times b+j-1\) with a window size of \(b\).
    • \(\left\lceil\frac{T}{b}\right\rceil\) windows in total for \(x_{0, T}\).

Task: For a given input window \(w_i\), …

• (AD) Decides whether \(w_i\) contains abnormal observations
• (PoA) Decides whether \(w_{i+1}\) contains abnormal observations

(Both are binary classification tasks)

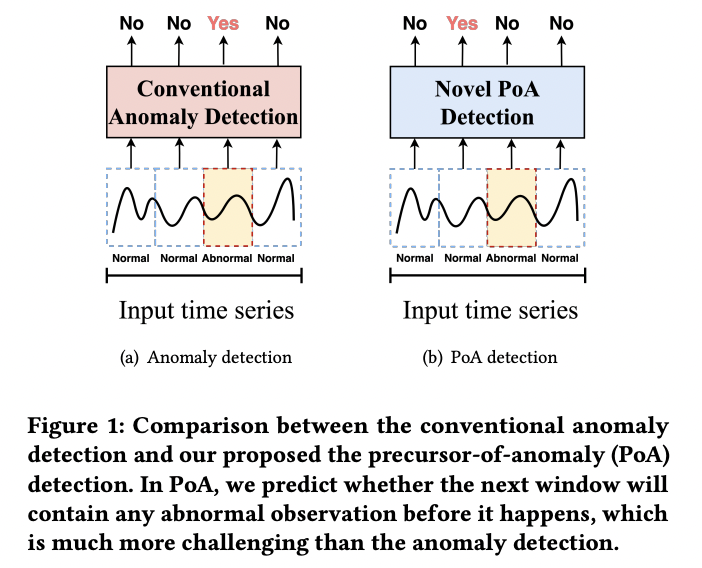
(2) Overall workflow

• (1) SSL

  • Create augmented training data

• (2) Two co-evolving NCDE layers

  • Produce the last hidden representations \(\mathbf{h}(T)\) and \(\mathbf{z}(T)\)

• (3) Training stage: Anomaly NCDE gets two inputs:

  • \(w_i\) for the anomaly detection
  • \(w_{i+1}\) for the PoA detection

• (4) Two output layers:

  • For the anomaly detection
  • For the PoA detection

  \(\rightarrow\) These two different tasks are integrated into a single training method!

  • (Multi-task learning) Shared parameter \(\theta_c\)

• (5) Two outputs:

  • Creates the two outputs \(\hat{y}_i^a\) and \(\hat{y}_{i+1}^a\) for the knowledge distillation

(3) NN based on Co-evolving NCDEs

Dual co-evolving NCDEs

• (1) One for the AD
• (2) One for PoA

[Preprocessing step]

Given a discrete TS sample \(\mathbf{x}_{1: T}\)….

\(\rightarrow\) Create a continuous path \(X(t)\) using an interpolation method

[Co-evolving NCDEs]

• Obtain two hidden vectors \(h(T)\) and \(z(T)\)
• \(\mathbf{h}(T)=\mathbf{h}(0)+\int_0^T f\left(\mathbf{h}(t) ; \theta_f, \theta_c\right) \frac{d X(t)}{d t} d t\).
• \(\mathbf{z}(T)=\mathbf{z}(0)+\int_0^T g\left(\mathbf{z}(t) ; \theta_g, \theta_c\right) \frac{d X(t)}{d t} d t\).

(Multi-task) Architecture details:

• \(f\left(\mathrm{~h}(t) ; \theta_f, \theta_e\right) =\underbrace{\rho(\mathrm{FC}(\phi(\mathrm{FC}(\mathrm{~h}(t)))))}_{\theta_f}+\underbrace{\rho(\mathrm{FC}(\phi(\mathrm{FC}(\mathrm{~h}(t)))))}_{\theta_0}\).
• \(g\left(z(t) ; \theta_g, \theta_e\right) =\underbrace{\rho(\mathrm{FC}(\phi(\mathrm{FC}(z(t)))))}_{\theta_0}+\underbrace{\rho(\mathrm{FC}(\phi(\mathrm{FC}(z(t)))))}_{\theta_0}\).
  • \(\phi\): ReLU
  • \(\beta\) : Tanh
• Note that two NCDEa co-evolve by using the shared params \(\theta_c\)

Output layers:

• (For AD) \(y_i^e=\sigma(F C_{\theta_0}(h(T))\)
• (For PoA) \(S_i^f=\sigma\left(F C_{\theta_p}(z(T))\right)\).

(4) Training Algorithm

Loss function: (CE loss)

• \(L_{K D D}=C E\left(\hat{\rho}_{i+1}^a+\hat{\rho}_{i+1}^p\right)\).
  • \(\hat{y}_{i+1}^a\) : Anomaly NCDE model’s output
  • \(\hat{y}_{i+1}^p\): PoA NCDE model’s output
• \(L_a=C E\left(\hat{y}_i^a, y_i\right)\).
  • \(y_i\): GT of anomaly detection.

4. Experiments

(1) Regular TS

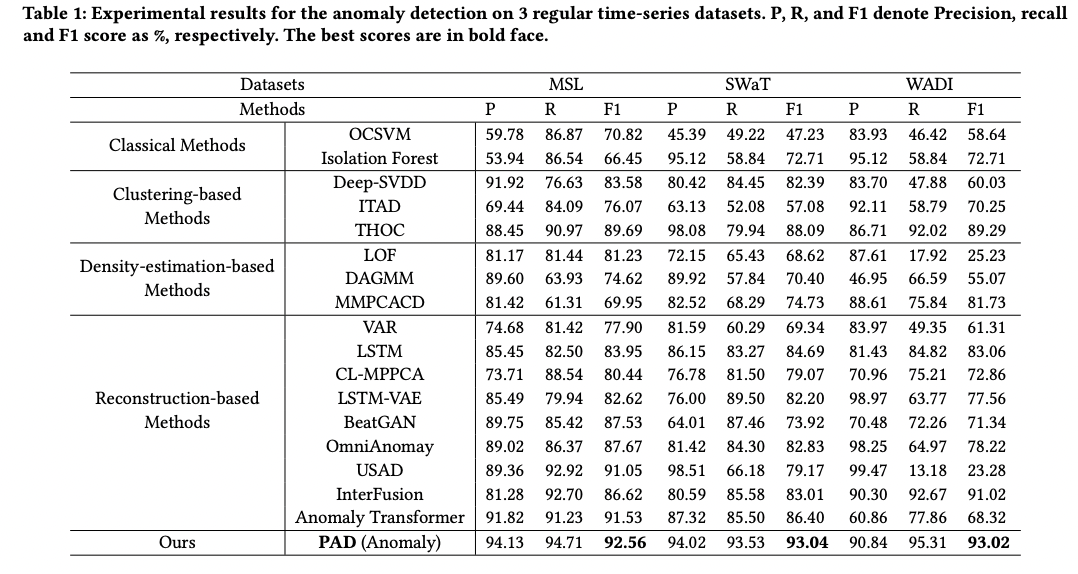
(2) Irregular TS