(paper) Learning Representations of multivariate time series with missing data

Learning Representations of multivariate time series with missing data (2019)

Contents

1. Abstract
2. Introduction
3. Methods
   1. AutoEncoder
   2. TCK (Time Series Cluster Kernel)
   3. TKAE (Temporal Kernelized Autoencoder)
   4. 도식화
4. Experiments

0. Abstract

MTS(multivariate time series)에서 compressed representation 배우기

\(\rightarrow\) 이 논문은 compressed representations of MTS를 생성하기 위한 “RNN에 긱반한 참신한 AE 구조”를 제안한다!

제안한 모델의 특징(장점)

• 1) variable lengths의 input을 받는다
• 2) missing data를 잘 다루기 위함
• 3) fixed-length vectorial representations를 학습함

1. Introduction

RNN :

• long-term dependencies를 잘 포착함
• CNN과 함께 사용되어서 다른 변수(variables)들 과의 relationship도 모델링할 수 있음

Time-series에서의 missing value

• 실생활에서 자주 발생됨

• pre-processing 단계에서 imputation으로 채워짐

  ( 하지만 MCAR이 아닌 한, imputation은 유의미한 정보들을 소실시킨다 )

Proper representation of data

• 매우 중요하다!
• (전통적 방식) domain expertise에 의해 manual하게
• (요즈음 방식) automatically produce features

Contributions

참신한 NN구조인 TKAE (Temporal Kernelized Autoencoder)를 제안함

\(\rightarrow\) “missing data”를 포함하고 있는 “real-valued MTS”의 “compressed representation”을 학습한다!

• Contribution 1 : “Learning compressed representations of MTS with missing data”

• Contribution 2 : “Frameworks for missing data imputation & anomaly detection”
  • encoder & decoder구조
  • decoder를 사용하여 imputation & reconstruction error 통한 이상치 탐지
• Contribution 3 : “Analysis of how RNNs encode MTS”

Paper Organizations

• Section 2 : 기존 AE 모델 & 제안한 TKAE 아키텍쳐 소개

• Section 3 : representation을 잘 학습하는 TKAE’s 능력

  ( 2개의 framework를 제안함 )

  • 1) impute missing data
  • 2) building a one-class classifier

• Section 4 : MTS는 AE+RNNs 구조에서 잘 작동함

2. Methods

(1) Autoencoder

• non-linear 차원축소

• 2개의 구조 : encoder & decoder

• AE의 “bottle-neck”구조가 핵심!

  • learn an “under-complete” representation

  • 자동적인 regularization 기능 ( limits the variance of the model )

  • 하지만, 추가적인 regularization 또한 사용함

    \(L=L_{r}+\lambda L_{2}=\operatorname{MSE}(\mathbf{x}, \tilde{\mathbf{x}})+\lambda \mid \mid \mathbf{W} \mid \mid _{2}^{2}\).

RNN (Recurrent NN)

• sequence내의 temporal dependencies를 잘 포착함
• seq2seq모델의 핵심
• unequal length 인풋을 받아서 fixed-size representation을 반환함

Attention

• 최근의 seq2seq구조가 많이 사용하는 메커니즘

• inductive bias를 제공함

  • to facilitate the modeling of “long-term” dependencies
  • 문장 길이가 매우 다양해도 OK

• (Time series에 적용)

  전체 문장에 대해 1개의 representation을 학습하는 대신,

  모든 encoder state를 유지 ( + combined by time-varying decoding vector at each decoding step )

(2) TCK (Time Series Cluster Kernel)

• compute unsupervised kernel similarities among MTS containing missing data
• MAR (Missing At Random) 가정 하
• GMM 앙상블 사용
• data의 local & global 구조를 모두 잘 잡아냄
• imputation을 피하기 위해, missing data는 marginalized away

TCK를 통해 어떻게 \(\mathbf{K}\)를 생성하는지는 appendix A 참고

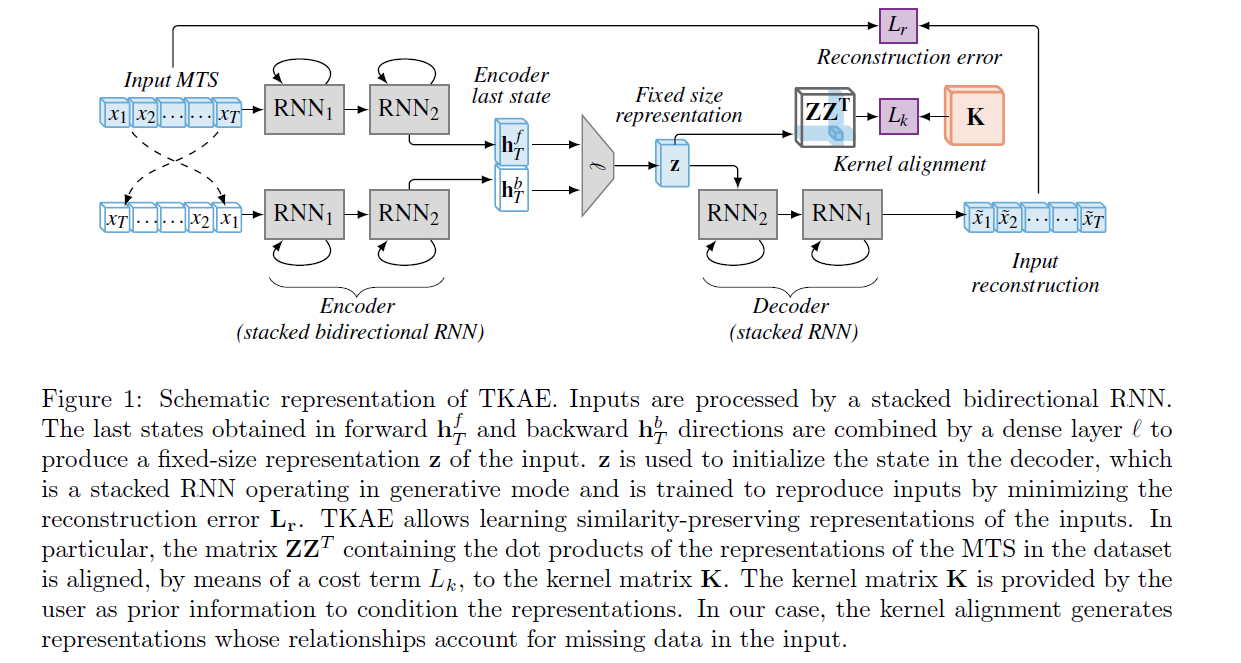
(3) TKAE (Temporal Kernelized Autoencoder)

TKAE = 이 논문에서 제안한 AE 구조

( 알고리즘 한 줄 요약 : learn compressed representations of variable-length MTS that may contain missing values )

MTS data matrix : \(\mathbf{X} \in \mathbb{R}^{V \times T}\)

• \(V\) : 변수 개수
• \(T\) : number of time steps ( 각 MTS마다 다를 수 있음 )

기존 AE의 dense layer를 RNNs로 대체함 ( LSTM, GRU 등 )

매 time step \(t\)마다의 hidden state : \(\mathbf{h}_{t}=\phi\left(\mathrm{x}_{t}, \mathbf{h}_{t-1}, \theta_{E}\right)\)

Encoding 과정

시계열 특징

• (기존) 직전 time step 이용 가능

• (시계열) whole input 가능! ( 미래 정보 input도 OK )

  \(\rightarrow\) 따라서 stacked bidirectional RNN 사용 가능 ( \(\mathbf{h}_{T}^{f}\) & \(\mathbf{h}_{T}^{b}\) 사용 )

  이 둘을 결합하여 \(\mathrm{z} \in \mathbb{R}^{D_{z}}\) 를 생성함 ( = FIXED-sized vector )

Decoding 과정

\(\tilde{\mathrm{x}}_{t}=\psi\left(\mathbf{h}_{t}, \tilde{\mathbf{x}}_{t-1}, \theta_{D}\right)\).

• \(\psi(\cdot, \cdot)\) : stacked RNN with \(M\) layers parametrized by \(\theta_{D}\)
• initial state \(\mathrm{h}_{0}=\mathrm{z}\)
• first input \(\tilde{\mathrm{x}}_{0}=0\),

Iteratively produces outputs for \(T\) steps

• \(T\) being the length of the input MTS

기타 특징

• SGD 사용하여 end-to-end 학습
• 학습 과정에서, \(t\) 시점의 input은
  • \(p_s\)의 확률로, decoder output at time \(t-1\) ( = INFERENCE mode )
  • \(1-p_{s}\)의 확률로, desired output at time \(t-1\) ( = TEACHER FORCING )

RNNs의 문제점

• directly process missing value 불가

  ( 사전에 impute 해줘야 ! with 0, mean, last observed value.. )

  \(\rightarrow\) representation의 quality 떨어짐

• 이러한 문제를 극복하기 위해, Kernel Alignment를 소개함

Kernel Alignment

• allows us to preserve the pairwise similarities of the inputs in the learned representations

• 이 pairwise similarities는 positive semi-definite matrix \(\mathbf{K}\)에 encoded 되어 있음

• additional regularization term ( \(L_{k}\) )을 사용함으로써 반영함!

  \(L=L_{r}+\lambda L_{2}+\alpha L_{k}\).

  • \(L_{k}\) : form of a normalized Frobenius norm of the difference between two matrices: \(\mathrm{K}\) and \(\mathrm{ZZ}^{T}\)

    \(L_{k}= \mid \mid \frac{\mathrm{ZZ}^{T}}{ \mid \mid \mathbf{Z Z}^{T} \mid \mid _{F}}-\frac{\mathrm{K}}{ \mid \mid \mathbf{K} \mid \mid _{F}} \mid \mid _{F}\).

  • \(\mathbf{Z} \in \mathbb{R}^{N \times D_{z}}\) : matrix of hidden representations relative to the \(N\) MTS

(4) 도식화

3. Experiments

2가지로 구성

• 1) Quantitative evaluations of the representations in the presence of missing data

  • kernel alignment의 효과를 test해봄
  • 결과 : TCK는 missing data가 많을 때 매우 효과적!

• 2) Design and evaluation of decoder-based framework

  • TKAE 디코더를 사용하여

    (1) impute missing data

    (2) one-class classification

Experiment Setup

• TKAE vs PCA / AE / RNN-based 구조
• \(D_x\) : input-dimensionality
  • TKAE ) \(D_x = V\)
  • AE / PCA ) \(D_x = V \cdot T\)
• \(D_z\) : size of compressed representations
• 3개의 hidden layer 사용 / 5000 epoch / batch size=32 / Adam optimizer

3-1) MTS representations

a) Controlled experiments & sensitivity analysis

• 목적 : kernel alignment의 효과 확인하기 : TAE (\(\alpha=0\) ) vs TKAE (\(\alpha \neq 0\) )
• 데이터 : Jp.Vow ( 원래는 missing 데이터 없어서, 10~90%로 noise 부여 )
• zero imputation

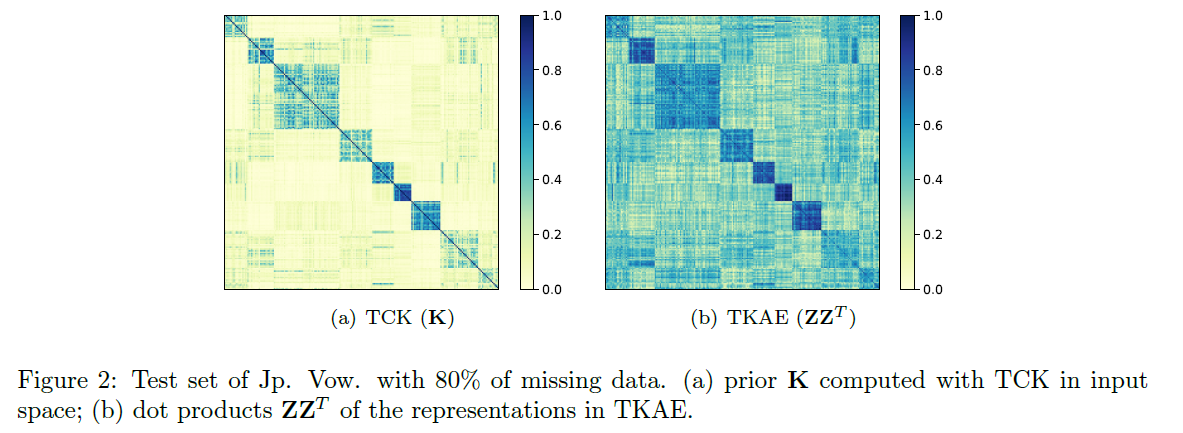
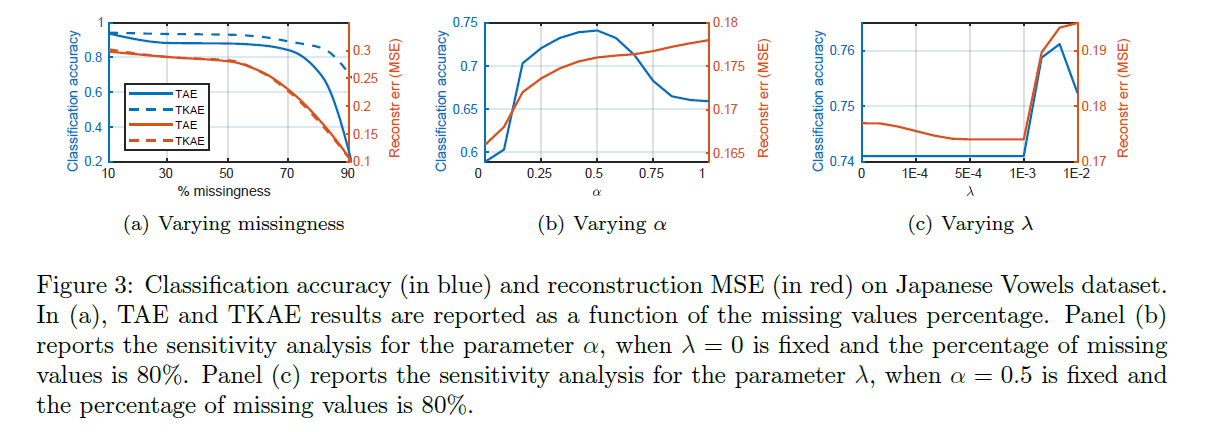
b) Classification of MTS

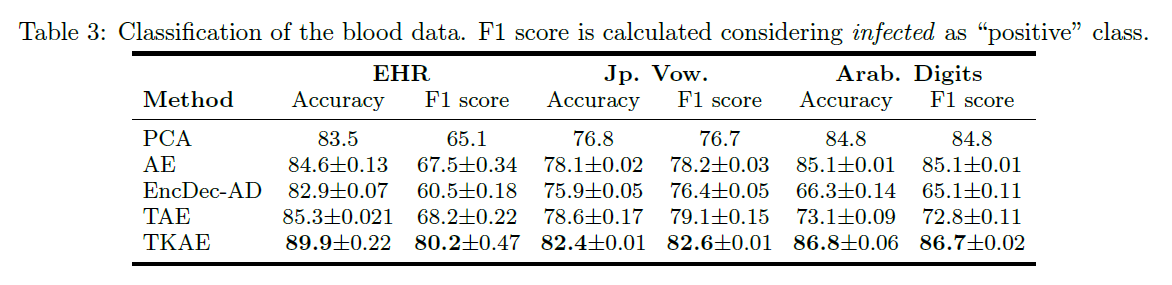
3-2) Decoder-based Frameworks

a) Imputation of missing data

reconstruction MSE

\(L_{r}=-\sum_{t}\left(\left(\mathbf{x}_{t}-\tilde{\mathbf{x}}_{t}\right) m_{t}\right)^{2} / \sum_{t} m_{t},\).

• where \(m_{t}=0\) if \(\mathrm{x}_{t}\) is imputed and 1 otherwise

b) One-class classification

• outlier개수가 너무 적을 때, 정상 데이터만 사용!
• 정상 데이터의 boundary만들고 이를 벗어나면 outlier!

4. Conclusion

TKAE 제안

• RNN-based model for representing MTS with missing values as fixed size vectors

Kernel Alignment

• time series cluster kernel
• similarity measure designed for MTS with missing data
• learn compressed representation that preserve “pairwise relationships” defined in the “original” input space

Supervised & Unsupervised task 모두 성능 good