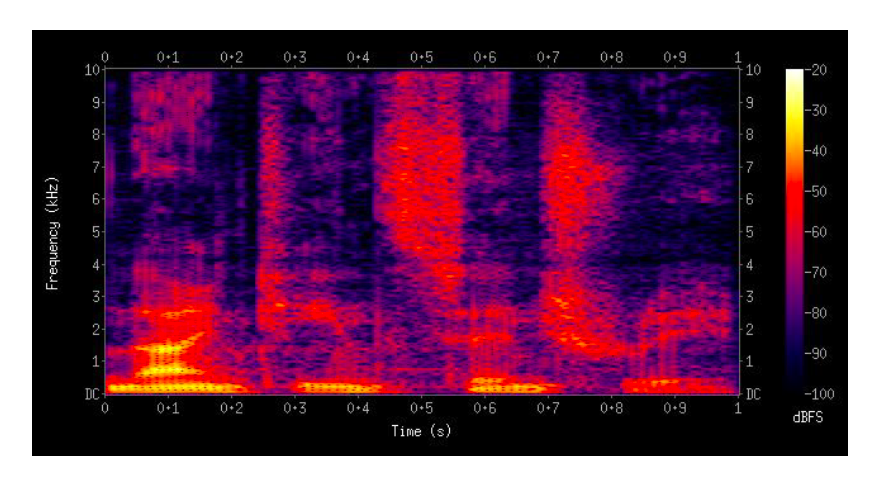
Short-Time Fourier Transform (STFT)

Short-Time Fourier Transform (STFT)

참고 : https://www.youtube.com/watch?v=fMqL5vckiU0&list=PL-wATfeyAMNrtbkCNsLcpoAyBBRJZVlnf

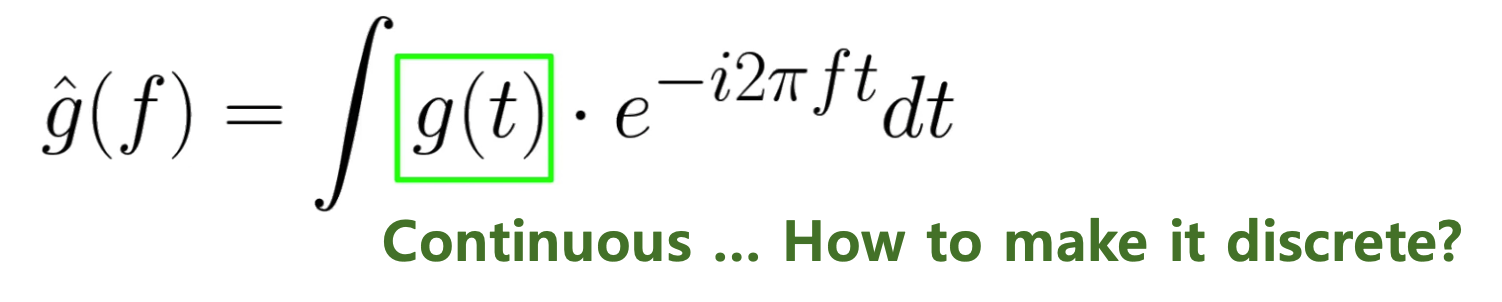
1. (Recap) Discrete Fourier Transform

\(\hat{x}(k / N)=\sum_{n=0}^{N-1} x(n) \cdot e^{-i 2 \pi n \frac{k}{N}}\).

\(\rightarrow\) no time information!

\(\rightarrow\) solution: STFT

2. STFT Intuition

slide the window & perform FFT per window!

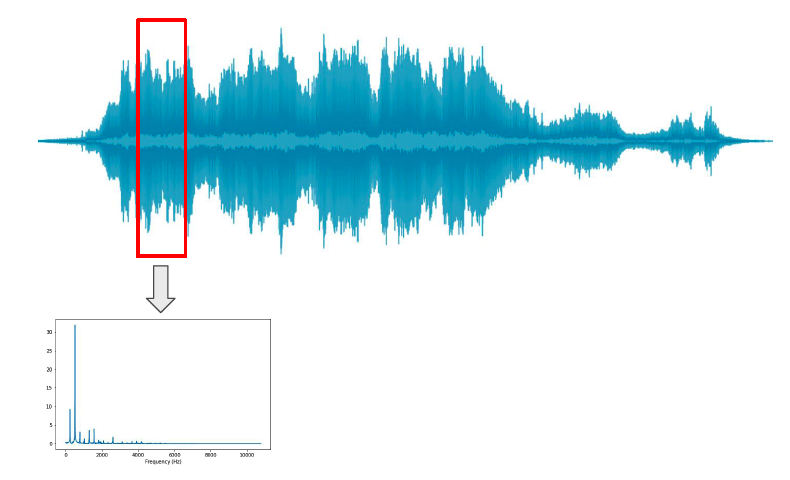
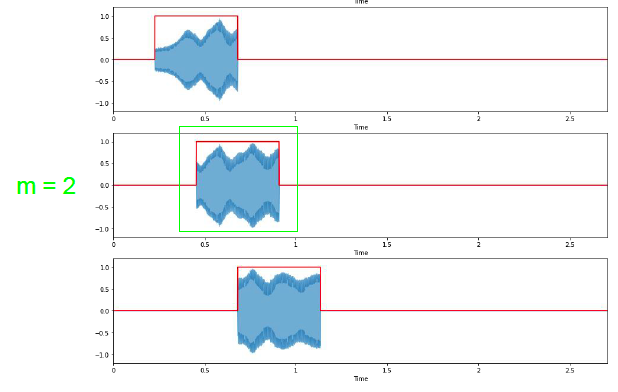
(1) Windowing

apply windowing function to signal & slide!

\(x_w(k)=x(k) \cdot w(k)\).

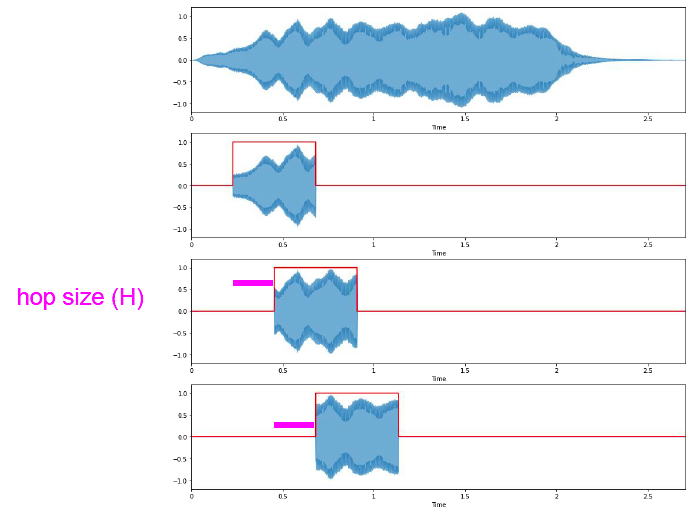
Two designs

• overlapping
• non-overlapping

(2) DFT \(\rightarrow\) STFT

[DFT]

\(\hat{x}(k)=\sum_{n=0}^{N-1} x(n) \cdot e^{-i 2 \pi n \frac{k}{N}}\).

[STFT]

\(S(m, k)=\sum_{n=0}^{N-1} x(n+m H) \cdot w(n) \cdot e^{-i 2 \pi n \frac{k}{N}}\).

• \(mH\) : starting sample of current frame

(3) Outputs

DFT

• spectral vector
  • shape: ( # of frequency bins )
• \(N\) complex Fourier coefficients

STFT

• spectral matrix
  • shape: ( # of frequency bins , # of frames)
    • # of frequency bins : \(\frac{\text{frame size}}{2} + 1\)
    • # of frames = \(\frac{N-\text{frame size}}{\text{hop size}}+1\)
• \(N^{\prime}\) complex Fourier coefficients

(4) Example

Settings

• Raw signal = 10,000 samples ( \(N=10,000\) )

• Frame size = 1,000

• Hop Size = 500

# of frequency bins = \(\frac{1000}{2}+1 = 501\) …. ( 0, sampling rate / 2)

# of frames = \(\frac{10000-1000}{500} + 1= 19\)

\(\rightarrow\) shape of spectral matrix = (501,19)

(5) Parameters of STFT

1. Frame Size
   • HIGH frame size \(\rightarrow\) HIGH frequency resolution & LOW time resolution
   • SMALL frame size \(\rightarrow\) LOW frequency resolution & HIGH time resolution
2. Hop Size
3. Windowing Function
   • ex) Hann window

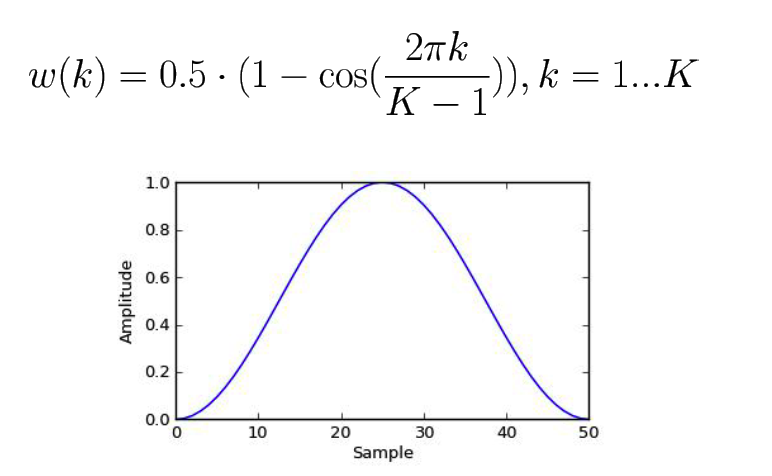
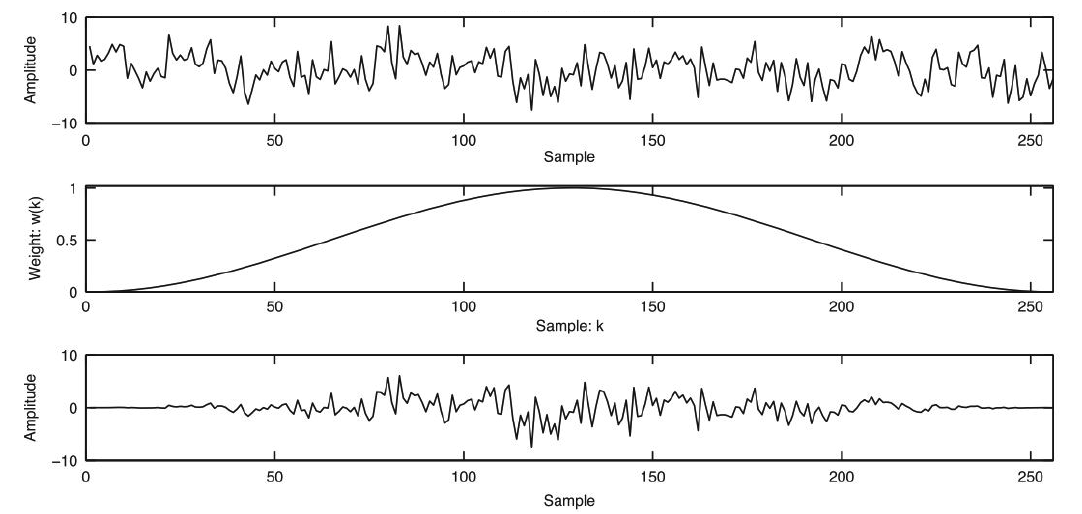
3. Spectogram

Visualizing sound

value: \(Y(m, k)=\mid S(m, k)\mid ^2\).

Spectogram