Multi-resolution Diffusion Models for Time-Series Forecasting

Multi-resolution Diffusion Models for Time-Series Forecasting

Contents

1. Abstract
2. Introduction
3. Related Works
4. Background
5. mr-Diff: Multi-Resolution Diffusion model
   1. Extracting Fine-to-Coarse Trends
   2. Temporal Multi-resolution Reconstruction
6. Experiments

0. Abstract

Diffusion model for TS

• Do not utilize the unique properties of TS data

  • TS data = Different patterns are usually exhibited at multiple scales

  \(\rightarrow\) Leverage this multi-resolution temporal structure

mr-Diff

• Multi-resolution diffusion model

• Seasonal-trend decomposition

• Sequentially extract fine-to-coarse trends from the TS for forward diffusion
  • Coarsest trend is generated first.
  • Finer details are progressively added
    • using the predicted coarser trends as condition
• Non-autoregressive manner.

1. Introduction

Multi-resolution diffusion (mr-Diff)

• Decomposes the denoising objective into several sub-objectives

Contribution

• Propose the multi-resolution diffusion (mr-Diff) model
  • First to integrate the seasonal-trend decomposition-based multi-resolution analysis into TS diffusion
• Progressive denoising in an easy-to-hard manner
  • Generate coarser signals first \(\rightarrow\) then finer details.

2. Related Works

TimeGrad (Rasul et al., 2021)

• Conditional diffusion model which predicts in an autoregressive manner
• Condition = hidden state of a RNN
• Suffers from slow inference on long TS (\(\because\) Autoregressive decoding )

CSDI (Tashiro et al., 2021)

• Non-autoregressive generation
• SSL to guide the denoising process
• Needs two transformers to capture dependencies in the channel and time dimensions

• Complexity is quadratic in the number of variables and length of TS

• Masking-based conditioning
  • cause disharmony at the boundaries between the masked and observed regions

SSSD (Alcaraz & Strodthoff, 2022)

• Reduces the computational complexity of CSDI by replacing the transformers with a SSSM
• Same masking-based conditioning as in CSDI
  • still suffers from the problem of boundary disharmony

TimeDiff (Shen & Kwok, 2023)

• Non-autoregressive diffusion model
• Future mixup and autoregressive initialization for conditioning

\(\rightarrow\) All these TS diffusion models do not leverage the multi-resolution temporal structures and denoise directly from random vectors as in standard diffusion models.

Multi-resolution analysis techniques

• Besides using seasonal-trend decomposition have also been used for TS modeling
• Yu et al. (2021)
  • propose a U-Net (Ronneberger et al., 2015) for graph-structured TS
  • leverage temporal information from different resolutions by pooling and unpooling
• Mu2ReST (Niu et al., 2022)
  • works on spatio-temporal data
  • recursively outputs predictions from coarser to finer resolutions
• Yformer (Madhusudhanan et al., 2021)
  • captures temporal dependencies by combining downscaling/upsampling with sparse attention.
• PSA-GAN (Jeha et al., 2022)
  • trains a growing U-Net
  • captures multi-resolution patterns by progressively adding trainable modules at different levels.

\(\rightarrow\) However, all these methods need to design very specific U-Net structures

3. Background

(1) DDPM

pass

(2) Conditional Diffusion Modles for TS

pass

4. mr-Diff: Multi-Resolution Diffusion Model

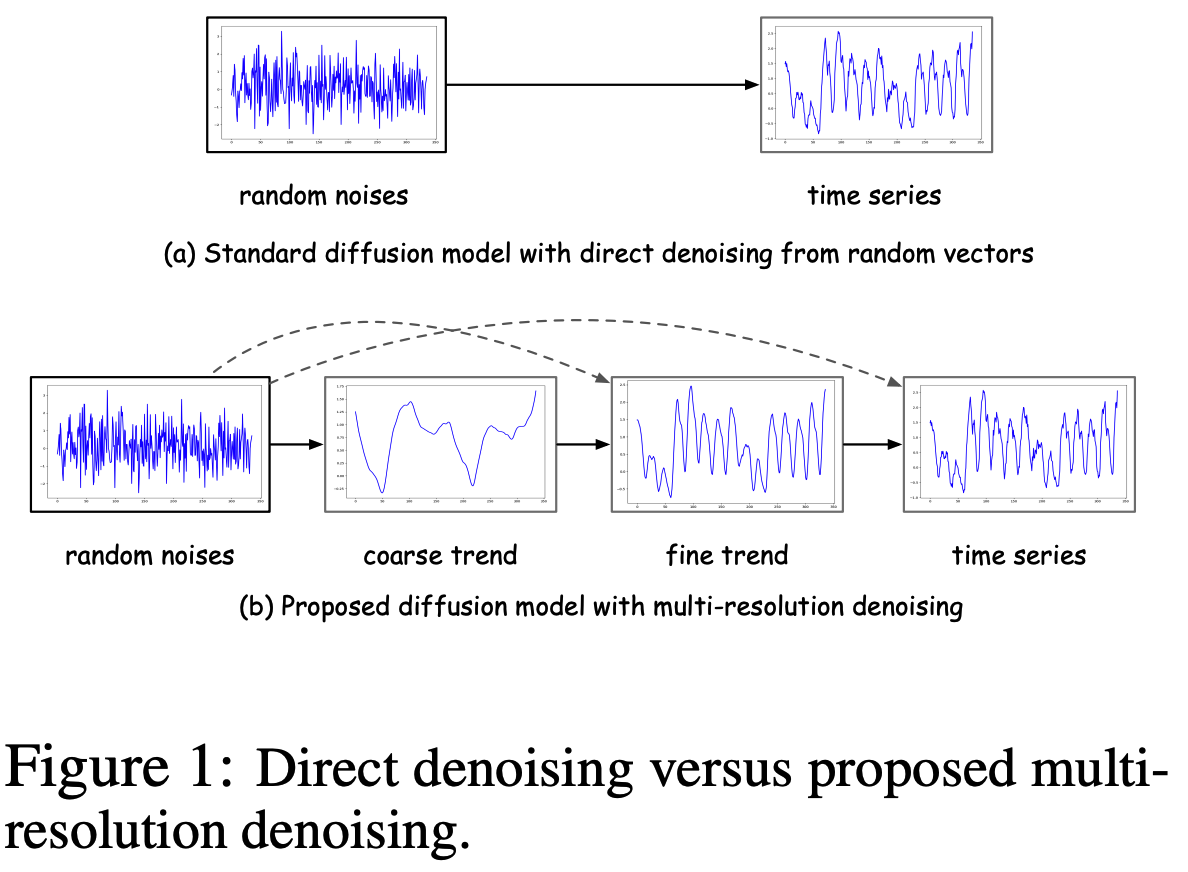
Use of multi-resolution temporal patterns in the diffusion model has yet to be explored

\(\rightarrow\) Address this gap by proposing the multi-resolution diffusion (mr-Diff)

Can be viewed as a cascaded diffusion model (Ho et al., 2022)

• Proceeds in \(S\) stages, with the resolution getting coarser as the stage proceeds

  \(\rightarrow\) Allows capturing the temporal dynamics at multiple temporal resolutions

• In each stage, the diffusion process is interleaved with seasonal-trend decomposition

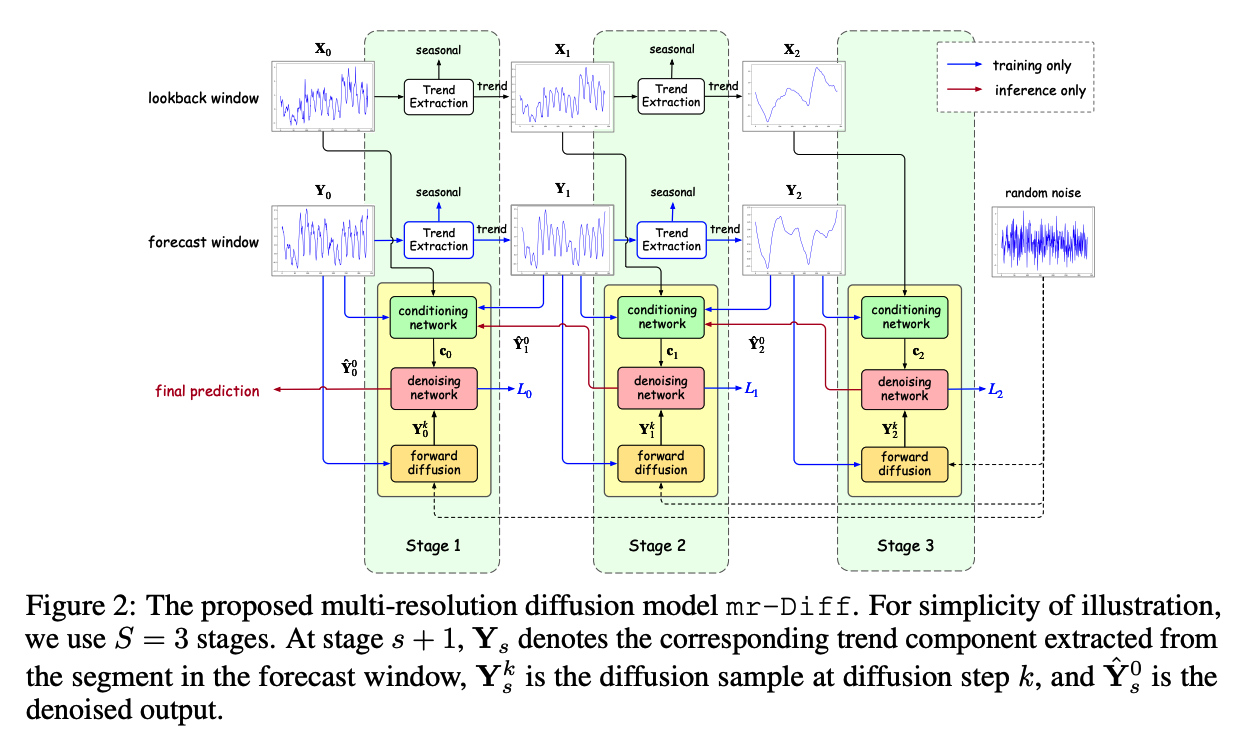
Notation

• \(\mathbf{X}=\mathbf{x}_{-L+1: 0}\) and \(\mathbf{Y}=\mathbf{x}_{1: H}\)
• Trend component of the lookback/forecast) segment at stage \(s+1\) be \(\mathbf{X}_s\) / \(\mathbf{Y}_s\)
  • Trend gets coarser as \(s\) increases
• \(\mathbf{X}_0=\mathbf{X}\) and \(\mathbf{Y}_0=\mathbf{Y}\).

In each stage \(s+1\) …

a conditional diffusion model is learned to reconstruct the “trend \(\mathbf{Y}_s\) extracted from the forecast window”

Reconstruction at stage 1 then corresponds to the target TS forecast.

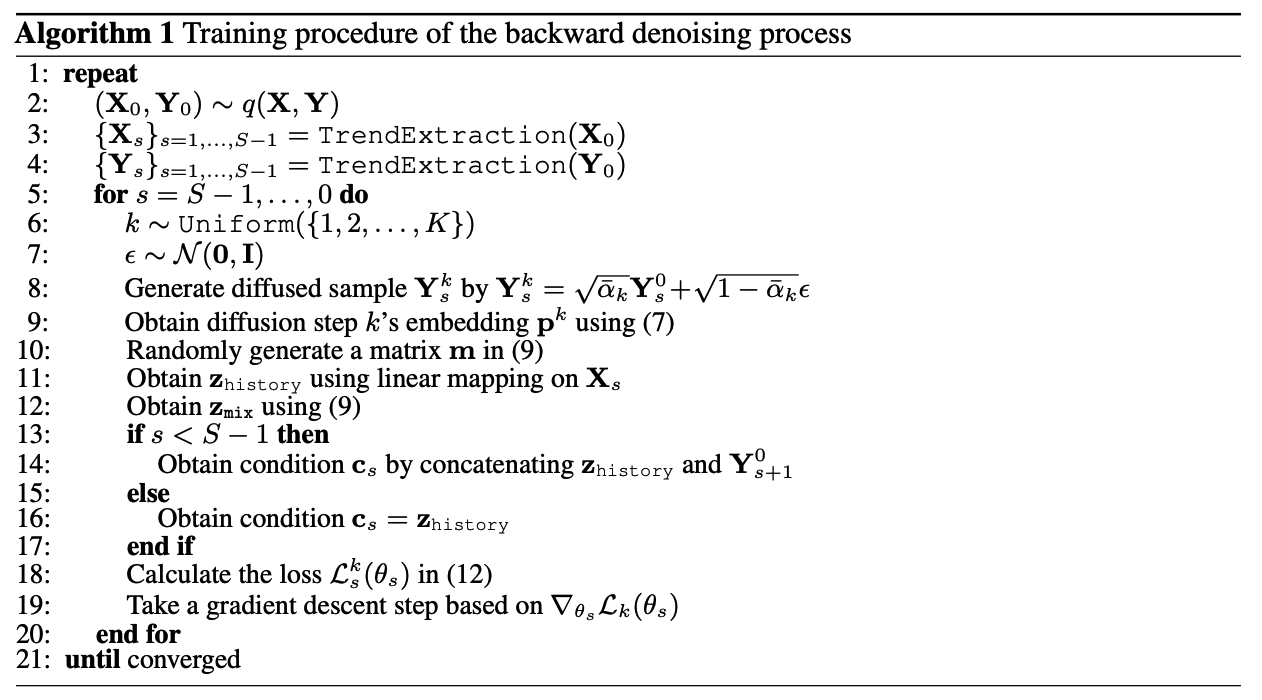
[ Training & Inference ]

Training

• Guide the reconstruction of \(\mathbf{Y}_s\)
• Condition:
  • Lookback segment \(\mathbf{X}_s\)
  • Coarser trend \(\mathbf{Y}_{s+1}\)

Inference

• Ground-truth \(\mathbf{Y}_{s+1}\) is not available
• Replaced by its estimate \(\hat{\mathbf{Y}}_{s+1}^0\) produced by the denoising process at stage \(s+1\).

(1) Extracting Fine-to-Coarse Trends

TrendExtraction module

• \(\left.\mathbf{X}_s=\text { AvgPool(Padding }\left(\mathbf{X}_{s-1}\right), \tau_s\right), s=1, \ldots, S-1\).

Seasonal-trend decomposition

• Obtains both the seasonal and trend components
• This paper focuses on trend
  • Easier to predict a finer trend from a coarser trend
  • Finer seasonal component from a coarser seasonal component may be difficult

(2) Temporal Multi-resolution Reconstruction

Sinusoidal position embedding

\(k_{\text {embedding }}=\) \(\left[\sin \left(10^{\frac{0 \times 4}{w-1}} t\right), \ldots, \sin \left(10^{\frac{w \times 4}{w-1}} t\right), \cos \left(10^{\frac{0 \times 4}{w-1}} t\right), \ldots, \cos \left(10^{\frac{w \times 4}{w-1}} t\right)\right]\)

• where \(w=\frac{d^{\prime}}{2}\),

Passing it through….

• \(\mathbf{p}^k=\operatorname{SiLU}\left(\mathrm{FC}\left(\operatorname{SiLU}\left(\mathrm{FC}\left(k_{\text {embedding }}\right)\right)\right)\right)\).

a) Forward Diffusion

\(\mathbf{Y}_s^k=\sqrt{\bar{\alpha}_k} \mathbf{Y}_s^0+\sqrt{1-\bar{\alpha}_k} \epsilon, \quad k=1, \ldots, K\).

b) Backward Denoising

Standard diffusion models

• One-stage denoising directly

mr-Diff

• Decompose the denoising objective into \(S\) sub-objectives

  \(\rightarrow\) Encourages the denoising process to proceed in an easy-to-hard manner

  ( Coarser trends first, Finer details are then progressively added )

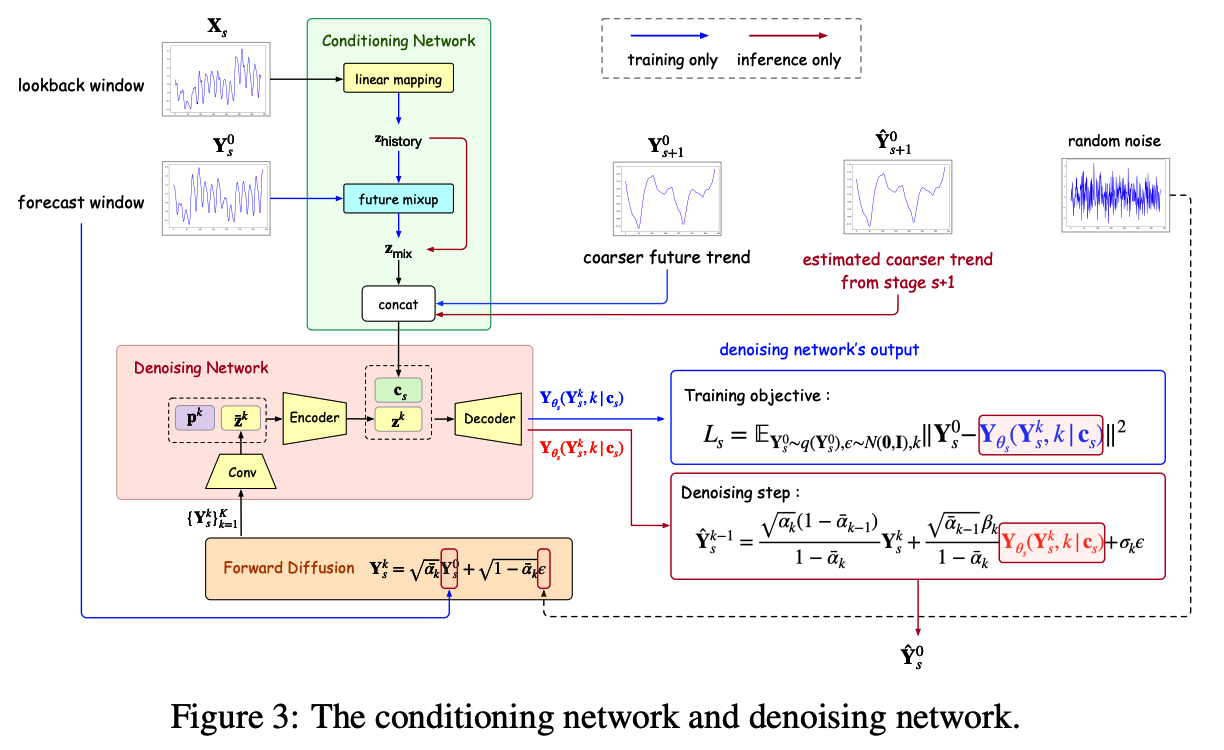
[ Conditioning network ]

Constructs a condition to guide the denoising network

Existing works

• Use the original TS lookback segment \(\mathbf{X}_0\) as condition \(\mathbf{c}\)

mr-Diff

• Use the lookback segment \(\mathbf{X}_s\) at the same decomposition stage \(s\).

  \(\rightarrow\) Allows better and easier reconstruction

  ( \(\because\) \(\mathbf{X}_s\) has the same resolution as \(\mathbf{Y}_s\) to be reconstructed )

  \(\leftrightarrow\) When \(\mathbf{X}_0\) is used as in existing TS diffusion models, the denoising network may overfit temporal details at the finer level.

Procedures

• Step 1) Linear mapping is applied on \(\mathbf{X}_s\) to produce a \(\mathbf{z}_{\text {history }} \in \mathbb{R}^{d \times H}\).

• Step 2) Future-mixup: to enhance \(\mathbf{z}_{\text {history }}\).

  • \(\mathbf{z}_{\text {mix }}=\mathbf{m} \odot \mathbf{z}_{\text {history }}+(1-\mathbf{m}) \odot \mathbf{Y}_s^0\).

  • Similar to teacher forcing, which mixes the ground truth with previous prediction output

• Step 3) Coarser trend \(\mathbf{Y}_{s+1}\left(=\mathbf{Y}_{s+1}^0\right)\) can also be useful for conditioning

  \(\rightarrow\) \(\mathbf{z}_{\operatorname{mix}}\) is concatenated with \(\mathbf{Y}_{s+1}^0\) to produce the condition \(\mathbf{c}_s\) (a \(2 d \times H\) tensor).

Inference

• Ground-truth \(\mathbf{Y}_s^0\) is no longer available

  \(\rightarrow\) No future-mixup … simply set \(\mathbf{z}_{\text {mix }}=\mathbf{z}_{\text {history }}\).

• Coarser trend \(\mathbf{Y}_{s+1}\) is also not available

  \(\rightarrow\) Concatenate \(\mathbf{z}_{\text {mix }}\) with the estimate \(\hat{\mathbf{Y}}_{s+1}^0\) generated from stage \(s+2\) .

[ Denoising Network ]

Outputs a \(\mathbf{Y}_{\theta_s}\left(\mathbf{Y}_s^k, k \mid \mathbf{c}_s\right)\) with guidance from the condition \(\mathbf{c}_s\)

Denoising process at step \(k\) of stage \(s+1\):

• \(p_{\theta_s}\left(\mathbf{Y}_s^{k-1} \mid \mathbf{Y}_s^k, \mathbf{c}_s\right)=\mathcal{N}\left(\mathbf{Y}_s^{k-1} ; \mu_{\theta_s}\left(\mathbf{Y}_s^k, k \mid \mathbf{c}_s, \sigma_k^2 \mathbf{I}\right)\right), k=K, \ldots, 1\).

• \(\mathbf{Y}_{\theta_s}\left(\mathbf{Y}_s^k, k \mid \mathbf{c}_s\right)\) is an estimate of \(\mathbf{Y}_s^0\).

Procedures

• Step 1) Maps \(\mathbf{Y}_s^k\) to the embedding \(\overline{\mathbf{z}}^k \in \mathbb{R}^{d^{\prime} \times H}\)
• Step 2) Concatenate with diffusion-step \(k\) ‘s embedding \(\mathbf{p}^k \in \mathbb{R}^{d^{\prime}}\)
• Step 3) Feed to an encoder to obtain the \(\mathbf{z}^k \in \mathbb{R}^{d^{\prime \prime} \times H}\).
• Step 4) Concatenate \(\mathbf{z}^k\) and \(\mathbf{c}_s\) along the variable dimension
  • Form a tensor of size \(\left(2 d+d^{\prime \prime}\right) \times H\).
• Step 5) Feed to a decoder
  • Outputs \(\mathbf{Y}_{\theta_s}\left(\mathbf{Y}_s^k, k \mid \mathbf{c}_s\right)\).

Loss function:

• \(\min _{\theta_s} \mathcal{L}_s\left(\theta_s\right)=\min _{\theta_s} \mathbb{E}_{\mathbf{Y}_s^0 \sim q\left(\mathbf{Y}_s\right), \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I}), k} \mid \mid \mathbf{Y}_s^0-\mathbf{Y}_{\theta_s}\left(\mathbf{Y}_s^k, k \mid \mathbf{c}_s\right) \mid \mid ^2\).

Inference

• For each \(s=S, \ldots, 1\), we start from \(\hat{\mathbf{Y}}_s^K \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)
• Each denoising step from \(\hat{\mathbf{Y}}_s^k\) (an estimate of \(\mathbf{Y}_s^k\) ) to \(\hat{\mathbf{Y}}_s^{k-1}\) :
  • \(\hat{\mathbf{Y}}_s^{k-1}=\frac{\sqrt{\alpha_k}\left(1-\bar{\alpha}_{k-1}\right)}{1-\bar{\alpha}_k} \hat{\mathbf{Y}}_s^k+\frac{\sqrt{\bar{\alpha}_{k-1}} \beta_k}{1-\bar{\alpha}_k} \mathbf{Y}_{\theta_s}\left(\hat{\mathbf{Y}}_s^k, k \mid \mathbf{c}_s\right)+\sigma_k \epsilon\).

Pseudocode

5. Experiments

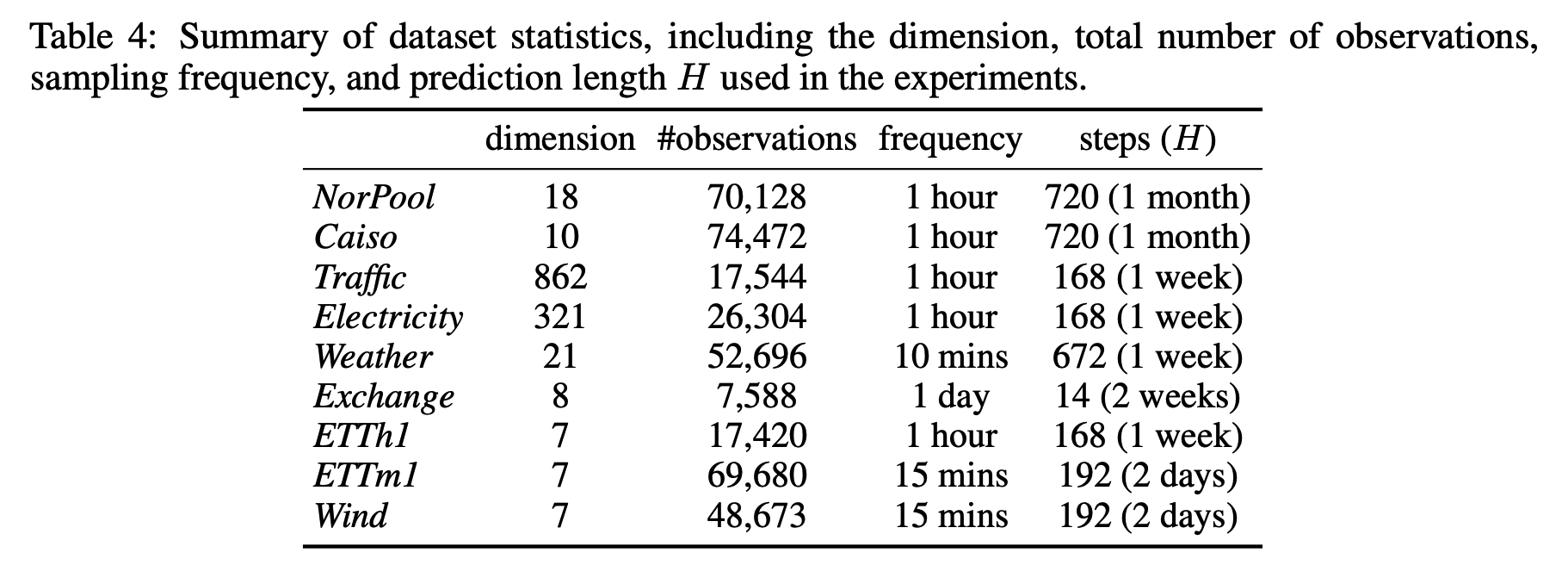
22 recent strong prediction models

9 popular real-world time series datasets

a) Performance Measures

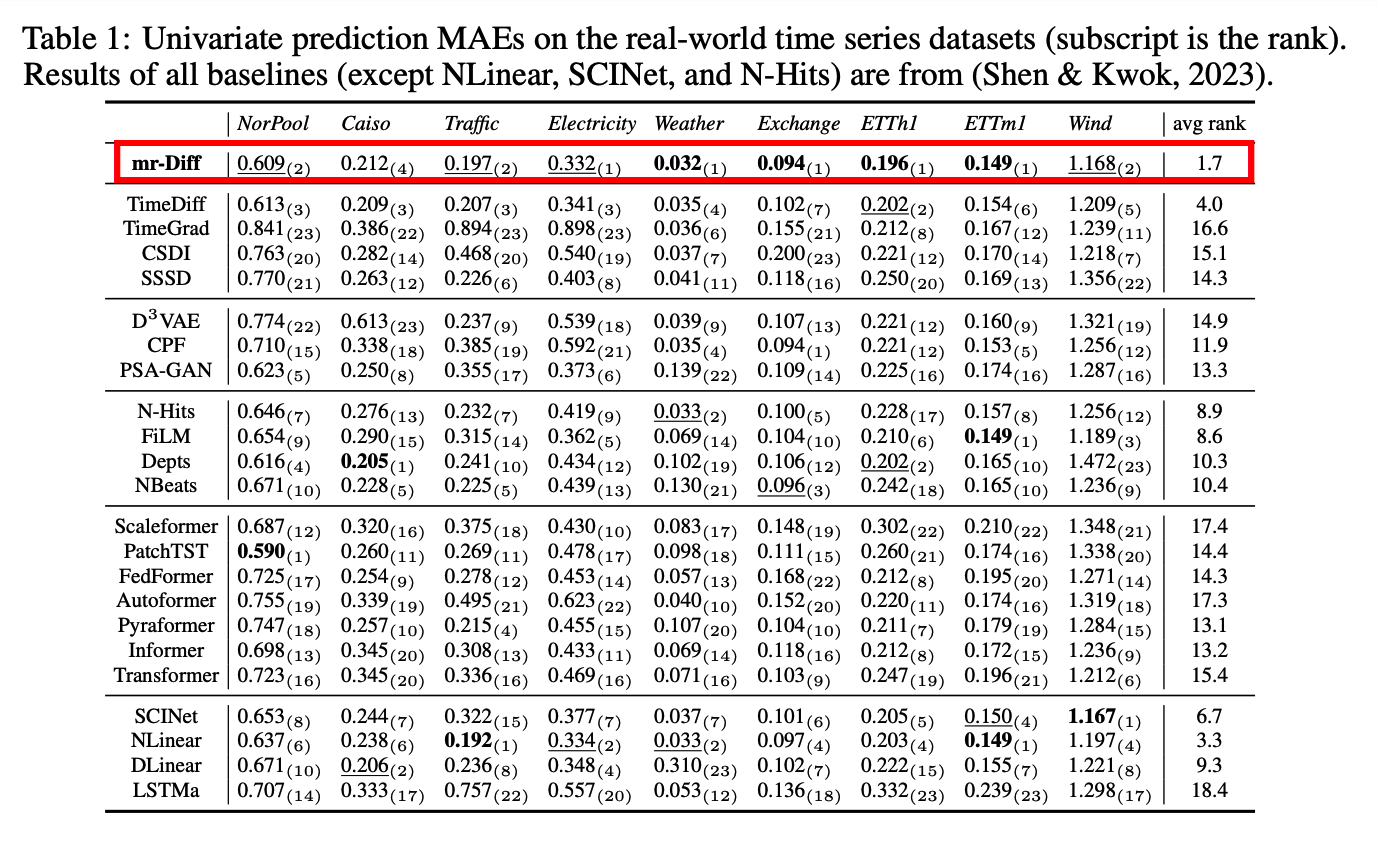
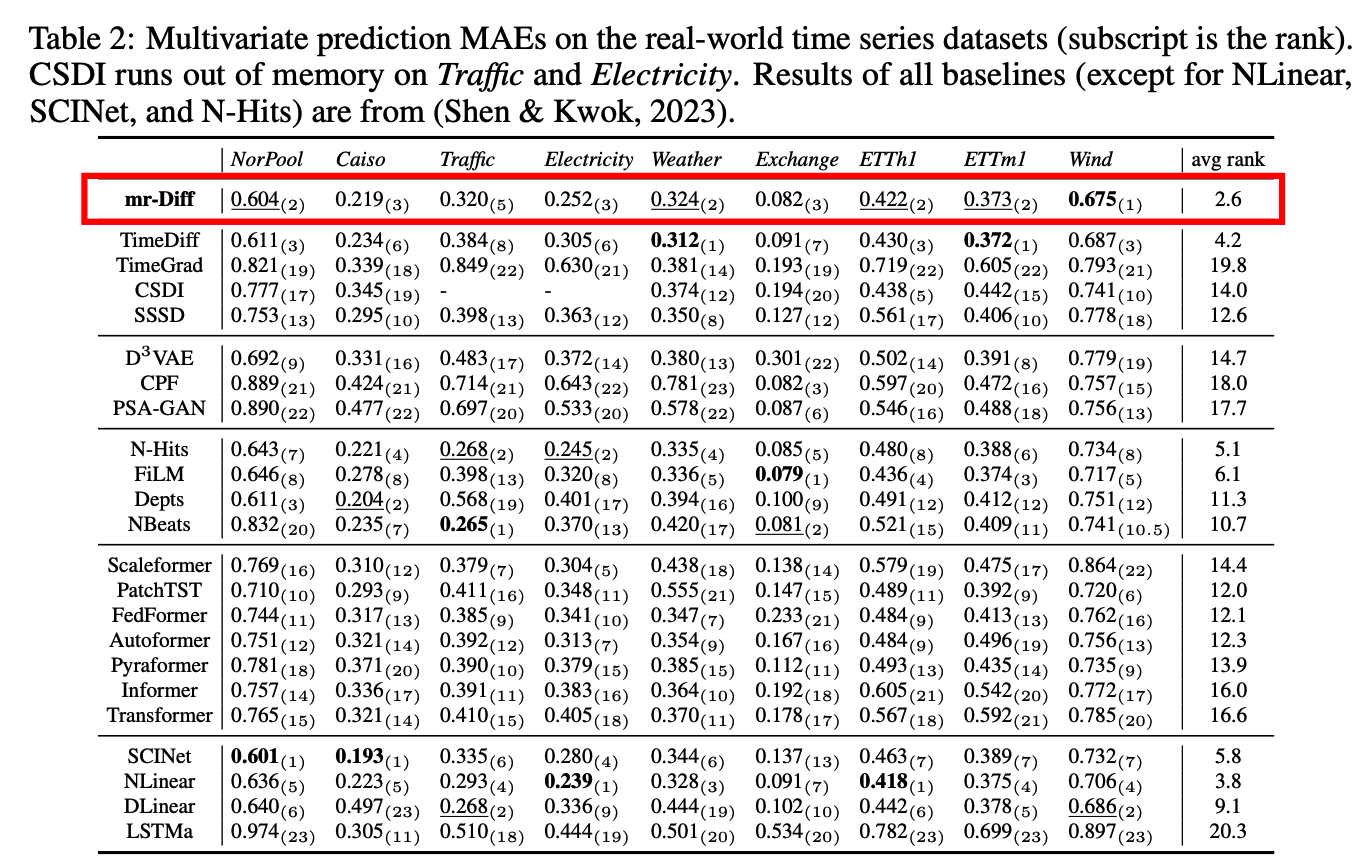
• mean absolute error (MAE)

• mean squared error (MSE)

  ( results on MSE are in Appendix K )

b) Implementation Details

• Adam with a learning rate of \(10^{-3}\).
• Batch size is 64
• Early stopping for a maximum of 100 epochs.
• \(K=100\) diffusion steps are used
  • with a linear variance schedule (Rasul et al., 2021) starting from \(\beta_1=10^{-4}\) to \(\beta_K=10^{-1}\)
• \(S=5\) stages
• History length (in \(\{96,192,336,720,1440\}\) )
  • is selected by using the validation set

(1) Main Results

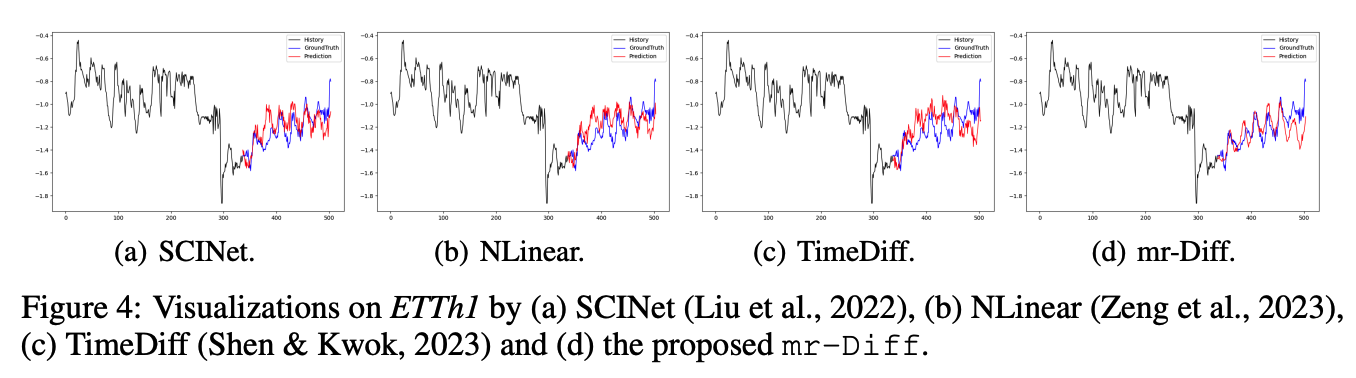
(2) Inference Efficiency