C-Mamba; Channel Correlation Enhanced State Space Models for Multivariate Time Series Forecasting via Factorized Temporal and Channel Mixing

C-Mamba: Channel Correlation Enhanced State Space Models for Multivariate Time Series Forecasting

Contents

1. Abstract
2. Introduction
3. Preliminray
   1. MTS forecasting
   2. Mamba
4. Methodology
   1. Channel Mixup
   2. C-Mamba Block
5. Experiments

0. Abstract

Limitations of previous models

• Linear: limit in capacities
• Attention: quadratic complexity
• CNN: restricted receptive field

CI strategy: ignoring their correlations!!

CD strategy: considering inter-channel relationships

• Via self-attention mechanism, linear combination, or convolution …

  \(\rightarrow\) high computational costs

C-Mamba

• (1) SSM that captures (2) cross-channel dependencies ,

  while maintaining (3) linear complexity (4)without losing the global receptive field

• Components

  • (1) Channel mixup
    • two channels are mixed to enhance the training sets
  • (2) Channel attention enhanced patch-wise Mamba encoder
    • leverages the ability of the SSM
    • capture cross-time dependencies and models correlations between channels by mining their weight relationships.

1. Introduction

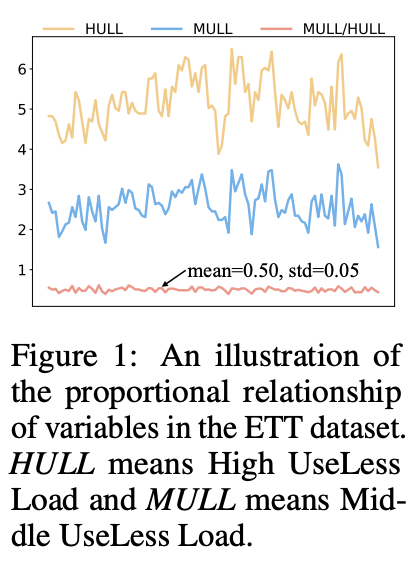
Cross-channel dependencies are also vital for MTSF!

Ex) two variables over time in the ETT

Observations:

• (1) Two variables exhibit strong temporal characteristics similarity

• (2) Show a strong proportional relationship

  • MULL (Middle UseLess Load) = 1/2 x HULL (High UseLess Load)

    \(\rightarrow\) Necessity of modeling cross-channel dependencies from proportional relationships

C-Mamba

• To better capture cross-time and cross-channel dependencies

• Channel enhanced SSM

• Problem & Solution [1]

  • Problem) Oversmoothing caused by the CD

  • Solution) Channel mixup strategy

    • inspired by mixup data augmentation

    • fuses two channels via a linear combination for training

      ( = generate virtual channel )

    • Generate virtual channel integrate characteristics from different channels while retaining their shared cross-time dependencies, which is expected to improve the generalizability of models.

• Problem & Solution [2]

  • Problem) Capturing both cross-time and cross-channel dependencies
  • Solution) Channel attention enhanced patch-wise Mamba encoder
    • a) Cross-time dependencies: via Mamba ( + Patching )
      • Patch-wise Mamba module
    • b) Cross-channel dependencies: via channel attention
      • Lightweight mechanism that considers various relationships between channels
        • (1) weighted summation relationships & (2) proportional relationships

2. Preliminary

(1) MTS forecasting

Notation

• \(\mathbf{X}=\left\{\mathbf{x}_1, \ldots, \mathbf{x}_L\right\} \in \mathbb{R}^{L \times V}\) ,
  • \(\mathbf{X}_{t,:}\) : value of all channels at time step \(t\),
  • \(\mathbf{X}_{:, v}\) as the entire sequence of the channel indexed by \(v\)
• \(\mathbf{Y}=\left\{\mathbf{x}_{L+1}, \ldots, \mathbf{x}_{L+T}\right\} \in \mathbb{R}^{T \times V}\).

(2) Mamba

Notation

• Input \(\mathbf{x}(t) \in \mathbb{R}\),
• Output \(\mathbf{y}(t) \in \mathbb{R}\),
• Hidden state \(\mathbf{h}(t) \in \mathbb{R}^N\)

\(\begin{aligned} \mathbf{h}^{\prime}(t) & =\mathbf{A h}(t)+\mathbf{B x}(t), \\ \mathbf{y}(t) & =\mathbf{C h}(t), \end{aligned}\).

• \(\mathbf{A} \in \mathbb{R}^{N \times N}\) : state transition matrix,
• \(\mathbf{B} \in \mathbb{R}^{N \times 1}\) and \(\mathbf{C} \in \mathbb{R}^{1 \times N}\) : projection matrices

Multivariate TS

• \(\mathbf{x}(t) \in \mathbb{R}^V\) and \(\mathbf{y}(t) \in \mathbb{R}^V\),
• \(\mathbf{A} \in \mathbb{R}^{V \times N \times N}, \mathbf{B} \in \mathbb{R}^{V \times N}\), \(\mathbf{C} \in \mathbb{R}^{V \times N}\).
  • \(\mathbf{A}\) can be compressed to \(V \times N\)

Discreticize

\(\begin{aligned} \overline{\mathbf{A}} & =\exp (\Delta \mathbf{A}) \\ \overline{\mathbf{B}} & =(\Delta \mathbf{A})^{-1}(\exp (\Delta \mathbf{A})-\mathbf{I}) \Delta \mathbf{B} \\ \mathbf{h}_t & =\overline{\mathbf{A}} \mathbf{h}_{t-1}+\overline{\mathbf{B}} \mathbf{x}_t \\ \mathbf{y}_t & =\mathbf{C h}_t \end{aligned}\).

• where \(\Delta \in \mathbb{R}^V\) is the sampling time interval

Global convolution

\(\begin{aligned} & \overline{\mathbf{K}}=\left(\mathbf{C} \overline{\mathbf{B}}, \mathbf{C A B}, \ldots, \mathbf{C} \overline{\mathbf{A}}^{L-1} \overline{\mathbf{B}}\right) \\ & \mathbf{Y}=\mathbf{X} * \overline{\mathbf{K}}, \end{aligned}\).

• where \(L\) is the length of the sequence.

Selective scan mechanism

Selective scan strategy ( Data-dependent mechanism )

• \(\mathbf{B} \in \mathbb{R}^{L \times V \times N}, \mathbf{C} \in \mathbb{R}^{L \times V \times N}\),
• \(\Delta \in \mathbb{R}^{L \times V}\) : derived from the input \(\mathbf{X} \in \mathbb{R}^{L \times V}\).

3. Methodology

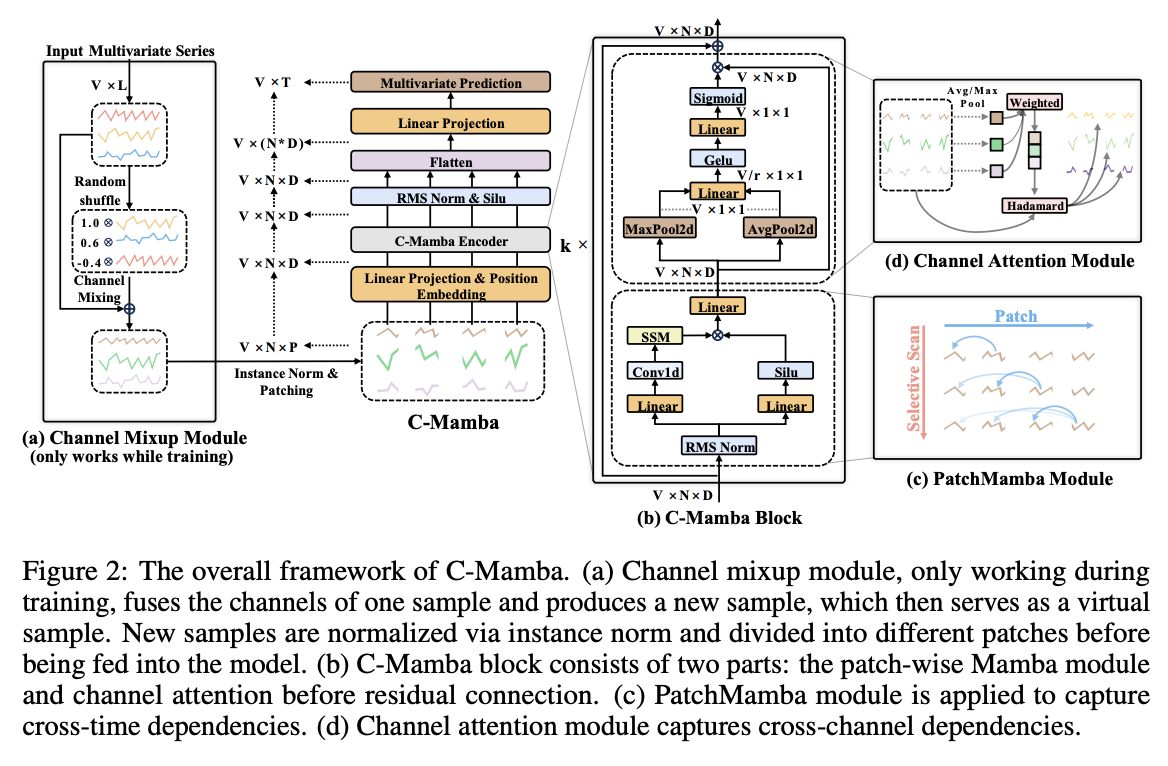
Before training

• Channel mixup module: Mixes MTS in channel dim

Model

• C-Mamba block
  • Vanilla Mamba module
  • Channel attention module
• Exploits both cross-time and cross-channel dependencies.
• Patch-wise sequences

(1) Channel Mixup

Mixup

\(\begin{aligned} & \tilde{x}=\lambda x_i+(1-\lambda) x_j \\ & \tilde{y}=\lambda y_i+(1-\lambda) y_j \end{aligned}\).

• where \((\tilde{x}, \tilde{y})\) is the synthesized virtual sample, and \(\lambda \in[0,1]\).

Channel Mixup

\(\begin{aligned} & \mathbf{X}^{\prime}=\mathbf{X}_{:, i}+\lambda \mathbf{X}_{:, j}, i, j=0, \ldots, V-1 \\ & \mathbf{Y}^{\prime}=\mathbf{Y}_{:, i}+\lambda \mathbf{Y}_{:, j}, i, j=0, \ldots, V-1 \end{aligned}\).

• where \(\mathbf{X}^{\prime} \in \mathbb{R}^{L \times 1}\) and \(\mathbf{Y}^{\prime} \in \mathbb{R}^{T \times 1}\) are hybrid channels
• where randperm \((V)\) generates a randomly arranged array of \(0 \sim V-1\)
• \(\lambda \sim N\left(0, \sigma^2\right)\) is the linear combination coefficient

Normal distribution with a mean of 0

\(\rightarrow\) Ensuring that the overall characteristics of each channel remain unchanged.

(2) C-Mamba Block

Consists of two key components:

• (1) Patch-wise Mamba module
• (2) Channel attention module

\(\rightarrow\) Capture cross-time and cross-channel dependencies respectively!

a) PatchMamba

Patching

• Each univariate TS \(\mathbf{X}_{: v} \in \mathbb{R}^L\),
• \(\hat{\mathbf{X}}_{: v}=\operatorname{Patching}\left(\mathbf{X}_{: v}\right) \in \mathbb{R}^{N \times P}\).

b) Channel Attention

Structure of the channel attention module.

Notation:

• \(\mathbf{H}_l \in \mathbb{R}^{V \times N \times D}\): Embedding after the \(l^{t h}\) PatchMamba module

• \(\operatorname{Att}_l=\operatorname{sigmoid}\left(\operatorname{MLP}\left(\operatorname{MaxPool}\left(\mathbf{H}_l\right)\right)+\operatorname{MLP}\left(\operatorname{AvgPool}\left(\mathbf{H}_l\right)\right)\right)\).

  • AvgPool and MaxPool : applied to the last two dimensions

• \(\operatorname{Att}_l=\operatorname{sigmoid}\left(\mathbf{W}_1\left(\operatorname{Gelu}\left(\mathbf{W}_0 \mathbf{F}_{\text {max }}^l\right)\right)+\mathbf{W}_1\left(\operatorname{Gelu}\left(\mathbf{W}_0 \mathbf{F}_{\text {avg }}^l\right)\right)\right)\).

  • \(\mathbf{F}_{\text {max }}^l \in \mathbb{R}^{V \times 1 \times 1}\) and \(\mathbf{F}_{\text {avg }}^l \in \mathbb{R}^{V \times 1 \times 1}\) ,

  • \(\mathbf{W}_0 \in \mathbb{R}^{V / r \times V}\) and \(\mathbf{W}_1 \in \mathbb{R}^{V \times V / r}\),

    • \(r\): controlling the parameter complexity, denotes the reduction ratio.

      ( = Essential for time series with hundreds of channels, tune it in \(\{2,4,8\}\). )

• \(\operatorname{Att}_l \in \mathbb{R}^{V \times 1 \times 1}\):

\(\mathbf{C A}_l=\operatorname{Att}_l \odot \mathbf{H}_l .\) : output of the channel attention module

c) Overall Pipeline

(Instance normalization to mitigate the distribution shifts)

• \(\mathbf{X}^{\prime}, \mathbf{Y}^{\prime}=\operatorname{Mixup}(\mathbf{X}, \mathbf{Y})\).

• \(\mathbf{X}_{\text {norm }}^{\prime}=\operatorname{InstanceNorm}\left(\mathbf{X}^{\prime}\right)\).

• \(\hat{\mathbf{X}} =\operatorname{Patching}\left(\mathbf{X}_{\text {norm }}^{\prime}\right)\).

• \(\mathbf{Z}_0 =\hat{\mathbf{X}} \mathbf{W}_p+\mathbf{W}_{\text {pos }}\).

  • learnable position encoding \(\mathbf{W}_{\text {pos }}\).

  • where \(\hat{\mathbf{X}} \in \mathbb{R}^{V \times N \times P}, \mathbf{W}_p \in \mathbb{R}^{P \times D}, \mathbf{W}_{\text {pos }} \in \mathbb{R}^{N \times D}\), and \(\mathbf{Z}_0 \in \mathbb{R}^{V \times N \times D}\)

[C-mamba encoder .. k blocks]

• \(\begin{aligned} \mathbf{H}_l & =\operatorname{PatchMamba}\left(\mathbf{Z}_{l-1}\right), \\ \mathbf{Z}_l & =\operatorname{Att}_l\left(\mathbf{H}_l\right) \odot \mathbf{H}_l+\mathbf{Z}_{l-1} \end{aligned}\).

• \(\hat{\mathbf{Y}}_p=\operatorname{Flatten}\left(\operatorname{Silu}\left(\operatorname{RMS}\left(\mathbf{Z}_k\right)\right)\right) \mathbf{W}_{p r o j}\).

  • linear projection layer: \(\mathbf{W}_{p r o j} \in \mathbf{R}^{(N * D) \times T}\)
  • \(\hat{\mathbf{Y}}_p \in \mathbb{R}^{V \times T}\).

4. Experiments