DTMamba; Dual Twin Mamba for Time Series Forecasting

DTMamba : Dual Twin Mamba for Time Series Forecasting

Contents

1. Introduction
2. Proposed Method
   1. Problem Statement
   2. Normalization
   3. CI & Reverse CI
   4. Twin Mamba
3. Experiments

1. Introduction

DTMamba (Dual Twin Mamba)

[Procedure]

• RevIN
  • CI layer
    • TMamba blocks (\(\times 2\))
    • Projection layer
  • revese CI
• reverse RevIN

2. Proposed Method

Three layers

• (1) CI layer
• (2) TMamba block
  • embedding
  • FC layer
  • dropout
  • pair of twin Mambas
• (3) Projection layer

(1) Problem Statement

Multivariate TS

\(X=\left\{x_1, \ldots, x_L\right\}\).

• \(X_i \in \mathbb{R}^N\) consists of \(N\) dimensions \(\left\{x_i^1, \ldots, x_i^N\right\}\)

TS forecasting

• \(X=\left\{x_1, \ldots, x_T\right\} \in\) \(\mathbb{R}^{T \times N}\),
• \(\hat{X}=\left\{\hat{x}_{T+1}, \ldots, \hat{x}_{T+S}\right\} \in \mathbb{R}^{S \times N}\) ,

(2) Normalization

\(X^0=\left\{x_1^0, \ldots, x_T^0\right\} \in \mathbb{R}^{T \times N}\), via \(X^0=\operatorname{RevIN}(X)\).

(3) CI & Reverse CI

(B,T,N) \(\rightarrow\) (BxN, 1, T)

(4) Twin Mamba

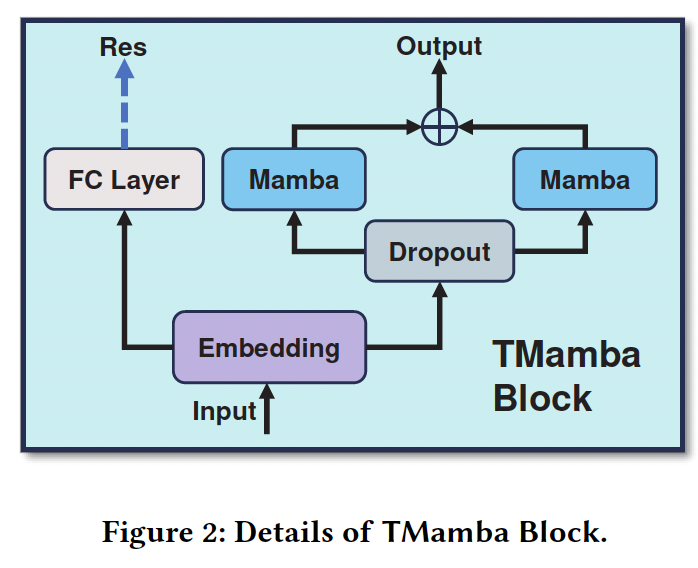
a) Embedding Layes

Embed the \(X^I\) into \(X^E:(B \times\) \(N, 1, n i)\).

DTMamba

• consists of two TMamba Block in total

Embedding layer

• Embed the TS into \(\mathrm{n} 1\) and \(\mathrm{n} 2\) dimension
  • Embedding 1 & Embedding 2

b) Residual

• To prevent overfitting
• FC layer to change the dimension of the residual

c) Dropout

\(X^E\) \(\rightarrow\) \(X^D:(B \times N, 1, n i)\).

d) MAMBAs

TMamba Block = Two parallel Mamba.

• Multi-level feature learning can be achieved.

• Mamba (1)
  • learn low-level temporal features
• Mamba (2)
  • learn high-level temporal patterns

e) Projection Layer

\(R^1\) and \(R^2\)

• Representation learned by the two pairs of TMamba Block

Step 1) Addition operation

• \(X^A:(B \times N, 1, n 2) \leftarrow X^I+R^1+R^2\).

Step 2) Prediction ( next length \(S\) )

• Use a linear layer
• Get \(X^P:(B \times N, 1, S)\),

Step 3) Reverse CI ( = reshape )

• \(\hat{X}:(B, S, N)\).

3. Experiments